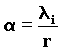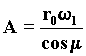As explained above, the term added to the G.R. can become more and more determining as we experiment with deviations of photons with masses giving out spherical fields of waves composed by waves that are still close to their source of elementary waves.

These waves still have a very small radius, and therefore can interact with light, determining the greatest possible angle of deviation for any photons crossing the geometry of the space-time established by their presence.

This happens when the relationship between the wavelength of the incident photon and the radius of the resonance orbit crossed by a wave, approaches the unit. In such a case, the first part of the general relativity formula loses importance and can be totally neglected, while the added term becomes predominant:

60)

Let’s consider that the angle of deviation of the photon is greater than the angles normally experimented in the Compton effect or that it is at least:a = 2p.

Let’s explain how can we reach such a deviation after passing through several wave situations, by using an electron having l_e, as a wavelength.
This electron is invested by a photon having l_i = l_e/2, as a wavelenght diverting it by an angle a = 2p: 

1) The Relative Symmetry Principle pushes the electron to the  v₁,velocity, since the photon transfers half of its momentum to it. The photon, running after the electron, loses half of its momentum because of the Doppler effect, and its wavelength becomes l_i1 = l_e.

2) Let’s consider that the resultant photon is continuously diffracted by the field of spherical waves of the electron, completing another deviation equals to 180°, returning to its original position.

3) The photon-wave train rotates on a circular orbit in a closed circuit, round the source of the field of spherical waves of the electron, completing an angle of 360°.

4) if the length of the closed circuit crossed by the photon is equal to the final wavelength of the photon, the wave train is subject to the waves resonance law, which perpetuates the motion of the wave on the resonance orbit:

61)

5) When n = 1, the wave train, that has already completed a revolution, can complete more reolutions, superimposing all the wavefronts to the first one, that had already placed itself in a resonance condition, on the orbit having r₀ as a radius.

Considering the whole wavefront, which tries to place itself in a resonance condition, only the part that is closest to the center of the deviant spherical wave field is able to place itself with one or more elementary surfaces, in the resonance condition.
The rest of the L² elementary wavefronts constituting the wavefront is propagated on the paths depending on conditions of curvature imposed by the spherical waves of the field of wave belonging to the obstacle particle, that is an electron or a proton.

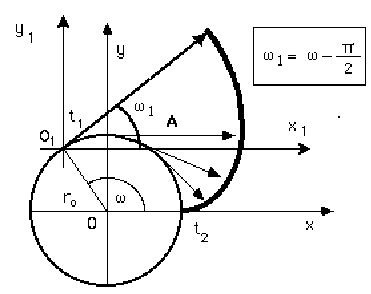
The diffracted wavefront is deformed, during its propagation, in the Schild space-time, and places itself according to a characteristic surface known as: Sperical Involvent or Spherical Involute.

The points intersected by the Spherical Involvent on the plane containing the resonance orbit enable us to describe the plane Involute curve that, according to a x y frame of reference having its origin in the center of the resonance orbit, and to a x₁, y₁, frame of reference which is parallel to the first one and rotates with the c velocity on the orbit, can be described by:

On the resonance orbit identified by the Involvent, an A vector rotates with an increasing c velocity, going from the  t₂ to the t₁ time describing the E curve appeared in the t₁ time. The Involvent produces wavefronts that are more and more approximately circular to the distances compared to which r becomes a negligible quantity, and it maintains the l₀ wavelength constant.

It can also be bidimensionally described in an exponential form by the A vector given that:

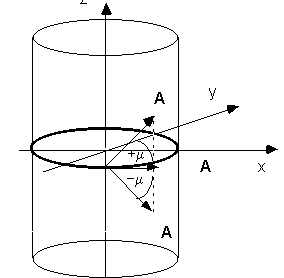
65)

We now can tridimensionally deal with the developments of the model, by ideally projecting in the z axis of the resonance orbit the orbit itself, so as to obtain a half positive and half negative infinite ideal cylinder.

Let’s consider the set of the A vectors for a fan-shaped direction variation until reaching the ±m angle.

In order to make the surface of the Involute spherical we displace the A vector, according to the temporal properties of the Schild lattice.
The values of this vector, in a Riemannian cylindrical geometry coincide with the surface of the cylinder and have at least a 2m.

Given that l₀ = 2pr₀, we are able to describe the helicoid as a geodesic, that starting from the resonance orbit twines round the ideal cylinder, which is constituted by the projection of the resonance orbit.

Its modulus is given by:

There are two helicoids: one for m that develops from a point of the resonance orbit towards the positive z; the other, that is the mirror image of the first one, develops for  m that is propagated towards the negative z. For m = ±p/4 we have:

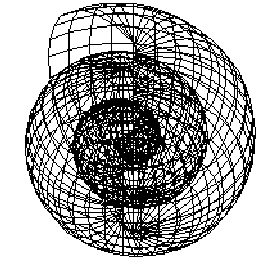
The spherical link of the helicoids with the involvent curve constitutes a surface that, during its evolution, forms the Spherical Involvent.

This is the Spherical Involvent we identify with an elementary particle-rest source of waves, having  m₀ as a mass.

69)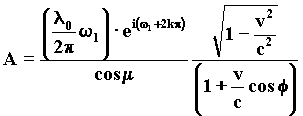

 

The formula show the secret of the material micro-universe.

The wave-particle.

As shown in the figure, the meridians appear perpendicular to the plane of the resonance orbit, but in reality (we’ll explain it when we speak about the justification of charges), they are inclined and  like two screw threads they twine round the spherical surface.

A simple Basic program show the structure of the wave-particle: Basic-involvent.htm

The first one on the right-hand side and the other one, its mirror image, on the left-hand one (the parallels and meridians don't exist but at the level of the elementary dimensions of the Schild space-time).

We now have the data we can use to describe the Spherical Involvent and its dynamics, so as to establish a connection between the behaviour of the particle-source of waves and the relativistic variation of the waves of the Spherical Involvent and identify it with the particle itself.