|
Leonardo von Pisa , bekannt unter dem Namen Fibonacci stellte im
Liber Abbaci folgendes Problem "aus dem Liebesleben der Kaninchen" dar:
Es wird die Nachkommenschaft eines (idealisierten) Kaninchenpaares unter folgenden Annahmen betrachtet:
Dies führt zu der Rekursionsformel: a 1 =1, a 2 =1, a n+2 =a n+1 +a n Und ergibt folgende Zahlenfolge, auch Fibonacci-Zahlen genannt: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ... Betrachtet man nun jene durch die Fibonacci-Zahlen definierte Folge z n = z =
also nach Multiplikation mit z:
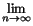 z n = z n =
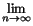 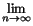 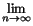 (1 + (1 + = 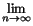 (1 + (1 + 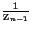 ) = 1 + ) = 1 +
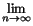 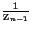 = 1 + = 1 +
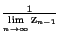 = (1 + = (1 +  ) ) z 2 = z + 1
oder:
z 2 - z - 1 = 0
Dies ist genau die algebraische Gleichung, die wir schon bei der Berechnung des goldenen Schnittes
gelöst haben mit der einzigen positiven Lösung 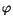 = = . .
Da nun z n = 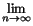 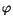 = =  . .
|