How to "play" the interactive model:

Click and drag to rotate the 3d object. Roll over (or click) a sphere to make it sound. Or, press any three adjacent keys on you keyboard to make a chord. Press "space" to stop all ringing notes. Also, you can switch between views (3d/2d views) to get a different look at your songs. Sustain toggles sustain on and off. Don't expect to play complex melodies on this instrument; it is designed for playing and finding harmonies.

Using the Sequencer:

The underlying idea:

figure 1

For a real life analogy, consider the arrangement of objects in a supermarket. Ideally, items which are used together frequently are placed closer together in space. Salsa is usually sitting next to chips. A supermarket roughly arranges objects on a 3d continuum. In the above lattice, tones are mapped-out with respect to harmony.

The lattice is a repeating pattern; tones on any edge are the same as those on the opposite edge. To form a simple 3d model, imagine rolling the shape into a tube, and then bending the tube into a donut shape. As a donut (or torus), there are no redundant tones represented in the model. (Also, this surface can be generalized in order to represent octaves. Since this is just an overview, I wont go into that.)

For what it is worth, here is the java source code I wrote to measure the occurance of tone combinations in ordinary midi files. The results of these tests, overall, support the assumptions of this theory. For example:

the first number in each row is the musical interval (mod 12).
the second number is the percentage of time the interval is used in the music.
the line '¤¤¤¤¤¤¤' is just to see the percentage as a bar

input file: yesterday.mid

3:   11%  ¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤
4:   7%   ¤¤¤¤¤¤¤¤¤¤¤¤¤¤
5:   6%   ¤¤¤¤¤¤¤¤¤¤¤¤
7:   6%   ¤¤¤¤¤¤¤¤¤¤¤¤
9:   5%   ¤¤¤¤¤¤¤¤¤¤
0:   5%   ¤¤¤¤¤¤¤¤¤¤
2:   3%   ¤¤¤¤¤¤
10:  3%   ¤¤¤¤¤¤
8:   2%   ¤¤¤¤
6:   1%   ¤¤
11:  1%   ¤¤
1:   1%   ¤¤

36713 total song slices measured

A few important properties of the model... Every triangle pointing upward is a major triad.

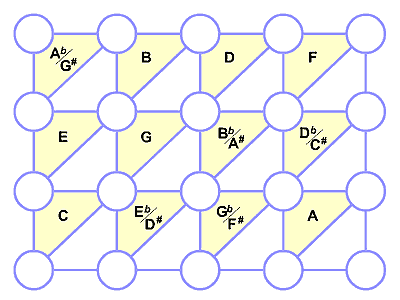
figure 2

Every triangle pointing downward is a minor triad.

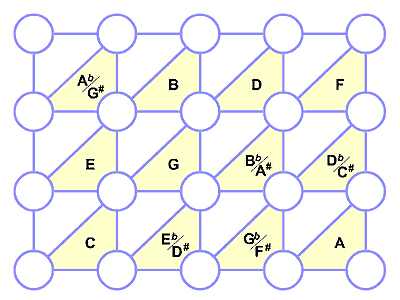
figure 3

Vertical bars form augmented chords.

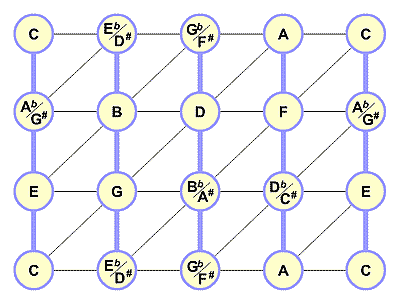
figure 4

Horizontal bars form diminished chords.

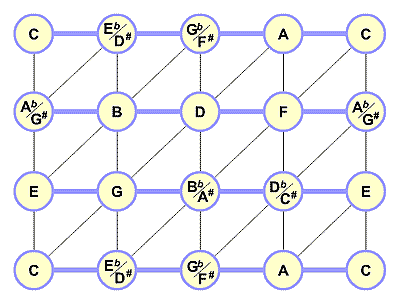
figure 5

Most other chords can be formed from simple combinations and/or fragments of the above.

The "do re me..." diatonic scale is formed by taking a diagonal slice of notes. Shown here is the key of Bb (g minor).

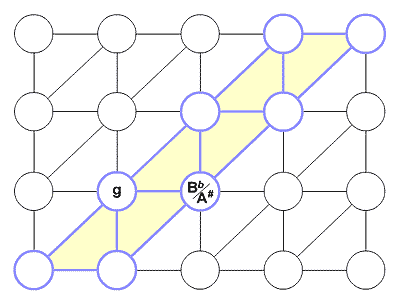
figure 6

Of course, how can we apply all this? Here's a very simple example. Suppose that we have a 2 note melody.

figure 7

Now let's harmonize it. There's actually a lot of choices here. Even with the most rudimentary harmony, you have a choice of 3 major triads, 3 minor triads, 1 diminished and 1 augmented chord, for any melody note. So, for a 2 note melody, you could easily have 64 different possible harmonizations.

However, by visualizing the problem, one can see 64 possible harmonizations at a glance. We simply pick an orange and blue triangle that sound good. Or any line intersecting with the melody notes. If you want to stay within a key, keep within the diagonal lines.

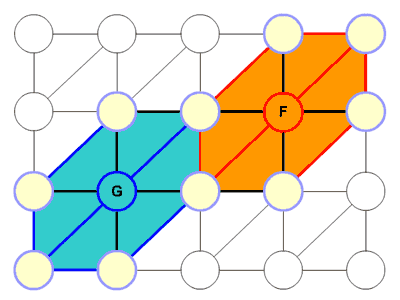
figure 8

Of course, this model is not meant to be restrictive. The ear always has the final say. But hopfully it will help narrow the search for good harmonies, and maybe inspire new songwriting ideas by looking at the problem from another perspective. The model can be used to describe how harmonies are formed, how chords hook together, and how chords and melodies move. Further generalizations, though, are beyond the scope of this paper. You may notice more patterns as you play with the interactive demo. Enjoy!

Troubleshooting interactive model:

I don't see anything. You may need to download and install the latest Flash plugin to view the interactive model.

This site is best when viewed with Microsoft Internet Explorer 4+, or Netscape Navigator 4.