Appendix A Select Matrix Algebra
Here are some select matrix algebra related to the dissertation. For
detailed results, please refer to Appendix M (Searle et al., 1992),
Chapters 15 and 16 (Harville, 1997) and Chapters 7 and 8 (Schott, 1997). Some unconventional results not found in the literature but used in the dissertation are given in Lemmas.
A.1 Special Matrices and Operators
A.1.1 Matrix Element-Wise Notations
These compact notations are from Appendix M.3 (Searle et al., 1992). It is especially helpful in algebraic simplifications when typical elements are easily specified, but naming each matrix is not needed. Under most circumstances of incomplete data, the direct element-wise operation is usually desired, and these notations just serve that purpose very well.
Familiar notation for a matrix A of order p × q is A = {aij} or (aij), where aij is the element that is in the ith row and jth column of A for i = 1, ..., p and j = 1, ..., q. We abbreviate this to
A = {m aij}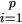 ,
, 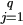 = {m aij}i,j
= {m aij},
= {m aij}i,j
= {m aij},
using m to indicate that the elements inside the braces are being arrayed as a matrix; and sufficient detail of subscripts follows the braces as is necessary, depending on context. For diagonal matrix, indicate with letter d as follows,
| A = | 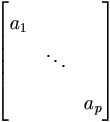 |
= {d ai}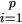 = {d ai}. = {d ai}. |
For row and column vectors, use r and c respectively. Let u = (u1, u2, ..., up), then
u = {r ui}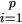 = {r ui},
and u' = {c ui}
= {r ui},
and u' = {c ui}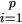 = {c ui}.
= {c ui}.
Extension to partitioned matrices is straightforward, for example,
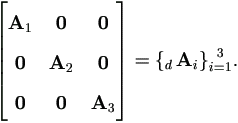
And it can also used in a nested manner, for example,
yi = {c yij}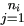 , and
y = {c yi}
, and
y = {c yi}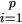 = {c {c yij}
= {c {c yij}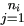 }
}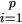 .
.
A.1.2 The Direct Product
For matrices A = (aij)m×n and Br×s, the direct product (also called the Kronecker product) of A and B is a matrix of order mr × ns defined as
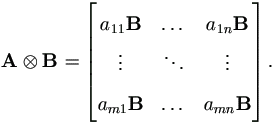
In particular, Im In = Imn.
For more than two matrices,
In = Imn.
For more than two matrices,
A  B
B  C
= A
C
= A  (B
(B  C)
= (A
C)
= (A  B)
B)  C,
C,
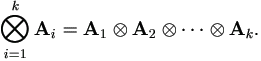
Some useful properties of direct products follow.
- For a being a scalar: a
 A = A
A = A  a = aA.
a = aA.
- For x and y being vectors:
x'
 y = y
y = y  x' =yx'.
x' =yx'.
- In transposing, (A
 B)'= A'
B)'= A'  B'.
B'.
- For A and B being nonsingular square matrices,
(A
 B)-1 = A-1
B)-1 = A-1  B-1.
B-1.
- Given conformability of regular matrix multiplication,
(A  B)(X B)(X  Y) = (AX) Y) = (AX)  (BY). (BY). |
(A.1) |
- For partitioned matrices, [ A1 A2 ]
 B
= [ A1
B
= [ A1 B A2
B A2 B ].
B ].
- Rank and trace, rA
 B
= rA rB and
tr(A
B
= rA rB and
tr(A  B) = tr(A) tr(B).
B) = tr(A) tr(B).
- For A and B being square matrices,
|Am×m
 Bn×n| = |A| n |B| m.
Bn×n| = |A| n |B| m.
The matrix operator vec(X) creates a column vector from the columns of matrix A by locating them one under the
other. For a matrix X = {r xj}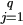 of order p×q, define vec(X) = {c xj}
of order p×q, define vec(X) = {c xj}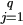 of order
pq×1. For example,
of order
pq×1. For example,
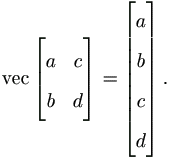
A very useful property of operator vec is with matrix trace,
| tr(AB) = (vec A')' vec B. | (A.2) |
Relationship with Direct Product
vec A = (Im  A) vec Im. A) vec Im. | (A.3) |
In general, the following relationship is very useful,
vec(ABC) = (C'  A) vec(B). A) vec(B). | (A.4) |
Apply it to the inverse of a nonsingular matrix A-1 = A-1AA-1, then
vec(A-1)
= (A'-1  A-1) vec(A)
= (A' A-1) vec(A)
= (A'  A)-1 vec(A). A)-1 vec(A).
| (A.5) |
The following useful results can be verified easily.
Lemma A.1 For vectors an×1 and bm×1,
a  b = vec(ba') = (In b = vec(ba') = (In b)a. b)a. |
(A.6) |
Proof.
Directly comparing elements in both sides gives the first part; and
the second part is due to equation (A.1) as a  b
= (In
b
= (In b)(a
b)(a  1)
= (In
1)
= (In b) a.
b) a.
Lemma A.2 For vectors a and b,
vec(a'  b) = a b) = a  b. b. | (A.7) |
Proof. This is due to the property (2) of direct product and the prior Lemma.
Special Matrix Pm,k,n
This matrix is used in Chapter 4, which moves vec in and out of a matrix. Define the constant matrix Pm,k,n as
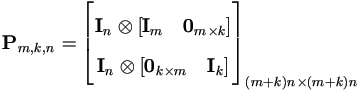 | (A.8) |
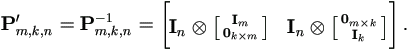 | (A.9) |
This matrix is very useful in the context of vec due to the following properties.
Lemma A.3 For matrices Am×n and Bk×n with same number of columns,
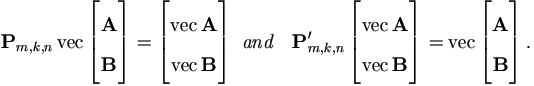 | (A.10) |
This property can be verified directly using column vectors of A and B. Due to (A.3), the following equation is more general. For matrices Am×r and Bk×r with same number of columns, and any matrix Cn×s,
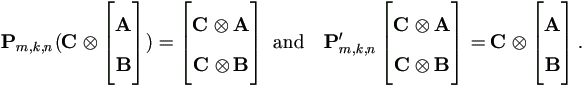 | (A.11) |
Or for matrices Ar×m and Br×k with same number of rows and any matrix Cs×n,
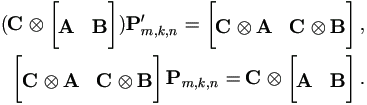 | (A.12) |
Some classical useful results regarding to vector and matrix differentiation are briefly listed in this section. For detailed results, please refer to Appendix M.7 (Searle et al., 1992), Chapter 15 (Harville, 1997) and Chapter 8 (Schott, 1997). Some results not found in the literature but used in the dissertation are given in Lemmas.
A.2.1 Scalars and Vectors
Differentiation with Scalars
Let λ be a scalar and vector xq×1. Define
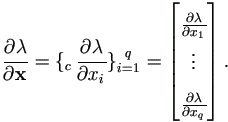
If scalar y is a function of matrix X, and matrix A = (aij) is a function y, define
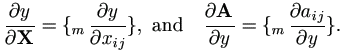
For a being unrelated to x,
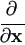 (a'x) =
(a'x) = 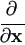 (x'a) = a,
and
(x'a) = a,
and
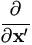 (a'x) =
(a'x) = 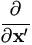 (x'a) = a'.
(x'a) = a'.
Differentiation with Vectors
Suppose vector yp×1 is a differentiable function of vector xq×1. Define
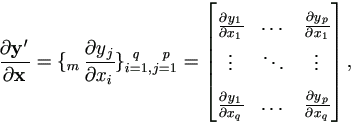 | (A.13) |
a matrix of order q×p. Its transpose is a matrix of order p×q as
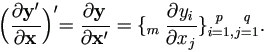
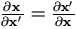 . For matrices A and B being not functions of x,
. For matrices A and B being not functions of x,
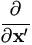 (Ax) = A and (Ax) = A and 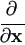 (x'B) = B. (x'B) = B. | (A.14) |
The Chain Rule
For vector x,y,z, the chain rule is,
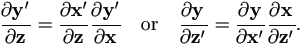 | (A.15) |
Matrix With Respect To All Elements
For vector an×1 not function of matrix Xn×m,
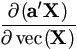 = Im = Im a and a and
 = a = a  Im. Im. |
(A.16) |
 | (A.17) |
A.2.2 Products and Quadratic Forms
Products
Suppose p×1 vectors u and v are differentiable functions of vector x,
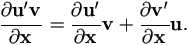 | (A.18) |
If A and B are matrices and t is a scalar, it is easy to verify
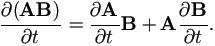 | (A.19) |
Lemma A.4 Suppose matrix A and vector b are differentiable functions of vector tp×1, then
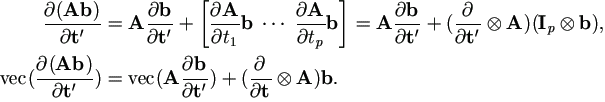 | (A.20) |
Proof.
Since  and by (A.19), easy to have the first equation. The second simply re-arranges the first and reflects the fact
and by (A.19), easy to have the first equation. The second simply re-arranges the first and reflects the fact
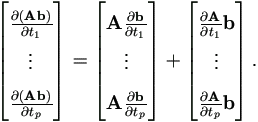 |
|
Direct Product
For vectors xn×1 and ym×1,
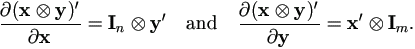 | (A.21) |
Quadratic Forms
 (x'Ax) = Ax + A'x (x'Ax) = Ax + A'x |
for asymmetric A, |
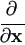 (x'Ax) = 2Ax (x'Ax) = 2Ax |
for symmetric A. |
A.2.3 Inverses
For scalar t and nonsingular matrix X, XX-1 = I gives
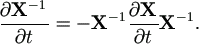 | (A.22) |
By equation (A.4), it is a special case of the following where t is a vector,
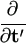 vec(X-1)
= - (X'-1 vec(X-1)
= - (X'-1 X-1) X-1) 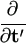 vec(X). vec(X).
|
(A.23) |
In particular by equation (A.17),
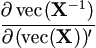 = - X'-1 = - X'-1 X-1. X-1. | (A.24) |
Assume that A and B are constant matrices and matrix X is a function of vector t,
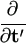 vec(AX-1B)
= - ((X-1B)' vec(AX-1B)
= - ((X-1B)'  (AX-1)) (AX-1)) 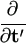 vec(X). vec(X).
|
(A.25) |
This is due to equations (A.4) and (A.23). In particular by equation (A.17),
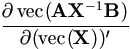 = - (X-1B)'
= - (X-1B)'  (AX-1).
(AX-1).
For vector a we have the following parallel results,
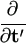 vec(X-1a) vec(X-1a) |
= - ((X-1a)'  X-1) X-1) 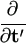 vec(X). vec(X).
| (A.26) |
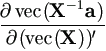 |
= - (a' X'-1)  X-1. X-1.
|
A.2.4 Determinants and Traces
Determinants
Suppose the elements of square matrix A are not functionally related and denote the cofactor of aij in |A| by |Aij|, we have
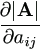 = |Aij| = |Aij| | for asymmetric A, |
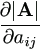 = (2 - δij) |Aij| = (2 - δij) |Aij| | for symmetric A, |
where δij is the Kronecker delta, δij = 0 for i ≠ j and δij =1 for i=j.
Suppose elements of matrix A are functions of scalar t, then
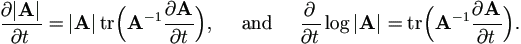
For vector t, since tr(AB) = (vec A')' vec B, it is easy to verify
| and | 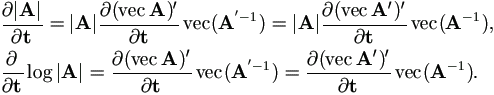 |
(A.27) |
Traces
Suppose matrix A and matrix X are not functionally related. Then
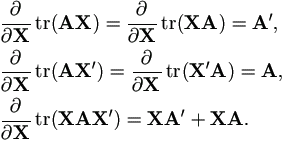
A.2.5 The Second Derivative
Suppose f (x) is a differentiable scalar function of vector xq×1. The second derivative is a symmetric matrix
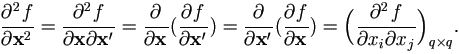 | (A.28) |
Lemma A.5
Assume vector  is a differentiable function of vector θp×1, and l(
is a differentiable function of vector θp×1, and l( ) is a scalar differentiable function of
) is a scalar differentiable function of  , then
, then
 | (A.29) |
Proof.
This is due to the chain rule (A.15) and the
Lemma A.4 with setting
θ = t, A= 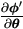 and
b=
and
b=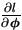 . Finally
equation (A.4) is applied to vec(
. Finally
equation (A.4) is applied to vec(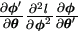 ).
).