Non Recursive BB Tree
implementation by Satin Hinge

(aka Binary B-Tree or Binary 2-3 Tree)

Deletion Algorithm

1. Tag v to be removed by setting it to the level of its child.

2. If it has no children then set it to sentinel level.

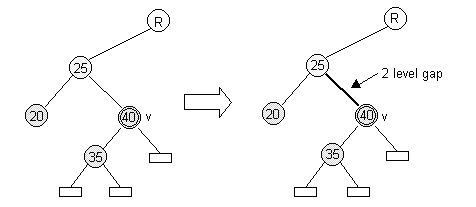	(mirror case)
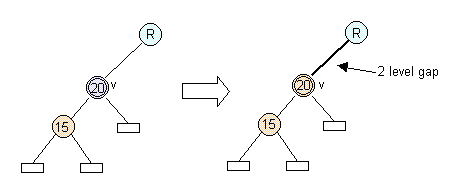	(mirror case)

3. While a two level gap exists, perform one of the following actions...

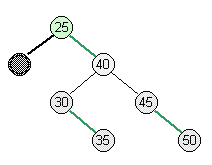
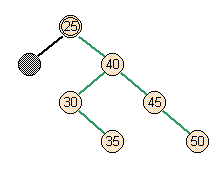
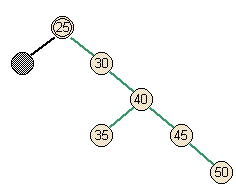
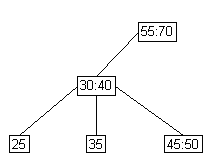
Case 1: worst case

Full parent, full siblings

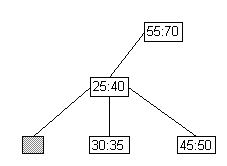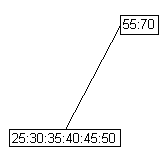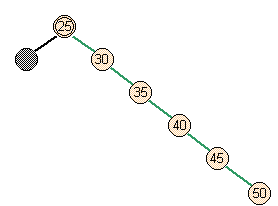lower parent and its psuedonode	skew right	skew right right	split

 

split right

 

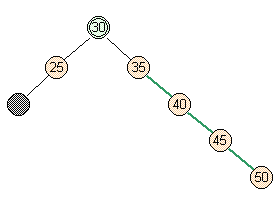
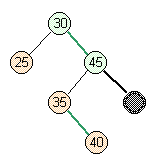
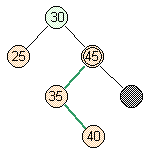
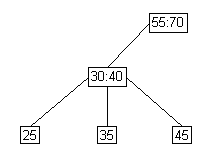
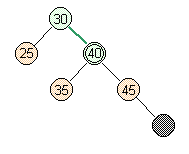
Case 2: moderate case

Full parent, full siblings.
But on the other side of the psuedonode.

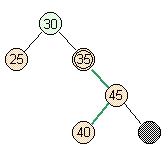lower parent	skew	skew right

 

split

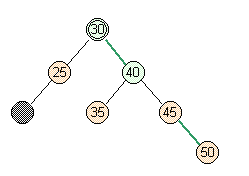
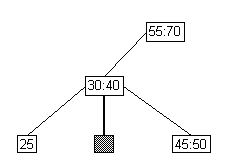
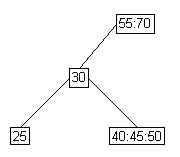
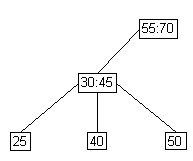
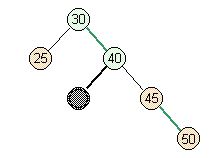
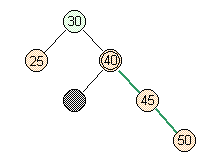
Case 3: Easiest Case

Full parent, full siblings.

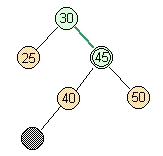lower parent	split

Insertion Algorithm

1. Insert new node at level 1

2. While a violation exists, perform one of the following actions

Violations

 

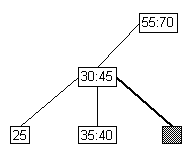
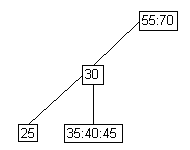
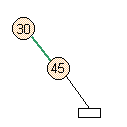
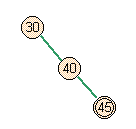
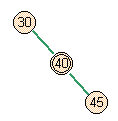
Case 1: Right side of full parent.

No skew occurs, but there's a higher split violation.

	add node	test for skew

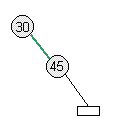
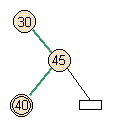
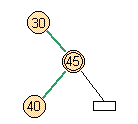
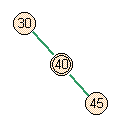
Case 2: Middle of full parent

Skew does occur, but there's a higher split violation.

	add node	skew	will split on next pass

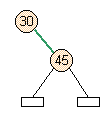
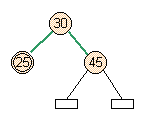
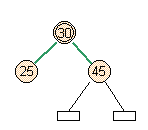
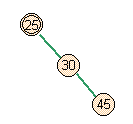
Case 3: Left side of full parent

Skew occurs, and there's an immediate split voilation.

	add node	skew	split

You can see how all the cases have been combined into a single skew and split at every node on the way up. And also why a test is made for 2 failed splits before quitting.

---

BB Tree vs Green Black Tree

(comparison)

Trial 1:

Insert ascending sequence ( 1, 2, 3 ... 29, 30, 31 )
(same as Green Black Tree)

Trial 2:

Insert descending sequence ( 31, 30, 29 ... 3, 2, 1)
(same as Green Black Tree)

Trial 3:

Insert descending sequence ( 31, 30, 29 ... 18, 17, 16 ) followed by ascending sequence ( 1, 2, 3 ... 13, 14, 15 )
(same as Green Black Tree)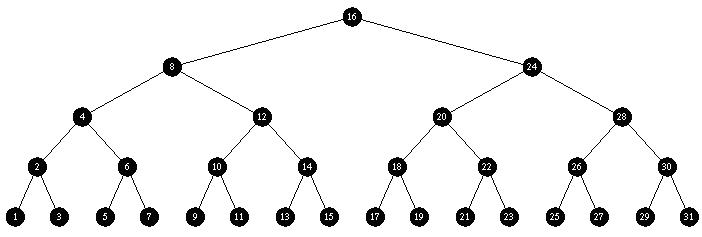

Green Black: rock solid

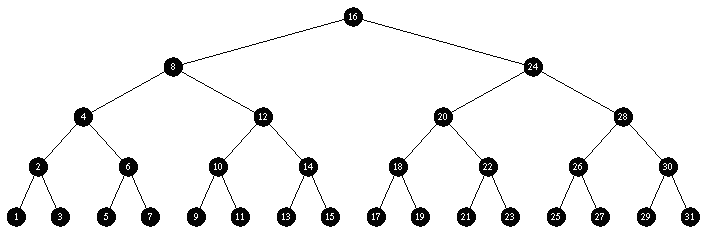
BB Tree (rendered in Green Black style): rock solid

Torture Trial:

Insert 63 random items ( in the range 1 - 545 )
repeat 100 times: { insert 480 random items into tree then delete 480 random items }

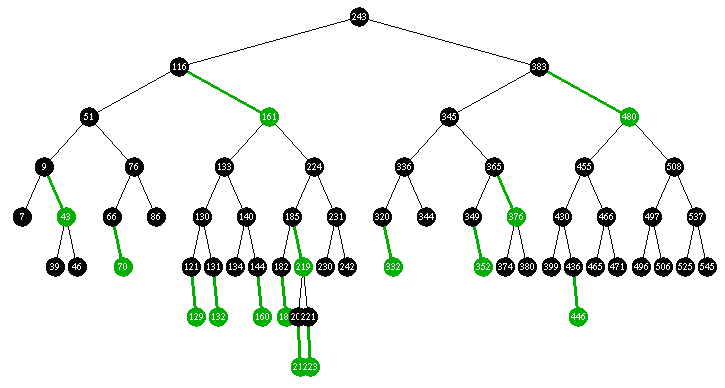
Green: handled it like a champ

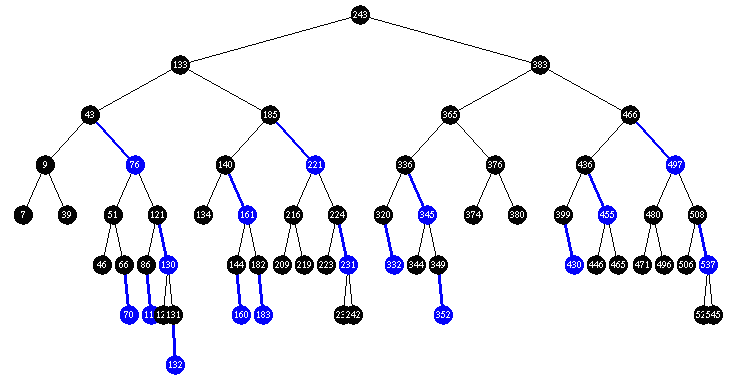
BB Tree: Hard to believe considering how simple it is

---

I'm releasing my code because of the people who are always trying to retire by the age of 30 and think that every piece of code they write is worth a million bucks. They are poor programmers and should have majored in marketing instead.

Use this code as you wish. Credit me if you like. Maybe you can even figure out how to do a top down BB-Tree.

Simplicity vs Speed
void BBTree::insertCleanup(BNodeBase *cur) { while (cur != root) { cur = cur->parent; cur = skew(cur); cur = split(cur); } }		/*void BBTree::insertCleanup(BNodeBase *cur) { bool splitlast = true; while (cur != root) { cur = cur->parent; cur = skew(cur); if ( splitTest(cur) ) { splitlast = true; cur = nakedSplit(cur); } else if (splitlast == false) { break; } else splitlast = false; } } */
void BBTree::deleteCleanup(BNodeBase *cur) { //while parent 2 levels up while ( (cur!= root) && (cur->level < (cur->parent->level - 1)) ) { cur = cur->parent; // if psuedo node extends to the right if (cur->right->level == cur->level) cur->right->level--; cur->level--; cur = skew(cur); cur->right = skew(cur->right); cur->right->right = skew(cur->right->right); cur = split(cur); cur->right = split(cur->right); } }		/* void BBTree::deleteCleanup(BNodeBase *cur) { //while parent 2 levels up while ( (cur!= root) && (cur->level < (cur->parent->level - 1)) ) { cur = cur->parent; // if psuedo node extends to the right if (cur->right->level == cur->level) { cur->level--; cur->right->level--; cur->right = skew(cur->right); cur->right->right = skew(cur->right->right); cur = split(cur); cur->right = split(cur->right); } else { cur->level--; cur = skew(cur); cur->right = skew(cur->right); cur = split(cur); } } } */
BNodeBase * BBTree::skew(BNodeBase *node) { BNodeBase *q; // to keep a level 0 node from mingling with level 0 sentinels if (node->level == 0) return node; if (node->left->level == node->level) { q = node->left; rotateRight(node); return q; } else return node; }
BNodeBase * BBTree::split(BNodeBase *node) { if ( splitTest(node) ) return nakedSplit(node); else return node; }
inline bool BBTree::splitTest(BNodeBase *node) { // to keep a level 0 node from mingling with level 0 sentinels if (node->level == 0) return false; if (node->right->right->level == node->level) return true; else return false; }
inline BNodeBase * BBTree::nakedSplit(BNodeBase *node) { BNodeBase *q; q = node->right; rotateLeft(node); q->level++; return q; }