Green Black Tree
by Satin Hinge

(Binary 2-3 Tree if done like a Red Black Tree)

 

Deletion Algorithm

  1. Remove v

  2. If v was green, color u black. Else, color u double black.

 
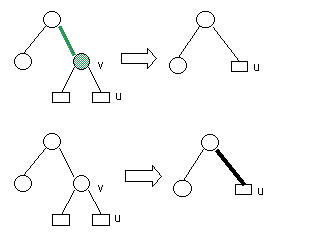(mirror case)
  1. While a double black edge exists, perform one of the following actions...
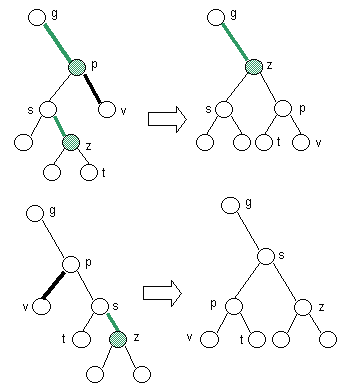
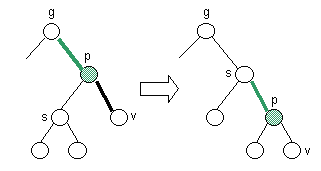
Case 1: black sibling with green right child
If sibling is black and it's right child is green, perform a restructuring.
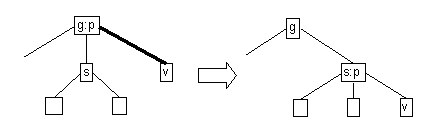
Case 2a: black right sibling with black right child
If sibling and it's right child are black, perform a recoloring.
If parent becomes double black, continue upward.
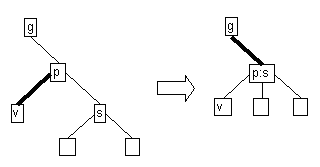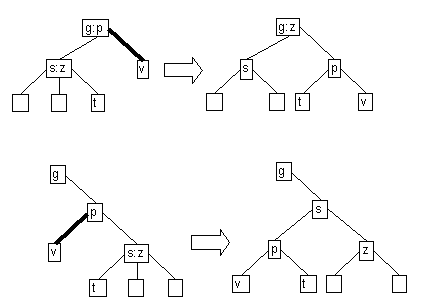
Case 2b: black left sibling with black right child
If sibling and it's right child are black, perform a restructuring.
If parent becomes double black, continue upward.
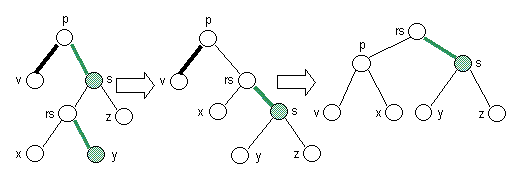
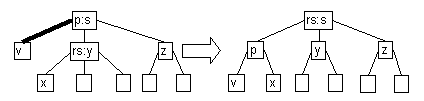
Case 3: green sibling, real sibling with green right child
If real sibling has green right child, perform a restructuring.
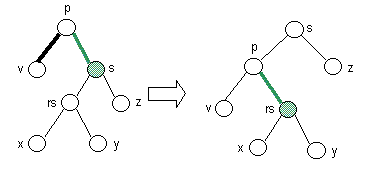
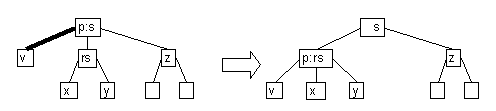
Case 4: green sibling, real sibling with black right child
If real sibling has black right child, perform a restructuring.

Relevant source code: deleteCleanup

Insertion Algorithm

  1. When inserting, insert it as green, because it must attach to an already existing pseudo node
    It can't start out as a new node because it would hang below the tree.

  1. While a green violation exists, perform one of the following actions
Green Violations
 
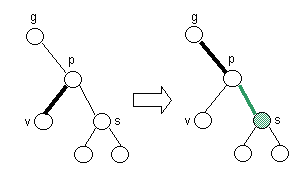
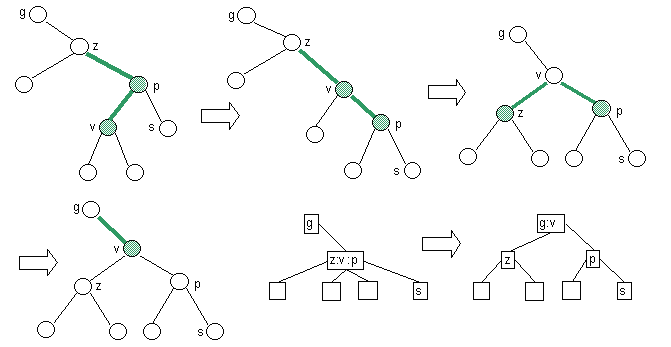
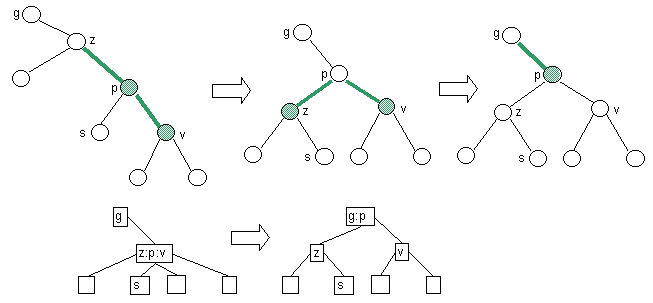
Case 1: Parent green, parent left child green.
Restructure, recolor, and continue upward.
Case 2: Parent green, parent left child black.
Restructure, recolor, and continue upward.
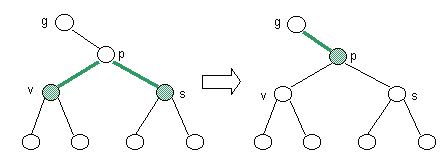
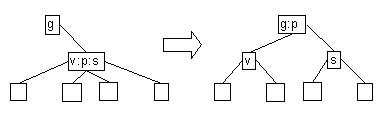
Case 3: Parent Black with green children.
Recolor, and continue upward.
Case 4: Parent black, with green left child.
Restructure.

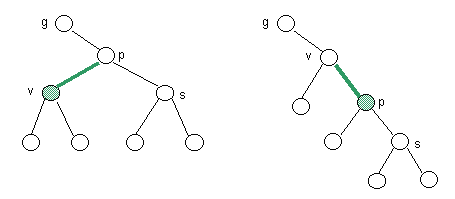Relevant source code: insertCleanup

Green Black Tree vs Red Black Tree
(comparison)

Trial 1:

Insert ascending sequence ( 1, 2, 3 ... 29, 30, 31 )

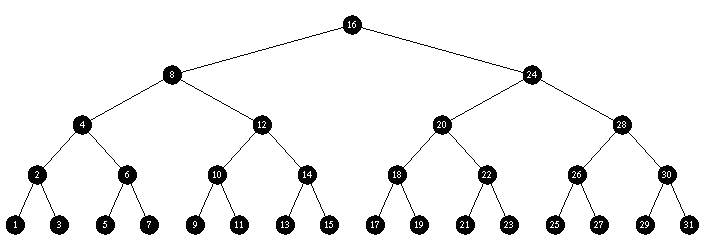
Green Black: rock solid

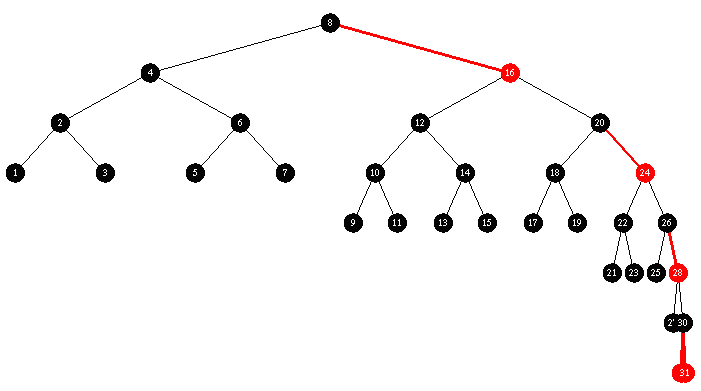
Red Black: pathetic attempt at balance

Trial 2:

Insert descending sequence ( 31, 30, 29 ... 3, 2, 1)

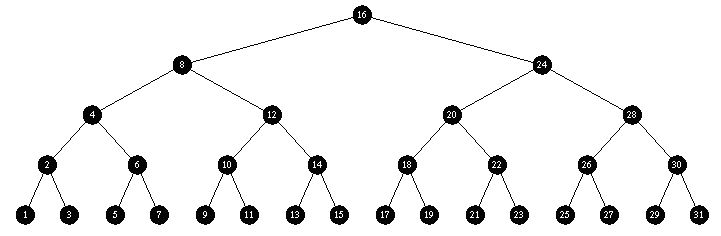
Green Black: rock solid

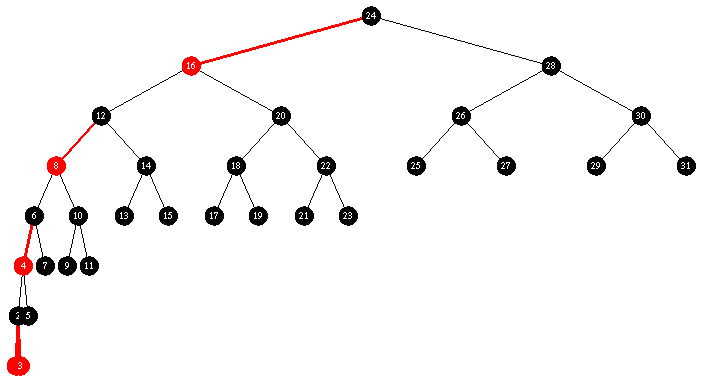
Red Black: another pathetic attempt at balance

Trial 3:

Insert descending sequence ( 31, 30, 29 ... 18, 17, 16 ) followed by ascending sequence ( 1, 2, 3 ... 13, 14, 15 )

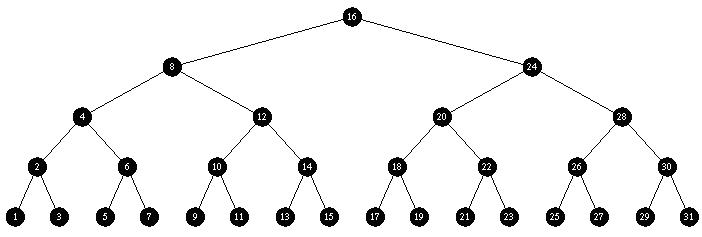
Green Black: rock solid

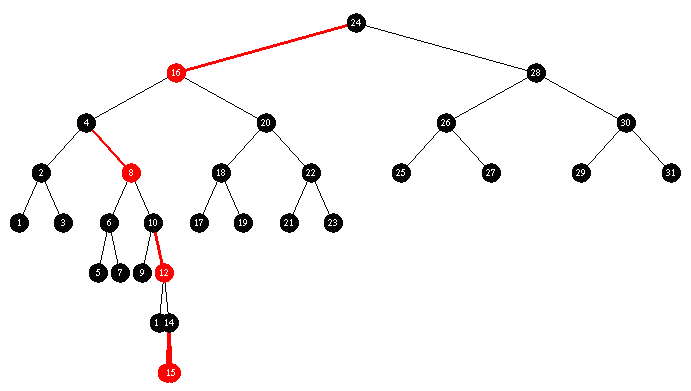
Red Black: a total breakdown, I can't believe people actually use these things

Torture Trial:

Insert 63 random items ( in the range 1 - 545 )
repeat 100 times: { insert 480 random items into tree then delete 480 random items }

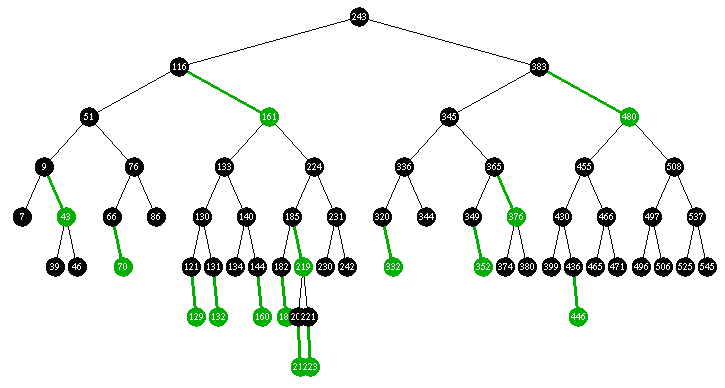
Green: handled it like a champ

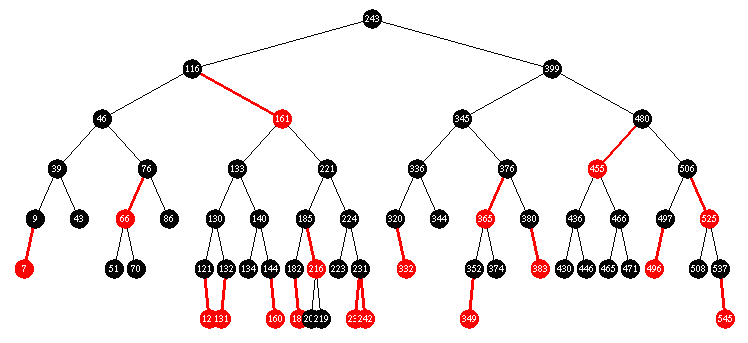
Red Black: at least it can do something

 

Summary

The Green Black tree performs just as well as the Red Black tree in similar situations. When "well behaved" data is spoon fed to it and it's nursed along like a Red Black tree, it holds it's own, but when confronted with well ordered data ( the bane of any binary tree ), it has a distinct advantage.

Now I know what you're all saying. "Aren't the Red Black tree rules complicated enough, this things a monster, I could never remember how to program it."

You're right, it is, but there's good news. There's another variant of this structure called a BB-Tree (Binary B-Tree). It uses only 2 operations: skew and split.

Taking advantage of the small node size of the structure, deleting becomes a trivial exercise; accomplished by merely merging the parent of a deleted child with all of it's children, reskewing it and resplitting. The worst case for a split is only 2 rotations, 2 rotations likewise for a skew. These can be hard wired if you use self linked sentinel nodes.

In time trials, a non recursive implementation of the Binary B-Tree has been shown to hold it's own against even a skip list and surpass it under certain circumstances.

If you have to have a tree, this is it.