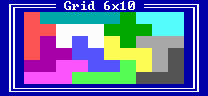
Click here to download pento.zip (22 kb).
A Polynomino is a geometric shape that you can create by joining a few number of squares of same size, side by side. According to the number of squares they are named Dominoes, Triominoes, Terominoes, Pentominoes, etc.
There are many interesting problems on Polynominoes. For example, one problem is to find out how many different Polynominoes exist of a specific type (Eg. How many Hexominoes are there?).

The 12 PentominoesThe Polynominoes make interesting objects to study for mathematicians. That's why there are numerous websites devoted on them - for example click here for a site with very good introduction to Polynominoes.
The problem that we are interested in deals with Pentominoes (i.e. Polynominoes with 5 squares). It is known that ignoring all rotations and reflections, there are 12 Pentominoes in total. According to their look, they can be coded as C, F, I, L, N, P, T, V, W, X, Y, and Z (also this is the order they are shown in the program).
Total 12 pieces each of area 5 squares each can cover up an area of 60 squares together. The puzzle is now to cover up any rectangle with area 60 (and sides measuring not less than 3 in length) using all these 12 different Pentominoes. To accomplish this you are allowed to rotate and/or reflect the pieces in any way you want.
The program gives you the ability to experiment and solve the puzzle all by yourself. However, you will never end up solving the puzzle manually, since the enormous temptation of hitting Return and letting the program solving the puzzle is absolutely irresistable. Instead, perhaps, what you can actually try is to write your own program to solve it.
Although after experimenting manually for a while the game puts the existence of solutions into question (if you do still manage to keep yourself from hitting Return), the following numbers might prove otherwise.
| Grid size | Number of solutions |
|---|---|
| 6 x 10 | 2339 |
| 5 x 12 | 1010 |
| 4 x 15 | 368 |
| 3 x 20 | 2 |