 Lesson
1: The Nature of a Sound Wave Lesson
1: The Nature of a Sound Wave
Mechanical Wave
Longitudinal Wave
Pressure Wave
Lesson 2: Sound Properties and
Their Perception
Pitch and Frequency
Intensity/Decibel Scale
The Speed of Sound
The Human Ear
Lesson 3: Behavior of Sound
Waves
Interference and Beats
The Doppler Effect and Shock
Waves
Boundary Behavior
Reflection, Refraction, and
Diffraction
Lesson 4: Resonance and
Standing Waves
Natural Frequency
Forced Vibration
Standing Wave Patterns
Fundamental Frequency and
Harmonics
Lesson 5: Musical
Instruments
Resonance
Guitar Strings
Open-End Air Columns
Closed-End Air Columns
|
Lesson 4: Resonance and
Standing Waves
Fundamental Frequency and
Harmonics
Previously in Lesson 4, it
was mentioned that when an object is forced into resonance vibrations at one of its natural frequencies, it vibrates in a
manner such that a standing wave pattern is formed within
the object. Whether it be a guitar sting, a
Chladni plate, or the air column enclosed within a
trombone, the vibrating medium vibrates in such a way
that a standing wave pattern results. Each natural
frequency which an object or instrument produces has its
own characteristic vibrational mode or standing wave
pattern. These patterns are only created within the
object or instrument at specific frequencies of
vibration; these frequencies are known as harmonic
frequencies, or merely harmonics. At any
frequency other than a harmonic frequency, the resulting
disturbance of the medium is irregular and non-repeating.
For musical instruments and other objects which vibrate
in regular and periodic fashion, the harmonic frequencies
are related to each other by simple whole number ratios.
This is part of the reason why such instruments sound musical rather than noisy. We will see in
this part of Lesson 4 why these whole number ratios exist
for a musical instrument.
First, consider a
guitar string vibrating at its natural frequency or
harmonic frequency. Because the ends of the string are
attached and fixed in place to the guitar's structure
(the bridge at one end and the frets at the other), the
ends of the string are unable to move. Subsequently,
these ends become nodes - points of no displacement. In
between these two nodes at the end of the string, there
must be at least one anti-node. The most fundamental
harmonic for a guitar string is the harmonic associated
with a standing wave having only one anti-node positioned
between the two nodes on the end of the 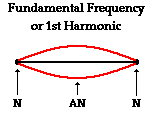 string.
This would be the harmonic with the longest wavelength
and the lowest frequency. The lowest frequency produced
by any particular instrument is known as the
fundamental
frequency. The fundamental frequency is
alternatively called the first
harmonic of the instrument. The diagram at the
right shows the first harmonic of a guitar string. If you
analyze the wave pattern in the guitar string for this
harmonic, you will notice that there is not quite one
complete wave within the pattern. A complete
wave starts at the rest position, rises to a crest,
returns to rest, drops to a trough, and finally returns
to the rest position before starting its next cycle.
(Caution: the use of
the words crest and trough to describe the pattern are
only used to help identify the length of a repeating wave
cycle. A standing wave pattern is not actually a wave,
but rather a pattern of a wave Thus, it does not consists
of crests and troughs, but rather nodes and anti-nodes.
The pattern is the result of the interference
of two waves to produce these nodes and anti-nodes.)
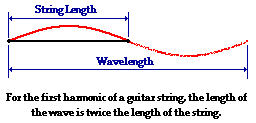
In this pattern, there is only one-half of a wave within
the length of the string. This is the case for the first
harmonic or fundamental frequency of a guitar string. The
diagram below depicts this length-wavelength relationship
for the fundamental frequency of a guitar string. string.
This would be the harmonic with the longest wavelength
and the lowest frequency. The lowest frequency produced
by any particular instrument is known as the
fundamental
frequency. The fundamental frequency is
alternatively called the first
harmonic of the instrument. The diagram at the
right shows the first harmonic of a guitar string. If you
analyze the wave pattern in the guitar string for this
harmonic, you will notice that there is not quite one
complete wave within the pattern. A complete
wave starts at the rest position, rises to a crest,
returns to rest, drops to a trough, and finally returns
to the rest position before starting its next cycle.
(Caution: the use of
the words crest and trough to describe the pattern are
only used to help identify the length of a repeating wave
cycle. A standing wave pattern is not actually a wave,
but rather a pattern of a wave Thus, it does not consists
of crests and troughs, but rather nodes and anti-nodes.
The pattern is the result of the interference
of two waves to produce these nodes and anti-nodes.)
In this pattern, there is only one-half of a wave within
the length of the string. This is the case for the first
harmonic or fundamental frequency of a guitar string. The
diagram below depicts this length-wavelength relationship
for the fundamental frequency of a guitar string.
 The
second harmonic of a guitar string is produced by adding
one more node between the ends of the guitar string. And
of course, if a node is added to the pattern, an
anti-node must be added as well in order to maintain an
alternating pattern of nodes and anti-nodes. In order to
create a regular and repeating pattern, that node must be
located exactly midway between the ends of the guitar
string. This additional node gives the second harmonic a
total of three nodes and two anti-nodes. The standing
wave pattern for the second harmonic is shown at the
right. A careful investigation of the pattern reveals
that there is exactly one full wave within the length of
the guitar string. For this reason, the length of the
string is equal to the length of the wave. The
second harmonic of a guitar string is produced by adding
one more node between the ends of the guitar string. And
of course, if a node is added to the pattern, an
anti-node must be added as well in order to maintain an
alternating pattern of nodes and anti-nodes. In order to
create a regular and repeating pattern, that node must be
located exactly midway between the ends of the guitar
string. This additional node gives the second harmonic a
total of three nodes and two anti-nodes. The standing
wave pattern for the second harmonic is shown at the
right. A careful investigation of the pattern reveals
that there is exactly one full wave within the length of
the guitar string. For this reason, the length of the
string is equal to the length of the wave.
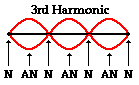 The
third harmonic of a guitar string is produced by adding
two nodes between the ends of the guitar string. And of
course, if two nodes are added to the pattern, two
anti-nodes must be added as well in order to maintain an
alternating pattern of nodes and anti-nodes. In order to
create a regular and repeating pattern for this harmonic,
the two additional nodes must be evenly spaced between
the ends of the guitar string; this places them at the
one-third mark and the two-thirds mark along the string.
These additional nodes give the third harmonic a total of
four nodes and three anti-nodes. The standing wave
pattern for the third harmonic is shown at the right. A
careful investigation of the pattern reveals that there
is more than one full wave within the length of the
guitar string. In fact, there are three-halves of a wave
within the length of the guitar string. For this reason,
the length of the string is equal to three-halves the
length of the wave. The diagram below depicts this
length-wavelength relationship for the fundamental
frequency of a guitar string. The
third harmonic of a guitar string is produced by adding
two nodes between the ends of the guitar string. And of
course, if two nodes are added to the pattern, two
anti-nodes must be added as well in order to maintain an
alternating pattern of nodes and anti-nodes. In order to
create a regular and repeating pattern for this harmonic,
the two additional nodes must be evenly spaced between
the ends of the guitar string; this places them at the
one-third mark and the two-thirds mark along the string.
These additional nodes give the third harmonic a total of
four nodes and three anti-nodes. The standing wave
pattern for the third harmonic is shown at the right. A
careful investigation of the pattern reveals that there
is more than one full wave within the length of the
guitar string. In fact, there are three-halves of a wave
within the length of the guitar string. For this reason,
the length of the string is equal to three-halves the
length of the wave. The diagram below depicts this
length-wavelength relationship for the fundamental
frequency of a guitar string.

After a discussion of the first three
harmonics, a pattern can be recognized. Each harmonic
results in an additional node and antinode, and an
additional half of a wave within the string. If the
number of waves in a string is known, then an equation
relating the wavelength of the standing wave pattern to
the length of the string can be algebraically
derived.
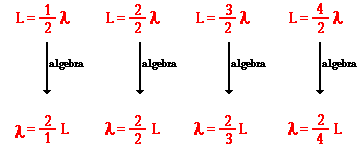
This information is
summarized in the table below.
Harm.
#
|
#
of
Waves
in
String
|
#
of
Nodes
|
#
of
Anti-
nodes
|
Length-
Wavelength
Relationship
|
|
1
|
1/2
|
2
|
1
|
Wavelength = (2/1)*L
|
|
2
|
1 or 2/2
|
3
|
2
|
Wavelength = (2/2)*L
|
|
3
|
3/2
|
4
|
3
|
Wavelength = (2/3)*L
|
|
4
|
2 or 4/2
|
5
|
4
|
Wavelength = (2/4)*L
|
|
5
|
5/2
|
6
|
5
|
Wavelength = (2/5)*L
|
The above discussion develops the
mathematical relationship between the length of a guitar
string and the wavelength of the standing wave patterns
for the various harmonics which could be established
within the string. Now these length-wavelength
relationships will be used to develop relationships for
the ratio of the wavelengths and the ratio of the
frequencies for the various harmonics played by an string
instrument (such as a guitar string).
Consider a 80-cm long guitar string
which has a fundamental frequency (1st harmonic) of 400
Hz. For the first harmonic, the wavelength of the wave
pattern would be two times the length of the string (see table above); thus, the wavelength
is 160 cm or 1.60 m. The speed of the standing wave can now be determined from the
wavelength and the frequency. The speed of the standing
wave is
speed = frequency *
wavelength
speed = 400 Hz * 1.6
m
speed = 640
m/s
This speed of 640 m/s corresponds to the speed of any
wave within the guitar string. Since the
speed of any wave is dependent upon the properties of the
medium (and not upon the properties of the wave),
every wave will have the same speed in this string
regardless of its frequency and its wavelength. So the
standing wave pattern associated with the second
harmonic, third harmonic, fourth harmonic, etc. will also
have this speed of 640 m/s. A change in frequency or
wavelength will NOT cause a change in speed.
Using the table
above, the wavelength of the second harmonic (denoted
by the symbol W2)
would be 0.8 m (the same as the length of the string).
The speed of the standing wave pattern (denoted by the
symbol v) is still 640 m/s.
Now the wave equation can be used to determine the
frequency of the second harmonic (denoted by the symbol
f2).
speed = frequency *
wavelength
frequency =
speed/wavelength
f2 = v /
W2
f2 = (640 m/s)/(0.8
m)
f2 = 800
Hz
This same process can be repeated for
the third harmonic. Using the table
above, the wavelength of the third harmonic (denoted
by the symbol W3)
would be 0.533 m (two-thirds of the length of the
string). The speed of the standing wave pattern (denoted
by the symbol v) is still
640 m/s. Now the wave equation can be used to determine
the frequency of the third harmonic (denoted by the
symbol f3).
speed = frequency *
wavelength
frequency =
speed/wavelength
f3 = v /
W3
f3 = (640 m/s)/(0.533
m)
f3 = 1200
Hz
Now if you have been following along,
you will have recognized a pattern. The frequency of the
second harmonic is two times the frequency of the first
harmonic. The frequency of the third harmonic is three
times the frequency of the first harmonic. The frequency
of the nth harmonic (where n represents the harmonic # of
any of the harmonics) is n times the frequency of the
first harmonic. In equation form, this can be written
as
fn = n *
f1
The inverse of this pattern exists for
the wavelength values of the various harmonics. The
wavelength of the second harmonic is one-half (1/2) the
wavelength of the first harmonic. The wavelength of the
third harmonic is on-third (1/3) the wavelength of the
first harmonic. And the wavelength of the nth harmonic is
one-nth (1/n) the wavelength of the first harmonic. In
equation form, this can be written as
Wn = (1/n) *
W1
These
relationships between wavelengths and frequencies of the
various harmonics for a guitar string are summarized in
the table below.
Harm.
#
|
Freq.
(Hz)
|
Wavelength
(m)
|
Speed
(m/s)
|
fn
/ f1
|
Wn
/W1
|
|
1
|
400
|
1.60
|
640
|
1
|
1/1
|
|
2
|
800
|
0.800
|
640
|
2
|
1/2
|
|
3
|
1200
|
0.533
|
640
|
3
|
1/3
|
|
4
|
1600
|
0.400
|
640
|
4
|
1/4
|
|
5
|
2000
|
0.320
|
640
|
5
|
1/5
|
|
n
|
n * 400
|
(2/n)*(0.800)
|
640
|
n
|
1/n
|
The table above
demonstrates that the individual frequencies in the set
of natural frequencies produced by a guitar string are
related to each other by whole
number ratios. For instance,
the first and second harmonics have a 2:1
frequency ratio; the second and
the third harmonics have a 3:2
frequency ratio; the third and
the fourth harmonics have a 4:3
frequency ratio; and the fifth
and the fourth harmonic have a 5:4
frequency ratio. When the
guitar is played, the string, sound box and surrounding
air vibrate at a set of frequencies to produce a wave
with a mixture of harmonics. The exact composition of
that mixture determines the
timbre
or quality of sound which is heard. If there is only a
single harmonic sounding out in the mixture (in which
case, it wouldn't be a mixture), then the sound is rather
pure-sounding. On the other hand, if there are a variety
of frequencies sounding out in the mixture, then the
timbre of the sound is rather rich in quality.
|