
Experimental Phase Tracking at COAST
In order to test the phase tracking techniques described in section 4, it was first necessary to generate some experimental photon counts. The first approach taken was to write a FORTRAN program to generate simulated data. The use of simulated data allowed the experimental parameters to be extremely well controlled so that measurement errors could be easily quantified. The program used to generate the data, fake data, is included in Appendix A of this report, along with some example output. The program is capable of simulating both photon shot noise and simple phase fluctuations.
Several 30 second data-sets were generated using the fake data routine, some with photon shot noise and simple phase modulations. The width of the carrier-wave was estimated by eye from the Fourier power spectrum. To simplify the data processing, the data-sets were split into individual sweeps and a rectangular bandwidth filter was applied to the data in each sweep independently. At low photon rates the measured phase was found to occasionally jump by one cycle in-between sweeps. This may have been related to the simplified processing technique used. Fringe tracking output from two of the tests is shown in Figures 9 and 10.

Figure 9 - Fringe tracking output using fake data with photon shot noise and phase modulation. The mean intensity of the light was 100 photons per sample and the maximum fringe visibility was 0.5.

Figure 10 - Attempted phase tracking with low light intensities was hindered by errors at the beginning and end of each sweep. The phase jumps by one cycle at several points over the two second period shown. It is thought that these errors would not have occurred if the data had been processed in one piece and not separated into individual sweeps.
|
Mean intensity (photons / sample) |
RMS error in phase measurement (radians) |
|
100 |
0.0700 |
|
10 |
0.160 |
|
1 |
Tracking lost (Figure 10) |
Table 1 - Errors in phase tracking on fake data. The peak visibility was 0.5 in each case.
The second approach taken was to generate data at the COAST telescope during daylight hours, when the telescope would not normally be in use. A point source positioned in the focal plane of a lens was used as an artificial star for the beam combining apparatus. This was put in place of one of the APDs (Figure 11). Mirrors were placed in the telescope beams after the delay lines, reflecting light back to the three remaining APDs.
†

Figure 11 - Experimental arrangement for tracking internal fringes
The delay line associated with one of the beams was modulated backwards and forwards, scanning the interference fringes past the APD detectors. As the beams passed through the delay line system twice, the fringe velocities observed were twice that which would be observed under normal telescope operation. Photon counts were digitally sampled at 5kHz for 30 second intervals on two of the remaining APDs. Large overheads in disk space, processor time and data transfer between the COAST observatory and the Cavendish Laboratories limited the amount of data which could be used in analyses.
The first data sets were recorded in stable laboratory conditions. Data was taken with a variety of different delay-line modulations. Only the data-set with the modulation of smallest amplitude was used in the fringe tracking analyses. In this data-set the detector remained well within the fringe envelope at all times.
Convection currents from a hot soldering iron were used to generate turbulence in one of the light beams, and the second data-set used in the phase-tracking experiments was taken under these conditions. The delay-line modulations used were identical to those for the first data-set. Under normal operation at COAST the input beams are spatially compressed, causing angular deflections in the incoming beams to be magnified by a factor of sixteen. In order to accurately simulate atmospheric fluctuations, the turbulence in the laboratory would thus need to be on a scale sixteen times smaller than that observed in the atmosphere. Clearly the turbulence created by a soldering iron will not be exactly identical to that generated on a larger scale in the atmosphere. It was hoped that the data would still prove useful for testing the phase-tracking software.
The delay lines at COAST are not capable of producing an exact sawtooth wave modulation, and the systematic errors in delay line position have been tabulated for modulations with several specific amplitudes. Figure 12 shows some example delay line position data and Figure 13 shows the deviation from an ideal sawtooth wave, averaged over twenty sweeps. Unfortunately this data was not available for the slow speed modulations necessary for tracking internal fringes. It was therefore assumed for the purposes of the fringe tracking experiments, that the delay line motion followed an ideal sawtooth wave. The phase errors resulting from this assumption were relatively large at the beginning and end of each sweep. In initial analyses there was a tendency for the phase to jump by one or more cycles between sweeps.

Figure 12 - Trolley position against time for a typical 200ms interval. Sawtooth modulation of amplitude 10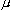 m applied.
m applied.

Figure 13 - Deviations from ideal sawtooth wave averaged over twenty sweeps. The measured errors in each individual sweep were typically within 5% of the mean values shown in this Figure.
In order to allow accurate tracking from one sweep to the next I decided to numerically filter the intput data so as to remove high frequency phase fluctuations. This was done by replacing
arg(Ií(t +  t)Ií*(t)) the phase change over the period t, t +
t)Ií*(t)) the phase change over the period t, t +  t
t
in Equation 4 with
 the weighted average of the same result over the period
the weighted average of the same result over the period
t - n t, t + (n + 1)
t, t + (n + 1)  t
t
where the weighting is based upon the strength of the carrier signal. This numerical filter is designed to reject sudden jumps in the phase of the input while
accurately tracking the gradual fluctuations produced by atmospheric effects. A small amount of phase drifting can occur if it is applied to large data-sets. A value of n
was chosen such that n t was roughly 10ms, hence filtering out Fourier components with frequency greater than about 50Hz.
t was roughly 10ms, hence filtering out Fourier components with frequency greater than about 50Hz.
Figure 14 shows two phase tracking traces each 0.5 seconds long generated using this technique. There are small bumps in the traces at 0.1 second intervals corresponding to the time-points where the delay line reversed direction. The Fourier power spectrum of 30 seconds of output from each of the analyses is shown in Figure 15. The spikes at 5Hz intervals on the lower trace are thought to be the result of phase errors at the beginning and end of each sweep.

Figure 14 - Sample experimental data. The top trace shows the results of fringe tracking with a soldering iron place beneath the beam. The bottom trace was taken with no applied turbulence.
The Kolmogorov model of atmospheric turbulence2 predicts that the power spectrum of phase fluctuations should obey the following relation:
![]() where P(
where P(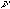 ) is the power in the
) is the power in the 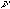 th Fourier component. The data in Figure 15 are broadly in agreement with this.
th Fourier component. The data in Figure 15 are broadly in agreement with this.

Figure 15 - Fourier power spectrum of phase fluctuations with internal fringes. The top trace shows the results of fringe tracking when a hot soldering iron was placed beneath the beam. The bottom trace was produced from data taken with no applied turbulence. The spikes at 5Hz intervals in the bottom trace are though to be artifacts of the experimental arrangement.
Return to Bob's Interferometry Page.
Return to Bob's Home Page.