Tracking the position of the Fringe Envelope
If the two beams on one baseline are undispersed, all wavelengths of light will interfere constructively at one point within the sweep – the point where the optical path lengths from light source to the detector are equal (labelled point C in Figure 16). If the light intensity measurements within a sweep are Fourier transformed, it will be found that all the Fourier components associated with the carrier-wave also interfere constructively at this point.
Figure 16 – C is the point where all Fourier components interfere constructively
This allows the position of the centre of the fringe envelope to be measured easily and relatively accurately even with extremely faint light sources. The point where the most constructive interference occurs between Fourier components of the carrier can be calculated from the phase of the complex number C, defined as:
Equation 5
where G(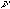
) is the Fourier component of the light intensity at frequency
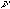. The summation should be performed over all Fourier components that are associated with the carrier wave. The position of the centre of the fringe envelope is linearly related to 
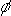, where
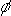is the phase of C, i.e.
C = Aexp(i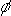
) 
Equation 6
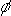ranges from zero when the centre of the envelope is at the start of the sweep to 2
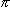when it is at the end. As the fringes move by only a small fraction of the length of the sweep every second, the summation in Equation 5 can be performed over Fourier components of the carrier taken from a number of different sweeps. If one of the incoming beams is dispersed more than the other, or if the position of the fringes is varying,
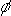will represent a weighted average of the positions of the fringe envelope centre at each wavelength and at each time. The weighting is based upon the amplitudes of the relevant Fourier components. Several example measurements of this type are shown in Section 7.
This type of measurement might be extremely helpful for finding the location of the interference fringes on a baseline, and for monitoring the drift of the fringe envelope which often takes place during astronomical observations. As the technique uses only the Fourier components of the carrier it should also work successfully during closure phase measurements, when there are three or more carrier-waves present.
Return to Bob's Interferometry Page.
Return to Bob's Home Page.