The first two techniques discussed here are designed to treat all wavelengths of light equally, rather than biasing the measurements towards light of a particular spectral composition. This requires that all Fourier components of the carrier-wave and all parts of the fringe envelope are treated in the same way.

In order that a phase measurement is based upon all the Fourier components from the carrier, I’(t) must be numerically filtered using a system which responds equally to each of the Fourier components. The simplest example is a rectangular filter having the same width as the carrier signal. The measured phase should be a weighted average of the phases of the different Fourier components in the carrier-wave signal, with weighting based upon the relative amplitudes of the Fourier components. In this way the phase measurement will not be biased towards any wavelength of light.

To ensure that a phase measurement is equally weighted by the signal from different parts of the fringe envelope, it is necessary firstly to ensure that all of the fringe envelope is scanned past the detector, and secondly to ensure that a weighted average of the phase over a whole sweep is used. The weighting should be based upon the amplitude of the carrier-wave signal.

The simplest suitable measurement of the fringe phase is a weighted average of the phase of I’(t) over each sweep, where the weighting is based upon the amplitude of I’(t). At very low light intensity this technique is likely to be limited by phase-wrapping errors.

If the incoming beams are not dispersed, all the Fourier components in the carrier-wave will interfere constructively at one point. All the Fourier components of the carrier signal will then be related in the following way:

where G(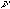 ) is the Fourier component of the carrier signal at frequency 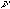and 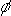indicates the position within the sweep where all the Fourier components interfere constructively (defined by Equations 5 and 6 in Section 6). Each individual Fourier component can thus provide an independent measurement of the fringe phase. Each component in the carrier wave is generated by light of a different spectral composition. If all of these contributions are averaged with weighting based upon the amplitude of the Fourier component, an estimation of the fringe phase will be given which is not biased towards any particular wavelength of light. The second technique attempts to do this, estimating the fringe complex amplitude as follows:

Equation 7

where G(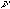 ) and are as defined for Equations 5 and 6. It should be noted that under low light conditions the value of 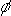can be averaged over several seconds, as described in Section 6.

If different degrees of optical dispersion are applied to the two incoming beams, the phase of I_F will represent a weighted average of the contributions from different Fourier components in the carrier-wave. The phase of each of these Fourier components is determined by light of a different spectral composition, but as the weighting is based upon the light intensity, the overall spectral response will be the same on each baseline.

With the current system of delay line motions (Figures 19 and 20), the requirement that the whole fringe envelope is scanned past the detector on even the slowest baseline would entail that the fringes on the faster moving baselines were out of range of the detectors for much of the time. An alternative scheme for the delay-line motions which allows the detector to remain within the fast-moving fringe envelopes for a larger proportion of the time is shown in Figures 27 and 28. In the new scheme each of the delay lines moves at two different speeds at different times in a four-stage cycle (Figure 27). An identical cycle is used on each of the three baselines, although the modulations run of a cycle out of phase with each other. It is not possible for dispersion to produce systematic effects on closure phase measurements in this case because the same modulations are applied to each beam. These delay line motions thus in themselves represent a technique for removing the systematic effect of optical dispersion from closure phase measurements.

In order for successful fringe measurements to be made, the fringes on all three baselines must move at different speeds, so that the carrier-waves for each of the baseline contribute different Fourier components to the measured intensity. To keep the detector within the fringe envelope for a greater proportion of the time, the fringes on the two fastest baselines (the baselines on which the fringes move fastest) reverse direction halfway through the sweep. The two delay lines associated with the fringe motion on the slower baseline are unaffected. The direction of motion of the delay lines is changed by applying a sharp impulse to the mirrors through an attached electromagnetic coil. The change in the velocity on the two faster baselines will not be instantaneous. For a short period of time the fringes on these baselines will be moving at the same speed as the fringes on the slower baseline. The interference between the carrier-waves will cause a few samples from the centre of the sweep to be unusable for phase measurements on the slower moving baseline. However, the baselines take it in turns to have the slow fringe rate, so no systematic errors can be generated by the lost samples.

Figure 28 shows the fringe motions produced. If the width of the fringe envelopes on each baseline fill two units on the left-hand (arbitrary) scale in this figure, the detector will remain within the fringe envelopes on all of the baselines for a large proportion of the time. This may increase the signal to noise in complex closure amplitude measurements by a factor of two relative to the old system. Even if the detector passes through the fringe envelope twice during the sweep, phase measurements on each baseline should be averaged over each whole sweep.

Processing data taken using this scheme would probably be a little more complex than for the current system. The approximation that delay lines move at constant velocity between impulses might not be valid as the delay lines have less time to settle down to the correct velocity. This does not pose a serious problem for the data processing as long as the positions of the delay lines can be accurately monitored / estimated at all times.

One of the potential problems with this scheme stems from the fact that the phase measurements on different baselines take place at slightly different times. If the phase errors due to the atmosphere are changing very rapidly, additional random errors will be introduced into the closure phase measurements.

Return to Bob's Interferometry Page.

Return to Bob's Home Page.