[Homepage] [Bricks Game Page] [Maths Page] [Music Page] [Sign my GuestBook]
1. Let O be the circumcenter of DABC. Suppose AB > AC > BC. Let D be a point on the minor arc BC. Let E and F be points on AD such that AB ^ OE and AC ^ OF. Let P be the intersection of BE and CF. If PB = PC+PO, then prove that Ð BAC = 30°.
Ans:
2. Let a1 = 1, an+1 = an/n + n/an for n = 1, 2, 3, ... Find the greatest integer less than or equal to a2000. Be sure to prove your claim.
Ans:
a1 = 1
a2 = 1/1 + 1/1 = 2
a3 = 2/2 + 2/2 = 2
a4 = 2/3 + 3/2 = 13/6
Notice that sqrt(4) < a4 < sqrt(5).
i.e. an > sqrt(n) for n = 4 -----------(1)
i.e. an < sqrt(n+1) for n = 4 -------(2)
Prove an+1 > sqrt(n+1) for all integer n > 3, given (1) is true (by Mathematical Induction):
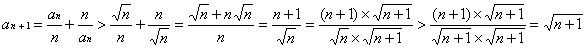
Therefore an+1 > sqrt(n+1) is true for all integer n > 3.
Therefore a2000 > sqrt(2000).
Prove an+1 < sqrt(n+2) is true for all integer n > 3, given (2) is true (by Mathematical Induction):
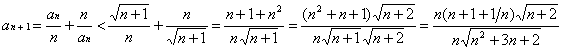
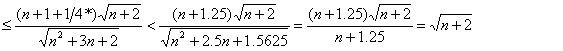
* 1/n £ 1/4 for all integer n > 3.
Therefore an+1 < sqrt(n+2) is true for all integer n > 3.
Therefore a2000 < sqrt(2001).
Notice both sqrt(2000) and sqrt(2001) lie between 44 and 45.
Therefore the greatest integer less than or equal to a2000 must be 44.
3. Find all prime numbers p and q such that [(7p - 2p)(7q - 2q)] ÷ (pq) is an integer.
Ans: (provided by Marco Roger Graf and Simon Mok)
This is not a prove, just some bits and pieces of ideas.
a) 7p is always odd 2p is always even. This means 7p - 2p must be odd for all p (i.e., not divisible by 2). Same to q. Hence p and q cannot be 2.
b) p=5 and q=5 is an answer (by observation)
c) p and q cannot be 7, since 7x - 2x is not divisible by 7 for all x.
d) p=5 and q = 11 is another answer (by observation)
e) p and q cannot be 3. Prove: (sorry, don't know how to prove!)
4. A lattice point on the coordinate plane is a point with integer coordinates. Find all positive inter n ³ 3 such that there exists an n-sided polygon having lattice points as vertices and all sides have equal length.
Ans:
The following quadrilateral can be made with all sides having the same length, with bottum-right point at (0, 0), top-right point at (8,4). The other 2 points are (5, 0) and (3, 4). The length of all 4 sides are 5 units, and all points are lattice points.
__ / / ¯¯
The quadrilateral could be extended to have 6 sides, like this:
__ \ \ / / ¯¯
The added points would have coordinates of (0, 8) and (5, 8). It is a 6-sided polygon, and all points are lattice points.
The pattern can be extended indefinitely, for 8-sided polygon, 10-sided polygon ... so n could be any even number > 3.
But how to do the odd number ones??????????
5. There are 10 persons at a meeting. Among them, each person is familiar with at least 5 other persons. Show that 4 persons can be selected and seated at a round table so that every one at the table is familiar with his/her neighbours.
Ans:
Let the 10 persons be A, B, C, ..., J. They are named in random and there is no particular order.
Let the selected 4 persons be A, B, C and D. Let A and C sit opposite to each other, so do B and D.
For person A, he would choose to sit next to the 2 of the 5 (or more) person that he is familiar with. So he must be familiar with B and D. He may or may not be familiar with C.
Person A must also make sure that B and D are not familiar with each other, if one of them is familiar with only 5 persons ¹.
Now, prove there is a person C who is familiar with both B and D (by proving B is familiar with C and D is familiar with C)..
To be conservative assume B and D are both familiar with 5 persons only (if they know more it is easier to find person C). From above, B knows A and not D (from ¹). Assume the other 4 that he knows are C, E, F, G. From above, D knows A but not B (from ¹). In the worse case, 3 of the other 4 that he knows are H, I, J (which B doesn't know), but the forth person that D knows must also be familiar with B (we cater for all 10 persons already, namely, A to J). Say the person is C (can be E, F or G; the name is different but the idea is the same)
So, now, A is familiar with B and D. A could be either familiar with or not familiar with C. B and D must not be familiar with each other if one of them is familiar with only 5 persons. B is familiar with A and C (proven), C is familiar with B and D (proven), and D is familiar with C and A (proven). Therefore 4 persons can be selected and seated at a round table so that every one at the table is familiar with his/her neighbours.
6. A squash club has 20 members. 14 matches have been played among the members, and it is discovered that each member has played at least once. Show that among the 14 matches we can pick out 6 such that the 12 players involved in these 6 matches are all different persons.
Ans: (by Kurt Neuenschwander)
The numbers are fixed (not variable or indefinit), therefore it is a finite problem and can be solved step by step with logic (as in Bricks). Take the WORST CASE and proove, that in the WORST CASE it is still possible find 6 matches with 12 different players. The formulation of the WORST CASE is the tricky part.
GIVEN: x selected matches and (x*2) selected players "all different" (x=1,2,3,4,5,6, ... )
WORST CASE: it is not possible to select another match with 2 players, from the
remaining (14 - x) matches and remaining (20 - x*2) players.
THAT MEANS: It needs (20 - x*2) matches, for each unselected player to play AT
LEAST ONCE,
but not 2 of them against each other. (WORST CASE).
THAT MEANS there are 14-x remaining matches for these 20 - x*2 needed matches.
14-x >= 20 - 2x; x >= 6
THAT MEANS it is not possible to select another match with 2 players, from
the remaining list if x is >= 6.
THAT MEANS when x =5 it is still possible to select another match with 2 new players,
which gives you 6 matches with 12 different players.
Here is a number example, for better understanding: It's obviously always existing 1 match with 2 different players.
Let's select match A with Players Z,Y.
--> remaining 13 matches (14 -1) and 18 players (20-2*1) .
I will proove, that following statement is FALSE:
"It is NOT possible to find a 2nd match B, with 2 new players W,X."
If the statement would be true, it would mean, that: from the 18 remaining players, each played AT LEAST ONCE, but none of them in the same match (each played only against the 2 Players Y,Z). there are AT LEAST 18 matches necessary for this. But there are only 13 matches remaining, for these 18 players. Therefore the statement is wrong.
Therefore it's prooven, that when 1 match is selected, it's
possible to find a 2nd match with 2 new players.
The same proove shows that it's possible to find a 3rd match
from the remaining 12 (14-2) matches and (20-2*2) 16 players.
The same proove shows that it's possible to find a 4th match
from the remaining 11 (14-3) matches and (20-2*3) 14 players.
The same proove shows that it's possible to find a 5th match
from the remaining 10 (14-4) matches and (20-2*4) 12 players.
The same proove shows that it's possible to find a 6th match
from the remaining 9 (14-5) matches and (20-2*5) 10 players.
The prove does not work anymore, with remaining 8 matches and 8 players. Each one could have played in a different match against any of the already selected 12 players. It might be, or it might not be. Who knows?
If "selected players" played more than once. There's a better chance to find MORE THAN 6 matches, but prooven is only that it's AT LEAST 6 matches with 12 different players. if "already selected players" played 2 or more matches, it even improves the chance, that 2 "remaining players" must have played against each other.
Which helps you
find "new" players in the "remaining matches".
This is because of the 2 conditions:
- Each player played AT LEAST ONCE
- ONLY 14 matches were played
7. In a room there are 100 men. Each man was a friend of at least 67 other men in the room. All of the 100 persons would only play bridge with three of their friends. Show that every man in the room can find 3 others such that the group of 4 can sit down and play bridge.
Ans: