Question:
Problem 11.13: 1Test is appropriate for Multiple Testing:

a. Tukey - Kramer Procedure - for unequal sample sizes

Given in Problem 11.13:

MSE = 1.26
C = 3
N = 18
N - C = 15
alpha = .05
q.05,3,15 = 3.67

HIGH LEVEL MIDLEVEL LOW LEVEL     7 8 5     7 9 6     8 8 5     7 10 7     9 9 4     10 8       8   TOTAL(rows): 38 62 35 135 n 5 7 6 N =18 7.6 8.86 5.83 7.5

Solutions:

We use the Tukey - Kramer Procedure for unequal sample sizes.

There will be 3 possible pair wise combinations:
C(C-1) / 2 or 3(3 - 1) / 2

Tukey - Kramer Formula:

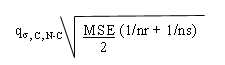
For High and Mid Level Comparison:

3.67 x sqrt of [1.26/2 (1/5 + 1/7)]

critical difference of 1.71

The actual difference between high and mid level managers is 7.6 - 8.86 = 1.26. 1.26 is less than the
critical difference of 1.71 therefore there is no significant difference between the means of high and mid level
managers.

-------------------------------------------------------------------------------------------------------------------------------------------------------

For High and Low Level Comparison:

3.67 x sqrt of [1.26/2 (1/5 + 1/6)]

critical difference of 1.76

The actual difference between high and low level managers is 7.6 - 5.83 = 1.77. 1.77 is greater than the
critical difference of 1.76 therefore there is a significant difference between the means of high and low level managers.

-------------------------------------------------------------------------------------------------------------------------------------------------------

For Mid and Low Level Comparison:

3.67 x sqrt of [1.26/2 (1/7 + 1/6)]

critical difference of 1.62

The actual difference between mid and low level managers is 8.86 - 5.83 = 3.03. 3.03 is greater than the
critical difference of 1.62 therefore there is a significant difference between the means of mid and low level managers.

Summary Table:

There is a significant difference in evaluations between high and low managers and mid and low managers only.

Back to: Finals Main Page