SEÇÃO I

» 1ª Unidade: História e Conceitos Básicos

• A Estrutura do Jogo: Conceitos e princípios

A palavra "jogo", que dá nome à teoria, foi alvo de diversos malentendidos desnecessários. Muitos consideravam a Teoria dos Jogos como algo frívolo, pouco sério, ou simplesmente não-científico, dada sua origem em estudos de jogos de salão, como pôquer, xadrez ou "pedra, papel e tesoura". Por ter sido gerada num ambiente predominante de homens e antes dos movimentos sociais exigirem do mundo acadêmico a colocação de expressões "politicamente corretas", a teoria está povoada por conceitos cujos termos fazem referências à "batalha dos sexos", "conversa barata" (cheap talk), "blefe" e "pato" (sucker), entre outros jargões menos chocantes. Tecnicamente, no entanto, essa má impressão desfaz-se quando se percebe que a aparente simplificação das relações entre indivíduos fornecida pela formalização matemática da teoria permite analisar com uma precisão até então desconhecida nas ciências sociais o comportamento dos agentes "racionais", humanos ou não.

Para a Teoria dos Jogos, um jogo é definido por um conjunto de regras que estabelece seus cinco elementos constitutivos:

1. o número de participantes;
2. as ações ou estratégias possíveis;
3. os resultados de cada jogador;
4. a função que permite a cada parte combinar suas estratégias e
5. a relação de preferências de cada um diante dos resultados.

Além disso, as regras delimitam o grau de informação permitido aos agentes. Os jogos são representações simplificadas de situações onde pelo menos uma pessoa age no sentido de maximizar a utilidade de suas ações levando em conta as reações de outros agentes. Trata-se, portanto, da descrição formal de uma situação interativa estratégica em que as partes devem resolver qual a melhor decisão a ser tomada, segundo o ponto de vista de um agente capaz de computar quais meios serão necessários para obtenção do fim esperado. Por conseguinte, um jogador possui como requisito mínimo uma racionalidade instrumental ou estratégica.

Jogos com apenas uma pessoa são considerados jogos contra a natureza (ou Sorte) - único agente considerado não-racional, mas que pode gerar indeterminação aos resultados, que passam a ser influenciados pela lei da probabilidade. A rigor, não há empecilhos formais para o estudo de jogos com um número infinito de participantes, embora seja mais frequente a pesquisa dos casos que envolvem duas partes, cuja visualização pode ser feita facilmente na forma dita normal, ou estratégica, e na forma extensiva. Na sua representação normal, ou estratégica, os jogos são apresentados em matrizes nas quais as estratégias de cada jogador são listadas respectivamente nas linhas e colunas. Em cada célula da tabela aparecem os ganhos que cada uma das partes obterá caso realize as ações às quais ambas estão vinculadas. Os ganhos do jogador da linha são grafados na primeira posição, à esquerda do par ordenado, e os do jogador da coluna vêm após a vírgula que os separa, à direita. A figura 1 expôe a representação geral da forma estratégica:

Figura 1 - Matriz Geral de Estratégias Puras		Coluna
		1	2	....	y2	....	yn
Linha	1	f(1, 1)	f(1, 2)	....	f(1, y2)	....	f(1, yn)
	2	f(2, 1)	f(2, 2)	....	f(2, y2)	....	f(2, yn)
	: :	: :	: :		: :		: :
	x1	f(x1, 1)	f(x1, 2)	....	f(x1, y2)	....	f(x1, yn)
	: :	: :	: :		: :		: :
	xm	f(xm, 1)	f(xm, 2)	....	f(xm, y2)	....	f(xm, yn)

As matrizes servem para mostrar de forma compacta as respostas que podem ser esperadas em função das ações escolhidas simultaneamente. Aqui a ordem em que os jogadores atuam é irrelevante ao resultado. Também são desconsideradas a quantidade de vezes que os jogos se repetem, sendo a matriz o resumo de todos jogos possíveis em suas rodadas infinitas, ou indeterminadas. A matriz concentra as informações disponíveis a cada jogador por igual. Por outro lado, dificulta a inclusão de um número muito grande de jogadores. Acima de dois jogadores, a representação deixa de ser bidimensional e passa a ser tridimensional, com três participantes, ou multidimensional, para mais de quatro jogadores.

Jogos em que os detalhes omitidos pela forma estratégica são relevantes ficam melhor representados na descrição completa fornecida pela forma extensiva, desenhada no modelo estrutural de "árvores". No esquema de árvores, a ordem deliberativa de cada jogador é observada, bem como o conjunto de informações de cada um. Os pontos apresentados - ou "nós" - são as decisões disponíveis e os traços - ou "ramos" - as alternativas de movimento e as ações que levam de um nó a outro, desde o ponto inicial - ou "raiz" - até o resultado final em cada terminal. O caminho traçado, da raiz à "folha", delineia todas as estratégias que podem ser realizadas. Motivo pelo qual as árvores só devem ser empregadas em jogos finitos. A forma extensiva permite uma análise direta da situação, já que apresenta toda estrutura das jogadas e das informações disponíveis de uma vez. Observando os nós e ramos da árvore, podem ser percebidos o número de jogadores, suas opções nos pontos de decisão, as posições intermediárias - ou movimentos - até os nós terminais e a quantidade de jogadas a cada passo executado (1). O conjunto de informação de cada jogador é limitado em cada rodada por uma linha que circunda os nós de decisão. Quando o jogador tem certeza em qual nó se encontra, este conjunto de informação é unitário. Cada nó e conjunto de informação é rotulado com o número ou letra de cada jogador, enquanto os ramos são rotulados com as alternativas de ação que partem de cada nó. As árvores são apropriadas para os jogos sequenciais, onde os agentes se movimentam numa ordem predeterminada (figura 2).

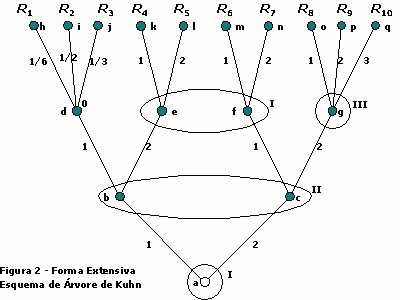
No exemplo da figura 2, vê-se a raiz, representada pelo ponto aberto "a", corresponder ao conjunto unitário de informação inicial do jogador I, que tem duas linhas de ação a sua escolha, 1 ou 2. O jogador II deverá na sequência escolher também entre suas opções 1 ou 2. Contudo, dependendo do nó em que se localize, "b" ou "c", poderá levar com que a natureza, jogador 0, venha executar o próximo movimento, caso sua alternativa 1 seja adotada a partir do nó "b". Assim, haveria a probabilidade dos resultados de "R₁" a "R₃", ocorrerem nas proporções que nomeiam seus respectivos ramos. De outro modo, se II selecionasse a estratégia 2, desde o ponto de decisão "c", o jogador III entraria em cena para optar por uma de suas três ações que conduzem aos ganhos de "R₈" a "R₁₀". Do contrário, as demais alternativas retornam a I a chance de escolher entre "R₄" e "R₅", decidindo a partir de "e", ou "R₆" e "R₇", saindo de "f". Todos os dez resultados possíveis deste exemplo distribuiriam, ao final, os pagamentos devidos aos três jogadores envolvidos (I, II, III), já que a natureza (0), embora possa atuar como um agente irracional gerador de incerteza, não obtém nenhum ganho das ações empreitadas.

A definição mais geral da forma extensiva para jogos com n-pessoas foi estabelecida por Harold W. Kuhn, em 1953, no artigo "Extensive Games and the Problem of Information" ("Jogos Extensivos e o Problema da Informação"), ampliando a versão apresentada por John von Neumann, em 1928. A chamada árvore de Kuhn atende a sete condições:

1. Um conjunto de n jogadores;
2. Estrutura de árvore enraizada, chamada árvore do jogo;
3. Partição do conjunto de nós em diversos subconjuntos, entre os jogadores;
4. Distribuição de probabilidade rotulando cada ramo brotado de um nó do subconjunto da natureza, jogador 0;
5. A formação de conjunto de informações para cada subconjunto de nós de um jogador deve respeitar (a) o mesmo número de ramos correspondentes, saindo de cada nó diferente, e (b) cada caminho, partindo da raiz à folha, só pode cruzar um conjunto de informação uma única vez;
6. Cada folha contém, ao final, os pagamentos resultantes a cada participante do jogo;
7. E, por fim, a descrição completa da árvore é de conhecimento comum a todos jogadores. Ou seja, cada um sabe o que os outros também sabem (2).

Tantos os jogos cooperativos como os não-cooperativos - duas das principais divisões dos modelos de jogos teóricos que são abordadas a seguir - podem ocorrer em condições cujas tomadas de decisões dos participantes são feitas simultaneamente, em sequência ou a cada vez que os jogos são repetidos. Os jogos simultâneos são aqueles em que as escolhas das estratégias acontecem ao mesmo tempo, sendo de preferência representados por matrizes. Quando a ordem de atuação influencia o seu desenvolvimento, os jogos são chamados sequênciais. Nos jogos sequenciais finitos, a melhor forma de representação se dá por meio do esquema de árvores. Por fim, os jogos repetidos exigem que as mesmas opções de estratégias sejam exibidas em rodadas sucessivas, nas quais os jogadores têm de decidir novamente se mantêm suas escolhas anteriores ou trocam de alternativa. A iteração que ocorre nos últimos faz surgir misturas de estratégias que não poderiam levar a uma solução equilibrada, quando jogadas de uma única vez, na condição pura do jogo base apresentado na primeira rodada. Jogos repetitivos também são chamados de superjogos. Nos superjogos, a memória exerce um papel crucial na construção de um equilíbrio que se torna muito difícil quando as ações dos jogadores não são plenamente recordadas ou são perturbadas pelo acaso. Os superjogos servem de base aos modelos de simulação utilizados em larga escala pela biologia, ciência da computação e ciências, em geral.

Informações

Conforme a possibilidade ou não de comunicação e a quantidade de informação acessível, os jogos podem ser divididos em cooperativos ou não-cooperativos, de informação completa ou incompleta, perfeita ou imperfeita. Jogos cooperativos são aqueles em que a comunicação prévia é permitida entre os jogadores, antes de decidirem a estratégia que adotarão durante o jogo. Com isso, acordos irrevogáveis e auto-motivantes são passíveis de estabelecimento. Para ser eficaz, a comunicação precisa ser livre de distorção e sem qualquer custo para os falantes, isto é, a emissão de mensagens não implica em uma alteração direta da matriz original do jogo. Entretanto, embora a comunicação, à primeira vista, pareça facilitar a realização de contratos, também abre espaço para imposição de coalizões, ameaças e blefes que perturbam a produção dos melhores resultados para uma das partes. Uma visão mais abrangente do papel da comunicação será discutida de perto na próxima unidade, toda dedicada a esse tema importante para a Teoria dos Jogos.

Jogos não-cooperativos proíbem que a comunicação prévia seja estabelecida, apesar de haver situações em que a sinalização acontece, bem como o encontro de convenções que ajudam a coordenar as ações dos agentes, com base no conhecimento comum partilhado pela cultura, convívio social ou capacidade cognitiva dos jogadores. Nestas ocasiões, um efeito chamado de "telepatia" emerge como forma de comunicação implícita entre falantes de uma mesma língua ou habitantes de uma mesma região ou grupo social, dotados de mentes semelhantes e conhecimento comum.

De todo modo, sendo ou não implementada a comunicação, quando os jogadores têm pleno conhecimento do número de participantes, da posição que cada um ocupa em cada etapa do jogo e dos resultados que todos podem obter, diz-se que o jogo é de informação completa. Na falta de um desses elementos informativos, o jogo é de informação incompleta e as características sobre o tipo dos jogadores deixam de ser de conhecimento comum, quebrando a simetria entre eles. Em jogos de informação perfeita, por meio de indução reversa, os jogadores podem conhecer toda história do jogo, antes mesmo de tomarem suas decisões. Todos conjuntos de informação de uma árvore de jogo de informação perfeita são unitários. O que vale dizer que cada parte sabe em qual nó de um jogo sequencial está. Caso contrário, o jogo é chamado de informação imperfeita. Os participantes que se lembram, a cada rodada, de todos os lances anteriores efetuados desde o início do jogo possuem memória perfeita, enquanto nos jogos em que não é possível ter toda essa informação do passado são chamados de memória imperfeita.

Uma maneira de trabalhar a falta de informações na modelagem dos jogos é introduzir a natureza como uma parte atuante em alguma jogada. Assim, as incertezas dos demais jogadores, em relação à definição das regras, podem ser interpretadas como probabilidades subjetivas, que a psicologia dos jogadores trata de estabelecer. Em diversos textos do final dos anos 1960 - onde se destaca "Games with Incomplete Information Played by 'Bayesian' Players" ("Jogos com Informação Incompleta Jogados por 'Bayesianos'", 1967-68) -, John Harsanyi sistematizou essa situação tratando os agentes como jogadores "bayesianos", isto é, aqueles cujas incertezas podem ser operadas através de uma distribuição da probabilidade subjetiva conjunta partilhada por todos (3). Embora a aplicação destas idéias seja díficil de ser observada por humanos e outros animais no seu dia-a-dia, o modelo de Harsanyi serviu para descrever as circunstâncias em que a informação é assimétrica, quando alguém dispõe de um conhecimento privilegiado sobre os ingredientes do jogo que não é de domínio dos outros envolvidos na mesma situação dos jogos chamados de informação incompleta. De uma certa forma, também foi uma resposta à proposta feita por Thomas Schelling no segundo apêndice de The Strategy of Conflict (A Estratégia do Conflito) para o abandono da simetria na Teoria dos Jogos. A adoção desta sugestão trazia algumas dificuldades para a teoria, uma vez que o equilíbrio de Nash tinha como condição a simetria entre os jogadores, apesar da maioria dos casos interessantes envolver movimentos assimétricos. A solução de Harsanyi produziu, então, equilíbrios Bayes-Nash para cada tipo de jogador que maximiza os valores esperados de acordo com as estratégias seguidas pelos outros, subentendendo a incerteza quanto ao tipo do outro jogador, que pode ser diferente tendo em vista a crença subjetiva na probabilidade prévia de distribuição desses tipos na natureza (4). A crença prévia comum é a expectativa que todos jogadores têm sobre o modo da natureza produzir alternativas de forma aleatória. Tal crença nada mais é, portanto, que o conhecimento comum da probabilidade estimada de que um tipo de jogador venha fazer parte do jogo. De posse dessas informações os jogadores podem avaliar suas escolhas a partir de probabilidades predeterminadas de que esteja enfrentando um tipo diferente ou semelhante de respectivos oponentes. Toda essa discussão, entretanto, depende da maneira que a comunicação é tratada, tema que será mais desenvolvido na segunda unidade deste curso.

Soma Zero ou Variável

Jogos não-cooperativos incluem, entre outras, uma categoria de confronto de interesses que é definida como estritamente competitiva. São situações extremas nas quais para um jogador ganhar o outro tem necessariamente de perder, ou então as partes terminam o jogo sem saldo algum. Nos assim chamados jogos de soma zero, não há possibilidade de cooperação entre dois agentes egoístas, já que seus interesses são totalmente opostos. Contudo, com mais de duas pessoas, coalizões de jogadores podem ser formadas contra a outra parte, motivo pelo qual os jogos passam a ser considerados cooperativos, admitindo a influência da comunicação prévia. Não obstante, a soma dos resultados de todos os jogadores envolvidos nessa interação é sempre igual a zero. Na matriz de jogos de duas pessoas e soma zero, por convenção omitem-se os ganhos relativos à coluna, que passam a ser inferidos a partir do resultado expresso para a linha, multiplicado por menos um (figura 3).

Figura 3 - Matriz de Jogo de Soma Zero	Estratégias	Coluna
		Pedra	Papel	Tesoura
Linha	Pedra	0	-1	1
	Papel	1	0	-1
	Tesoura	-1	1	0
O tradicional Pedra, Papel ou Tesoura (originário do Japão) é um típico jogo simultâneo de soma zero. Quem escolhe a estratégia "pedra" (mão fechada) quebra "tesoura" (dedos indicador e médio abertos), empata com "pedra" e perde de "papel" (mão aberta). "Papel" cobre a "pedra", empata com "papel" e perde de "tesoura". Esta, por fim, corta "papel", empata com "tesoura" e perde de "pedra".

De acordo com o teorema de Zermelo, publicado em 1913, no artigo "Uber eine Anwendung der Mengenlehre auf die Theorie des Schachspiels" (Sobre uma Aplicação da Doutrina Mista à Teoria do Jogo de Xadrez), jogos finitos de soma zero com informação perfeita são estritamente determinados. Qualquer um dos jogadores tem a sua disposição uma estratégia capaz de garantir a vitória, ou ao menos o empate, a despeito de como o adversário atuará. Tal pressuposto pode ser demonstrado por contradição: ao admitir-se que um jogo soma zero finito, com informação perfeita, não é estritamente determinado, deve-se supor que nenhum jogador possui uma linha de ação que, desde o início do jogo lhe traga a vitória, posto que, do contrário, o oponente não poderia encontrar outra que o permitisse vencer. Assim, o primeiro lance do jogo não será uma posição vitoriosa, qualquer que seja a posição inicial. Caso houvesse, o primeiro jogador mover-se-ia imediatamente para lá. Além disso, tal posição também não será vitoriosa para o adversário, pois se fosse assim teria desde o início condições de ganhar o jogo.

Por conseguinte, se a primeira jogada não assegura vitória, a segunda também não a garante, muito menos as demais, até o infinito. Contudo, se o jogo é finito, tem de haver uma posição final, na qual um dos jogadores alcance a vitória ou o empate. Logo, a condição da finitude do jogo contradiz a afirmação de que o jogo não é estritamente determinado, demonstrando, então, a validade do Teorema (5).

Pedra, Papel ou Tesoura não é um jogo estritamente determinado por ser simultâneo e, portanto, de informação imperfeita, pois, qualquer estratégia que venha a ser adotada pode ser vencida por uma outra adequada do adversário. Ambos escolhem suas ações ao mesmo tempo, sem saber qual será a decisão do outro, o que torna impossível uma solução usando apenas as estratégias puras. Não há, como se verá mais adiante, uma estratégia dominante, ponto de sela, ou equilíbrio entre as opções dos jogadores nessa circunstância. Já o xadrez - aquele jogo "sem graça" -, tal como o jogo da velha, é estritamente determinado.

Os jogos de soma zero tiveram sua análise esgotada em Theory of Games and Economic Behavior, de John von Neumann e Oskar Morgenstern. E durante o curto período que antecedeu a tese de John Nash, mesmo os jogos de soma diferente de zero poderiam ser tratados como de soma zero, bastando para tanto, introduzir um jogador a mais que assumisse as perdas da totalidade ganha pelos outros jogadores. Como propunham Von Neumann e Morgenstern, esse jogador "não teria influência direta no curso do jogo" (6). Seu papel, embora fictício, muitas vezes poderia ser associado à função exercida pela natureza, ou o tesouro nacional de um país qualquer, nos jogos de uma ou mais pessoas em que os recursos naturais ou monetários são partilhados pelos jogadores que tomam a decisão de dividir esses bens entre si. Nesses casos, a natureza ou o tesouro assumiriam os prejuízos ou absorveriam os excedentes gerados pela interação dos demais jogadores. Muitos autores consideram a redução dos modelos de jogos à soma zero de pouca utilidade para as ciências sociais, pois, como lembra Silvia Nasar, "até mesmo na guerra há, quase sempre, algo a ser obtido da cooperação" (7). Não obstante essas opiniões, reconhecer jogos de soma zero, numa escala mais ampla, ajuda a entender melhor os problemas ambientais, na perspectiva da tragédia dos comuns apresentada pelo biólogo Garrett Hardin (1915-2003) no artigo The Tragedy of the Commons (A Tragédia dos Comuns, de 1968.

Hardin imaginou a situação de pecuaristas que mantêm a maior quantidade de gado possível em terras devolutas, sem dono, mas de uso comum. Tudo vai bem enquanto o crescimento vegetativo da população fica abaixo da capacidade da terra se recuperar. Porém, paradoxalmente, quando as metas de bem estar social conseguem tornar prósperas as vidas das pessoas, o número crescente de gado no pasto, acaba por levar à ruína os criadores que buscam maximizar o seu ganho com a venda de carne ou leite, uma vez que o custo de manutenção de cada animal não pode mais ser suportado pelos recursos "gratuitos", mas limitados da natureza (8). O mesmo acontece com o crescimento populacional, a poluição, a devastação das florestas e todo tipo de ação que vise tirar proveito das externalidades dos bens públicos. Assunto a ser discutido na segunda unidade da seção II, deste curso.

Não obstante, jogos que não são estritamente competitivos permitem aos participantes preferirem opções que não estão em total oposição entre eles. Um jogador pode desejar obter um resultado que o favoreça, sem necessariamente causar prejuízo ao outro. O que não é possível em jogos de duas pessoas e soma zero. Ademais, jogos de soma variante, diferente de zero, ao serem repetidos várias vezes podem promover a cooperação, apesar de nenhuma comunicação prévia ter ocorrido. Através de vias indiretas, como a sinalização, convenções ou encontro de pontos focais, tacitamente, as escolhas de estratégias favoráveis entre as partes acontecem assim que uma solução única se mostre distinta a todos de modo semelhante.

Ao contrário dos jogos de soma zero, onde uma solução direta é passível de ser encontrada por meio de estratégias minimax, ou maximin - abordadas no próximo ponto -, os de soma variável apresentam características de competição e cooperação que dificultam bastante a busca de uma solução que seja aplicável a todos os casos. Sem embargo, a abordagem ampla de jogos não estritamente competitivos e de soma diferente de zero só foi possível depois de John Nash ter descoberto para os jogos não-cooperativos uma solução geral que abrangeu também os cooperativos. Enquanto nos jogos cooperativos os acordos obtidos tornavam obrigatória sua execução, nos jogos não-cooperativos não fica claro se os contratos possíveis serão cumpridos, em parte ou em sua totalidade, como ocorre quando se defrontam seres egoístas, dotados de racionalidade instrumental, que usam de qualquer meio para satisfazerem seus interesses imediatos. A prova da existência de um ponto de equilíbrio, do qual nenhum jogador poderia fugir unilateralmente sem afetar o resultado do outro, serviu não só para resolver os problemas formais restritivos da Teoria dos Jogos cooperativos, mas fez com que as ciências sociais pudessem aplicar esse tipo de ferramenta de análise fora dos domínios da economia e da matemática.

De qualquer maneira, todos os jogos proporcionam a oportunidade de avaliar formalmente a relação das listas de preferências manifestas, de duas ou mais pessoas. Contudo, durante o desenrolar das partidas, aspectos psicológicos estão a todo momento ameaçando a manutenção da racionalidade estratégica pressuposta pela Teoria da Utilidade adotada no modelo de jogos. Utilidade é um dos diversos termos da teoria que causam confusão entre os filósofos, uma vez que a moderna teoria da utilidade traçada por Von Neumann e Morgenstern difere em muitos pontos da antiga noção de utilidade que subjaz, principalmente, ao Utilitarismo dos seguidores de Jeremy Bentham (1748-1832) - sobretudo o caráter moral que obrigaria aos governos maximizar a utilidade da maioria da população, a grosso modo, sem considerar os ganhos individuais em primeiro lugar (9).

Utilidade

Tudo que Von Neumann e Morgenstern pretendiam construir com o livro de 1944 era um mero procedimento matemático que pudesse servir como instrumento de análise de situações em que se pode comparar as utilidades das pessoas envolvidas. Em outras palavras, o problema da comparação das utilidades era visto como uma tentativa de avaliar o conjunto de possibilidades de atuação de um agente (indivíduo ou grupo), com objetivo de maximizar ou minimizar a sua satisfação ou frustração, segundo uma lista de preferências. O que não quer dizer que a maximização da utilidade tenha de contemplar apenas interesses mesquinhos ou egoístas, no sentido de exclusividade. Irmã Dulce (1914-1992) ou a Madre Teresa de Calcutá (1910-1997), ao buscarem fornecer o máximo de recursos aos pobres e miseráveis, no Brasil e na Índia, respectivamente, estavam também, do ponto de vista da teoria dos jogos, maximizando seus próprios interesses. Como diria o psicólogo e matemático canadense Anatol Rapoport, "não há contradição entre esse impulso de caridade e a maximização da utilidade" (10). Assim, para a Teoria dos Jogos, a utilidade nada mais é do que uma unidade de medida padrão expressa em util (no plural, utiles) ou valores monetários.

Quanto às circunstâncias em que são feitas, a seleção da linha de ação que será adotada faz-se sob condições de certeza, risco, incerteza ou, como Duncan Luce e Howard Raiffa acrescentaram, à luz de evidências empíricas que misturam risco e incerteza (11). Num cenário de certeza, sabe-se que cada ação conduzirá invariavelmente a um resultado específico. Sob risco são tomadas as decisões cujas ações levam a um dos possíveis resultados esperados a uma taxa de probabilidade conhecida - como os 50% de chances de sair ou cara ou coroa no lançamento de uma moeda ao ar. A incerteza diferencia-se do risco pelo fato da probabilidade não ter uma proporção fixa predeterminada - as chances de chover amanhã, por exemplo. Para que as escolhas sejam plausíveis, um conjunto de axiomas propostos por Von Neumann e Morgenstern e sustentado por vários autores postula, em geral, que haja pelo menos:

1. ordenamento das alternativas;
2. transitividade das preferências;
3. continuidade;
4. combinação e substituição delas por chances de obtenção de um ganho ao qual se é indiferente.

O ordenamento das preferências, ou indiferença, exige que o jogador prefira uma oportunidade a outra ou seja indiferente às duas. Assim, para o teórico dos jogos não haveria coisa alguma que não fosse passível de comparação com outro objeto, alvo de crença ou desejo. Na comparação entre objetos, sorteios compostos, nos quais se passa de um sorteio para o outro, podem ser reduzidos a uma simples loteria em que a probabilidade final de alcançar um resultado incorpora as chances de cada ramo que traça o caminho que leva até o nó terminal, na forma extensiva. A transitividade das preferências e indiferenças das coisas e loterias é uma relação que evita a circularidade e inconsistência que tornariam praticamente intratável a teoria da utilidade. Pois, se alguém prefere "A" a "B" (A > B) e "B" a "C" (B > C), conclui-se que também prefira "A" a "C" (A > C), ou seja indiferente caso haja indiferença entre "A" e "B" (A = B) e "B" e "C" (B = C). Se a probabilidade de ganhar algo desejado for indiferente à posse de um outro objeto de ganho certo, o jogador deverá arriscar-se ao sorteio sempre que existir um número racional entre 0 e 1 ao qual se esteja indiferente entre uma loteria que envolva o objeto mais querido e a posse de outra coisa inferior. O que, em resumo, equivale à existência de uma continuidade na lista de preferências de um agente e um ponto em que se possa estabelecer comparações entre elas: "tudo tem seu preço". Por conseguinte, exige-se que um sorteio possa ser substituído por outro, exceto no caso de alternativas relevantes. Ou seja, um jogador que se mostrar indiferente entre um prêmio novo e o anterior, também deverá sê-lo quando duas outras loterias nas mesmas condições forem propostas. Tal pressuposto é conhecido ainda como a hipótese de independência das alternativas relevantes, ponto crucial na discussão que o economista francês Maurice Allais estabeleceu em 1953. Afinal, havendo a possibilidade de mais de um sorteio ocorrer, aquele cuja probabilidade de obtenção de algo que seja melhor for maior deverá ser o escolhido, de acordo com uma última condição chamada monotonicidade.

A função de utilidade, portanto, faz a associação de números às preferências e às circunstâncias em que a sorte leva a resultados finais almejados. Ela permite a comparação das utilidades de diferentes pessoas como medidas intervalares de escalas diferentes ou mesmo desconhecidas. Como explica Rapoport, o ponto zero e a unidade das escalas podem ser arbitrários, bastando apenas a determinação da proporção de cada par de diferenças da utilidade, do mesmo modo que se comparam as escalas de temperatura, seja em graus Celsius, Fahrenheit ou Kelvin (12). Entretanto, a pretensão de quantificar qualquer objeto que seja alvo do interesse de um agente, incluindo sentimentos subjetivos, abriu espaço para diversas especulações, apoiadas em experimentos laboratoriais e de campo. Allais argumentou que indivíduos, em geral, não consideram as probabilidades objetivas em suas decisões, mas adotam probabilidades subjetivas, representações psicológicas, quando defrontados a situações de risco. Na prática, isso poria abaixo os axiomas de independência forte ou substituição.

Entre escolhas de ganhos certos e indeterminados como neste exemplo em que a...

1. certeza de receber 100 milhões ou a
2. probabilidade de 10% de ganhar 500 milhões e 89% de ganhar 100 milhões e 1% de nada obter;

3. ganhar 100 milhões a 11% e 89% de nada ganhar ou
4. 10% de ganhar 500 milhões e 90% de obter zero

100 milhões para "A"; 139 milhões para "B"; 11 milhões para "C" e 50 milhões para "D".

O que significa que a relação de preferências entre esses resultados não preserva os mesmos valores em circunstâncias objetivamente semelhantes, pois o desejo pelo ganho certo que a maioria das pessoas manifesta, quando indica "A > B", não se repete na variação presente em "C > D", cuja diferença de 39 milhões é igual nas duas loterias apresentadas (13).

Este exemplo fornecido por Allais apontou para uma forte deformação provocada pelos valores psicológicos sobre a expectativa de resultados, cuja pretensão de satisfação absoluta da utilidade, através de escolhas aleatórias, se mostrou inviável, devido aos desvios empreendidos às estratégias preferidas na presença de fatores de risco. Os componentes psicológicos, que tanto influenciam as decisões corretas, tiveram então de serem melhor avaliados pelos psicólogos e teóricos dos jogos que, embora reconhecessem as dificuldades de formalização do processo amplo de deliberação que envolve os sentimentos emersos de cenários incertos, percebiam que suas principais falhas recaíam sobre a descrição da condição natural do agente e não sobre o método de axiomatização, propriamente dito, empregado na teoria. As tentativas de Harsanyi ou Kahneman e Tversky, para citar apenas os laureados com Nobel, ajudaram a traçar com maior precisão a maneira adequada de se chegar a uma solução com o uso do cálculo das probabilidades e com a percepção dos efeitos da aversão e busca do risco nos casos de ganhos e perdas, respectivamente. Problemas que serão examinados logo depois de outros conceitos básicos sobre estratégias terem sido expostos no próximo texto.

Notas
1. Veja SHUBIK, M. Teoría de Juegos en las Ciencias Sociales, III.3.1 a III.3.3, pp. 48-53.
2. Veja HART, S. "Games in Extensive and Strategic Forms", in AUMANN, R. & HART, S. Handbook of Game Theory with Economic Application, vol. 1, cap. 2, § 1, pp. 22/5.
3. Harsanyi aplicou em três artigos sucessivos chamados “Game with Incomplete Information Played by ‘Bayesian’ Players” a estatística bayesiana em jogos em que os participantes não são totalmente informados e têm incerteza quanto aos resultados obtidos, com intuito de achar uma solução racional para esses casos. A contribuição de Thomas Bayes (1702-1761), neste caso, resume-se ao seu método de encontrar a probabilidade de ocorrência de determindas causas, antes do evento qualquer ser observado. Pelo teorema de Bayes, a probabilidade (P) de uma hipótese (h), ou informação, dividida por sua evidência (e), ou evento, é igual ao produto das probabilidades da hipótese e da evidência dividida pela hipótese, sendo o resultado uma fração da probabilidade da evidência, ou P(h/e) = [P(h) × P(e/h)] ÷ P(e). Tudo isso, é claro, na suposição de que existam seres vivos capazes de respeitar a regra de Bayes.
4. Veja SCHELLING, Th. C. The Strategy of Conflict, ap. B, pp. 277 e ss; VARIAN, H. R. Intermediate Microeconomics, cap. 15, §§ 15.12-13, pp. 279/82 e FIANI, R. Teoria dos Jogos, cap. 7, pp. 175 e ss. para introdução ao assunto.
5. Veja DAVIS, M. Teoria dos Jogos, cap. 2, apêndice, p. 32/4.
6. VON NEUMANN, J. & MORGENSTERN, O. Theory of Games and Economic Behavior, § 56.2.2, p. 506.
7. Veja NASAR, S. Uma Mente Brilhante, cap. 9, p. 120.
8. Veja HARDIN, G. "The Tragedy of the Commons".
9. O que não impediu o psicólogo Daniel Kahneman de tentar uma aproximação entre os dois conceitos no artigo "Experienced Utility and Objective Happiness" (2000), incluído na coletânea KAHNEMAN, D. & TVERSKY, A. Choice, Values and Frames, bem como Harsanyi de defender a validade do utilitarismo frente a outras teorias morais, com base na teoria dos jogos (em HARSANYI, J. "Game and Decision Theoric Models in Ethics").
10. RAPOPORT, A. Lutas, Jogos e Debates, part. II, cap. VI, p. 97.
11. De acordo com LUCE, R. D. & RAIFFA, H. Games and Decisions, § 2.9, p. 37.
12. Veja RAPOPORT, A. Op. cit., part. II, cap. VI, pp. 98 e ss. para conhecer essa passagem e os detalhes do exemplo esclarecedor da temperatura.
13. Veja ALLAIS, M. F. Ch. "Le Comportement de l'Homme Rationnel Devant le Risque", p. 527.

ALLAIS, M. F. Ch. "Le Comportement de L'Homme Rationnel Devant le Risque". Econometrica, vol. 21, n° 4, pp. 503-546, outubro. 1953.

AUMANN, R & HART, S. Handbook of Game Theory with Economic Application, vol. 1. – Amsterdam: Elsevier Science, 1992.

DAVIS, M. D. Teoria dos Jogos; trad. Leonidas Hegenberg e Octanny S. da Mota. – São Paulo: Cultrix, 1973.

FIANI, R. Teoria dos Jogos. - Rio de Janeiro: Elsevier, 2004.

HARDIN, G. "The Tragedy of the Commons", Science, n° 162, pp. 1243-1248, 1968. Disponível na Internet via http://dieoff.org/page95.htm. Arquivo consultado em 2004.

HARSANYI, J. "Game and Decision Theoric Models in Ethics", in AUMANN, R & HART, S. Handbook of Game Theory with Economic Application, vol. 1, cap. 19. – Amsterdam: Elsevier Science, 1992. pp 669-707.

KAHNEMAN, D. "Experienced Utility and Objetive Happiness", in KAHNEMAN, D & TVERSKY, A. Choice, Values and Frames, cap. 37, pp. 673-692. –Nova York: CUP, 2000. Disponível na Internet via http://www.international.ucla.edu/cms/files/Kahneman.pdf. Arquivo consultado em 2004.

KAHNEMAN, D. & TVERSKY, A. "Prospect Theory". Econometrica, vol. 47, n° 2, pp 263-291, março. 1979.

KREPS, D. M. Game Theory and Economic Modelling. – Oxford: OUP, 1996.

LUCE, R.D. & RAIFFA, H. Games and Decisions. - Nova York: Dover, 1989.

NASAR, S. Uma Mente Brilhante; trad. Sérgio M. Rego. –Rio de Janeiro: Record, 2002.

NASH, J. "The Bargaining Problem", in KUHN, H. & NASAR, S. The Essential John Nash. - Princeton: PUP, 2002.

______. "Equilibrium Points in n-Person Games", in KUHN, H. & NASAR, S. The Essential John Nash. - Princeton: PUP, 2002.

______. "Non-Cooperative Games", in KUHN, H. & NASAR, S. The Essential John Nash. - Princeton: PUP, 2002.

______. "Two-Person Cooperative Games", in KUHN, H. & NASAR, S. The Essential John Nash. - Princeton: PUP, 2002.

Von NEUMANN, J. & MORGENSTERN, O. Theory of Games and Economic Behavior. – Princeton: PUP, 1953.

RAPOPORT, A. Lutas, Jogos e Debates; trad. Sérgio Duarte. – Brasília: UnB, 1980.

ROSS, D. "Game Theory", in Stanford Encyclopedia of Philosophy. Disponível na INTERNET via http://plato.stanford.edu/entries/game-theory/. Arquivo consultado em 2001.

SCHELLING, Th. C. The Strategy of Conflict. – Nova York: OUP, 1963.

SHUBIK, M. Game Theory in the Social Sciences. – Cambridge (Ma.): MIT, 1982. Ed. mexicana Teoría de Juegos en las Ciencias Sociales; trad. Catalina D. Reyes. – México, D.F.: Fondo de Cultura Económica, 1992.

Da SILVA, A. R. A Voz do Outro. – Rio de Janeiro: UFRJ/IFCS, 2003. Tese (Doutorado em Filosofia).

SIMONSEN, M. H. "Teoria dos Jogos". Ensaios Econômicos, n° 159, pp. 1-74. - Rio de Janeiro: FGV, 1990.