* Número PI *

Escola Estadual Gastâo da Cunha - Contagem - MG

[Principal] [Fractais] [Logaritmos][Matriz 3x3] [Matriz Inversa] [Eq.2o.Grau] [Matemática]

Histórico

O cálculo do número Pi  desafiou os matemáticos , desde as eras mais remotas .Pi, ou P, é a relação entre a circunferência e o seu diâmetro. E  a fórmula que o representa é :

Desta fórmula obteremos outra:

     Utilizando computadores, os matemáticos conseguiram calcular o valor de P até 100.000 casas decimais. Porém, Pi é um número irracional (e existem infinitas casas decimais ) .

    O p também é utilizado para se descobrir a área, a circunferência ou o raio de objetos redondos, como a Terra .

    Pode-se obter na prática  o valor de p medindo com um barbante o perímetro de um Pneu de bicicleta  e dividi-lo pelo seu diâmetro (duas vezes o raio).

Um papiro egípcio de cerca de 1.500 a.C (o Papiro de Rhind) mostra que os egípcios utilizavam o p como sendo 3,16.

    OS egípcios conseguiram uma aproximação melhor que a dos babilônios, que afirmavam :"o comprimento de qualquer circunferência era o triplo de seu diâmetro" .

Por volta do século III a.C., Arquimedes - o mais famoso matemático da Antiguidade, também procurou calcular a razão entre o comprimento de uma circunferência e o seu diâmetro. Começando com um hexágono regular , dobrou sucessivamente o número de lados até obter um polígono com 96 lados (6,12,24,48 e 96 lados) .

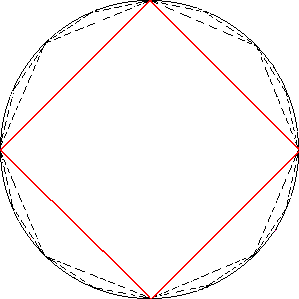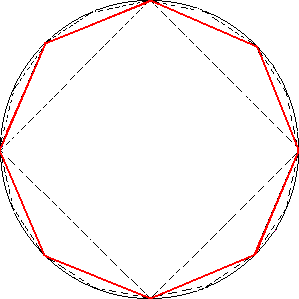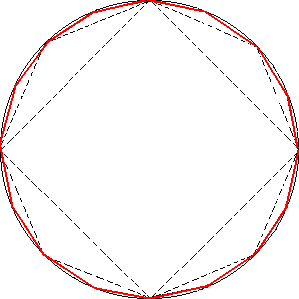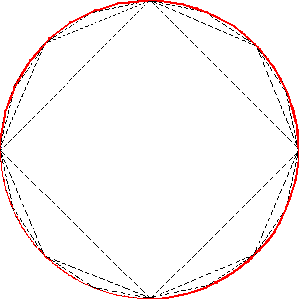
    Analogamente a partir de um quadrado poderemos dobrar o número de lados até obter uma figura com (4,8,16,32,64,128... lados)

     Calculando o perímetro do polígono de 96 lados, conseguiu para pi um valor entre 3,1408 e 3,1428.

    Com um polígono de 720 lados inscrito numa circunferência de 60 unidades de raio, Ptolomeu conseguiu calcular o valor de pi como sendo 377/120, que é aproximadamente igual a 3,1416 (aproximação melhor que a de Arquimedes) .

    O fascínio pelo cálculo do valor exato de pi também tomou conta dos chineses. No século III d.C., Liu Hui, um copiador de livros, conseguiu obter o valor 3,14159 com um polígono de 3 072 lados.

    No fim do século V, o matemático Tsu Ch'ung-chih foi mais longe ainda: encontrou como valor de pi um número entre 3,1415926 e 3,1415927.

Nesta época, o grande matemático hindu Aryabhata deixou registrada esta afirmação num pequeno livro escrito em versos:

"Some-se 4 a 100, multiplique-se por 8 e some-se 62 000. O resultado é aproximadamente uma circunferência de diâmetro 20 000".

Se você recordar que o comprimento de uma circunferência é dado por c = pi . d, fica fácil entender que a solução da equação de Aryabhata:

(4 + 100) . 8 + 62 000 = pi . 20 000

104 . 8 + 62 000 = pi . 20 000

832 + 62 000 = pi . 20 000

62 832 = pi . 20 000

62 832/20 000 = pi

indica como valor de pi 3,1416.

62 832/ 20 000= 3,1416

Quanto maior o número de casas decimais, melhor é a aproximação que se obtém para pi.

Até o século XV, o melhor valor para pi havia sido encontrado pelo matemático árabe al-Kashi: 3,1415926534897932.

Mas o cálculo mais impressionante foi efetuado pelo matemático holândes Ludolph van Ceulen (1540-1610) no final do século XVI.

Começando com um polígono de 15 lados e dobrando o número de lados 37 vezes, Ceulen obteve um valor para pi com 20 casas decimais.

Logo em seguida, usando um número de lados ainda maior, ele conseguiu uma aproximação com 35 casas decimais!

Sua esposa mandou gravar no túmulo o valor de pi com as 35 casas decimais como homenagem.

No final do século XX computadores calculariam, em segundos, o valor de pi com 100, 1000, 10 000, milhões de casas decimais!

Pi = 3,14159265358979323846264 33832795028841971693993751058 20974944592307816406286208998 62803482534211706798214808651 32823066470938446095505822317 253594081128481117450284102701 93852110555964462294895493038 19644288109756659334461284756 48233786783165271201909145648 5669234603486104543266482...

Cálculos

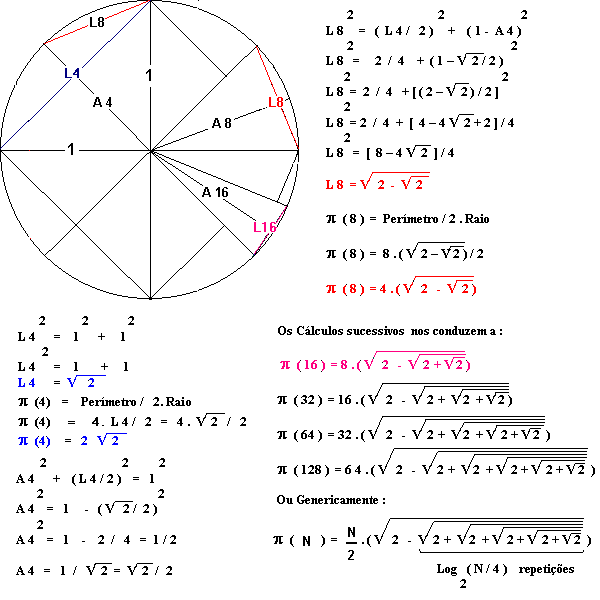
Utilizando os Cálculo efetuados acima poderemos calcular o valor aproximado de PI :

Podemos indicar o número de lados de um polígono qualquer , aproximarmos para um polígono cujo número de lados é múltiplo de 4  e calcularmos o seu perímetro: 

Insira o Número de lados de um polígono qualquer

o número de lados do polígono ( + próximo >> )

Achamos o valor aproximado de PI  para este polígono usando sucessivas iterações :

[Principal] [Fractais] [Logaritmos][Matriz 3x3] [Matriz Inversa] [Eq.2o.Grau] [Matemática]