- Propiedades básicas de los fractales -
Todo el tratamiento de las propiedades se podría hacer para cualquier conjunto fractal, no obstante, el que consideramos de mayor nivel didáctico, es el conjunto de Cantor. Por lo tanto, este será el fractal a tratar como exposición de las propiedades, ejemplificándolas a su vez con otros fractales.
La idea de este concepto es asequible tras considerar el siguiente ejemplo:
Tomamos el valor inicial 1. Ahora lo multiplicamos por 2. Nos da como resultado el número 2. Tomamos el resultado como valor inicial. Lo multiplicamos por 2. Nos da 4. Así, sucesivamente, vamos aplicando este procedimiento. Gráficamente, podríamos verlo de esta forma:
........
Esto podríamos resumirlo de forma general en el siguiente gráfico:
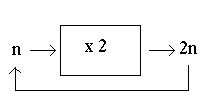
Es decir, tomamos un valor inicial, lo multiplicamos por 2, y el resultado que nos ha dado lo tomamos como valor inicial. Ahora, con el nuevo valor inicial, volvemos a aplicar el proceso.
Vamos a considerar este ejemplo de forma más general. Tomamos un valor inicial. A este valor inicial le aplicamos una cierta regla. Tras aplicar esta regla, obtenemos un resultado. Tomamos este resultado como valor inicial, y le aplicamos esa cierta regla. Vamos repitiendo el proceso tantas veces como queramos. Gráficamente, esto puede verse así:
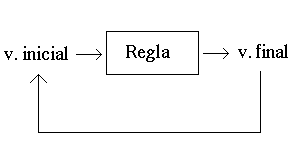
Ahora, vamos a ver esto con el conjunto de Cantor. Como hemos visto antes, la regla que se sigue para construirlo es "eliminar el tercio central de cada segmento". Vamos a ver esto en forma de diagrama:
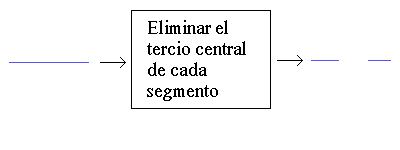
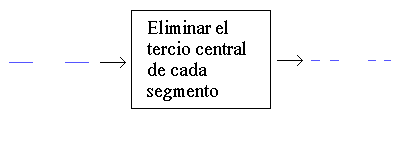
Siguiendo este esquema, repetimos el proceso tantas veces como queramos. Si este esquema es repetido infinitas veces, obtendremos el conjunto de Cantor.
Para afianzar esto, se proponen los siguientes ejercicios.
1. Dibuja el diagrama recursivo con el que construir el triángulo de Sierpinski hasta el cuarto paso. La regla es: "divide cada triángulo en cuatro triángulos iguales y elimina el central".
2. Haz lo mismo pero para el cuadrado de Sierpinski, hasta el cuarto paso. La regla es: "divide cada cuadrado en 9 cuadrados y elimina el cuadrado central.
En este apartado hay que hacer ver al alumno que la dimensión de un objeto fractal va a exceder de la dimensión esperada. Así, esta sería una forma alternativa de definir objeto fractal, como aquel cuya dimensión excede a la dimensión esperada.
Veamos ejemplos.
Conjunto de Cantor.
Se trata de un conjunto no numerable de puntos. Por tanto, la dimensión esperada sería 0, que es la dimensión de un punto, o de un conjunto de puntos. Sin embargo, su dimensión es aproximadamente 0.63, que es mayor que 0, pero menor que 1. Es decir, es algo más que un conjunto de puntos, pero menos que una recta.
Curva de Koch.
Se trata de una curva (con infinitos picos). Por tanto, la dimensión esperada sería 1, que es la dimensión de una curva. Pero tenemos que su dimensión es aproximadamente 1.26, que es mayor que 1, pero menor que 2. Es decir, es algo más que una curva, pero menos que un plano.
Triángulo de Sierpinski.
Se trata de un conjunto de lados de triángulos, es decir, un conjunto de rectas. Por tanto, la dimensión esperada es 1, que es la dimensión de una recta, o de un conjunto de rectas. Pero su dimensión es ln(3)/ln(2), que es mayor que 1. O sea, es algo más que un conjunto de rectas, pero no llega a ser un plano.
En este apartado, vamos a tratar de que el alumno sepa distinguir si una figura es, bien autosemejante, bien estrictamente autosemejante, o ninguno de los dos casos, y esto sólo puede conseguirse a base de ejemplos.
En primer lugar, es conveniente recordar la definición de autosemejanza, ya dada en el apartado "La dimensión no tiene por qué ser entera" (una parte es semejante al todo). Así, vamos primero a diferenciar bien entre una figura autosemejante y una figura estrictamente autosemejante. Para ello, tomamos como ejemplos la curva de Koch y la isla de Koch.
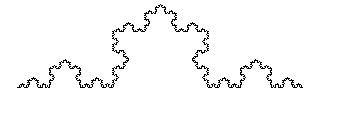
Primero consideremos la curva de Koch.
Si tomamos una parte cualquiera de esta curva, y la ampliamos, obtenemos de nuevo TODA la curva de Koch.
Por eso, podemos decir que la curva de Koch es estrictamente autosemejante.
Ahora, tomemos la isla de Koch.
Si tomamos un trozo cualquiera de dicha figura, se observa que es autosemejante a la figura total, pero esta vez NO se trata de una copia de la figura total a menor escala, pues si tomamos un trozo de la isla NO TENEMOS la isla entera.
Por tanto, aquí no podemos decir que la figura sea estrictamente autosemejante, aunque sí es autosemejante.
Podemos reflejar la idea, mediante ejemplos, que hay estructura fina, es decir, iterando una cantidad muy grande de veces seguimos obteniendo la misma estructura, la misma complejidad.
Hay que poner de relieve que esto no pasa si los objetos no tienen estructura fractal.
Por ejemplo, las siguientes figuras no son autosemejantes, y no son fractales:
Debe proponerse al alumno que den ejemplos, para comprobar que se ha comprendido correctamente el apartado.
También hay que hacer ver al alumno que en la naturaleza existen fractales autosemejantes, como los que a continuación mostramos en los dibujos :
NOTA: los dibujos a los que se refiere el texto son
imágenes de árboles generadas con el programa Fractal
Object Editor. Con este mismo programa se generaron imágenes
del mar, nubes y rocas. Espero poder poner en breve todas estas
imágenes, tan pronto como consiga de nuevo el programa
En este apartado lo que hay que dejar claro a los alumnos es que muchas estructuras fractales, debido a la autosemejanza, tienen "agujeros", "huecos", es decir, hay que conseguir que vean que estas estructuras son porosas. Para ello, nada mejor que mostrar la construcción de algunos conjuntos, para que vean como van aumentando los huecos a medida que avanzamos en dicha construcción. Además, dada una figura inicial, gráficamente puede apreciarse que de dos fractales distintos construidos sobre esta figura (por ejemplo, a partir de un triángulo, el triángulo de Sierpinski y una pequeña variación de este fractal) puede haber alguno que sea más poroso que otro, es decir, de forma intuitiva, que uno de ellos se vacía más rápidamente que el otro. Esta es la forma de determinar qué fractal es más poroso que otro.
A partir de las siguientes construcciones, el profesor puede preguntar al alumno cuál de cada pareja de fractales construidos bajo el mismo iniciador (un segmento, un triángulo, etc.. ) es más poroso.
Construcción del conjunto de Cantor.
Construcción de la variación del conjunto de Cantor.
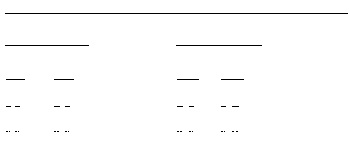
Construcción del triángulo de Sierpinski.
Construcción de la variación del triángulo de Sierpinski.
Construcción de la alfombra (el cuadrado de Sierpinski).
Construcción de la variación de la alfombra (la cruz).
|
|
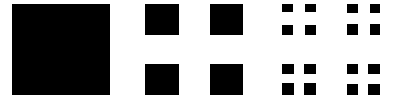
De vuelta a GeoCities