Fractales en la secundaria
- La técnica del Conteo de Cajas -
Hasta ahora hemos estudiado objetos fractales con la propiedad de autosemejanza. Pero sabemos que también hay objetos fractales sin esa propiedad (como por ejemplo costas, cuencas de ríos, árboles, etc..).

Para poder calcular su dimensión necesitamos usar otra técnica diferente a la ya conocida (n=(1/r)^D), pues no podemos encontrar una razón de semejanza ni n. Se trata del CONTEO DE CAJAS ocupadas. No es otra cosa que una herramienta que nos va a ser necesaria para calcular la dimensión de estos últimos objetos.

El método consiste en lo siguiente:

El objeto a medir se cubre con una malla formada por hipercubos encajados. Se cuenta el número total de hipercubos, y el número de hipercubos que contienen algún punto del conjunto a medir. Vamos variando la escala de la malla, haciéndola cada vez más pequeña, y repetimos el proceso con cada malla, unas 7 u 8 veces.
(Nota: aquí consideramos como hipercubo a las caras (n-1) dimensionales de un n-intervalo convenientemente elegido. En R^2 es el borde del cuadrado y en R^3 un cubo corriente).

Seguidamente, se plantea una tabla como la siguiente:
ln(1/escala) ln(n° hipercubos ocupados)
...... ......
...... ......

Calculamos los cocientes [ ln(n° hipercubos) ] / [ ln(1/escala) ], y, con ayuda de la calculadora, calculamos la pendiente de la recta que se ajusta a esos datos. El valor de esa pendiente es el valor de la dimensión.

Veamos, como ejemplo, cómo se calcula la dimensión de la costa de Inglaterra utilizando este método. Lo primero que hay que hacer es construir una tabla como la siguiente, contar las cajas ocupadas para cada escala, y rellenar la tabla con esos datos:
1/escala 4 8 12 16 24 32
Cajas ocupadas
Escala 1/4
Escala 1/8
Escala 1/12
Escala 1/16
Escala 1/24
Escala 1/32

Aquí aparecía el dibujo de la costa de Gran Bretaña recuadrado en mallas de 4x4, 8x8, 12x12, 16x16, 24x24, 32x32 cuadrados, con las escalas especificadas antes. En cuanto pueda pondré los gráficos.

Una vez contadas las cajas, se rellena la tabla :
1/escala 4 8 12 16 24 32
Cajas ocupadas 16 48 84 122 194 283

(Tabla 1)

Y una vez rellenada la tabla anterior, se completa la siguiente :
ln(1/escala) ln(n° hipercubos ocupados)
1.3862 2.7725
2.0794 3.8712
2.4849 4.4308
2.7725 4.8040
3.1780 5.2678
3.4657 5.6454

(Tabla 2)

Ahora, con la calculadora, vamos a ver cómo obtener la pendiente de la recta que se ajusta a los datos de la tabla 2.

Entrar en el modo regresión lineal, denotado LR. La columna ln(1/escala) son las x, la columna ln(n° hipercubos ocupados) son las y. Yendo de arriba a abajo, hacer:

Entrar x, pulsar tecla x D , y D. Entrar y, pulsa tecla DATA.

Una vez están todos los datos introducidos en la calculadora, pulsar INV B (esta B suele estar bajo el n° 8, pero puede variar según el modelo de calculadora), y el resultado que nos da es la pendiente que buscábamos, es decir, el valor de la dimensión del objeto estudiado, en nuestro caso, la costa de Gran Bretaña.

Y ese valor, siguiendo el procedimiento anterior, es : 1.37

Ahora que ya se sabe cómo utilizar esta técnica, es conveniente que el alumno resuelva el siguiente ejercicio.

Calcula, usando la técnica del conteo de cajas, la dimensión del siguiente objeto.

CURVA DE KOCH

Escala 1/4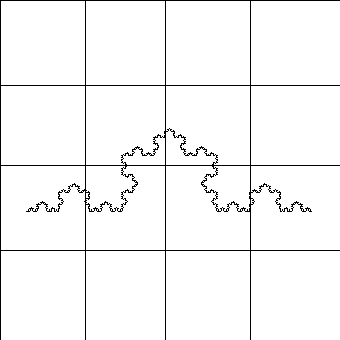
Escala 1/8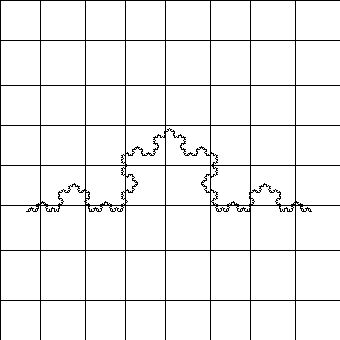
Escala 1/16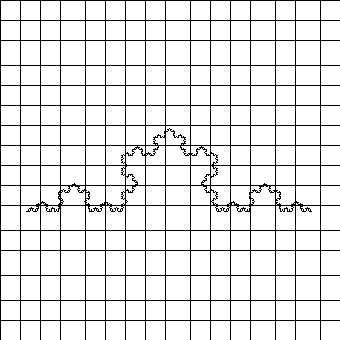
Escala 1/32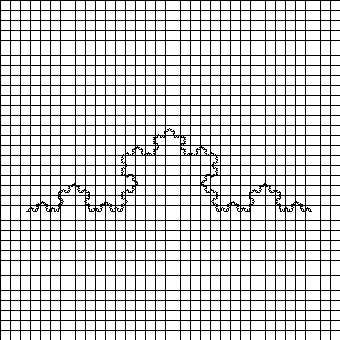

Página en construcción. Perdón por las molestias.

De vuelta a GeoCities