1-3
4-6
7-9
10-12
13-15
16-18
19-21
22-24
25-27
28-30
31-33
34-36
37-39
40-42
43-45
1-3
4-6
7-9
10-12
13-15
16-18
19-21
22-24
25-27
28-30
31-33
34-36
37-39
40-42
43-45



![]() 2
2![]() =
=![]() μ4
μ4
![]() s4
s4
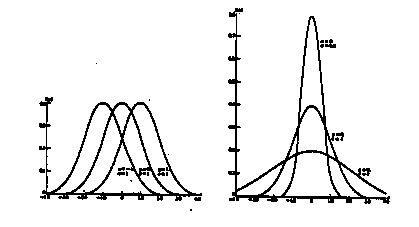
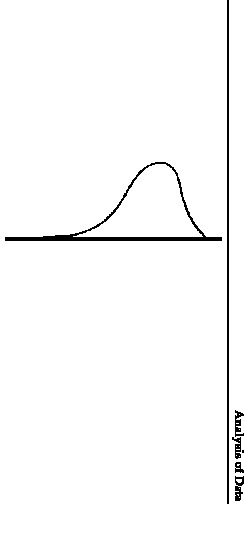
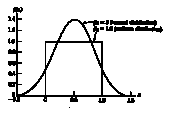
![]() Belowtwo probability densitiesare shown:
Belowtwo probability densitiesare shown:
![]() β
β![]() 2
2![]() for these two distributions are 1.8 and 3.0,
for these two distributions are 1.8 and 3.0,
![]() 4
4![]() =
=![]() ∑
∑![]() (x
(x![]() -
-![]() x
x



![]() x
x![]() < ∞
< ∞
![]() >
>![]() 0
0
![]() 1
1
![]() (
(![]() x)
x)![]() =
=![]() 1
1![]() e
e![]() -
-![]() (
(![]() s
s![]() -
-![]() μ
μ![]() )3
)3![]() / 2
/ 2![]() σ
σ![]() 2
2
![]() σ
σ![]() 2π
2π![]() ,
,