

 1-3
4-6
7-9
10-12
13-15
16-18
19-21
22-24
25-27
28-30
31-33
34-36
37-39
40-42
43-45
1-3
4-6
7-9
10-12
13-15
16-18
19-21
22-24
25-27
28-30
31-33
34-36
37-39
40-42
43-45




![]() 2
2
![]() >
>![]() 0
0
![]() =
=![]() s
s
![]() λ
λ
![]() 1
1
λ2
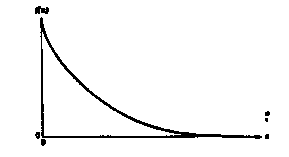
![]() λ
λ![]() - λxe
- λxe![]() ;
;![]() x
x![]() ≥
≥![]() 0
0![]() = 0 elsewhere
= 0 elsewhere

![]() 2
2![]() -
-![]() 1)1
1)1![]() 2
2![]() (eσ
(eσ![]() 2
2![]() +
+![]() 2)
2)

![]() 2μ +
2μ +![]() 2
2
![]() σ
σ![]() (e
(e![]() σ
σ![]() 2
2
![]() 1)
1)

![]() 2
2
![]() μ
μ![]() <
<![]() ∞;
∞;
![]() σ
σ![]() >
>![]() 0
0
![]() (
(![]() x)
x)![]() =
=![]() 1
1![]() σ
σ![]() x
x![]() 2π
2π
![]() ≥
≥![]() 0
0
![]() -
-![]() 1?
1? ![]() 2σ
2σ![]() 2
2
![]() ?
? ![]() (log
(log![]() x
x![]() -
-![]() μ
μ![]() )
)
![]() = 3
= 3![]() + (w - 1)(w
+ (w - 1)(w![]() 3
3![]() + 3w
+ 3w![]() 2
2![]() + 6w + 6);
+ 6w + 6);![]() w = e
w = e![]() σ
σ![]() 2
2
![]() 2
2
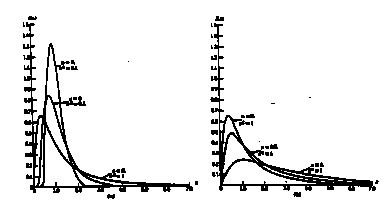
![]() +
+![]() 12
12![]() σ
σ![]() 2
2

![]() μ1
μ1![]() - μ
- μ![]() 0
0![]() )
)![]() 2
2
![]() 12
12

![]() <
<![]() μ
μ![]() 1
1
![]() where
where
1
![]() (
(![]() x)
x)![]() =
=![]() 1?
1?
![]() μ
μ![]() 1
1![]() -
-![]() μ
μ
![]() ?
? ![]() ,
,![]() μ
μ![]() 0
0
![]() 0
0
![]() x
x![]() ≤
≤![]() μ
μ![]() 1
1
![]() 2
2
![]() 0
0![]() +
+![]() μ
μ![]() 1
1
![]() 2
2
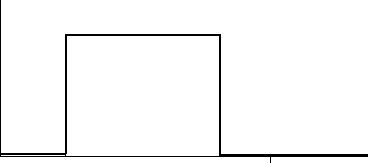
![]() 0
0
![]() 1
1
![]() ,
,![]() μ
μ