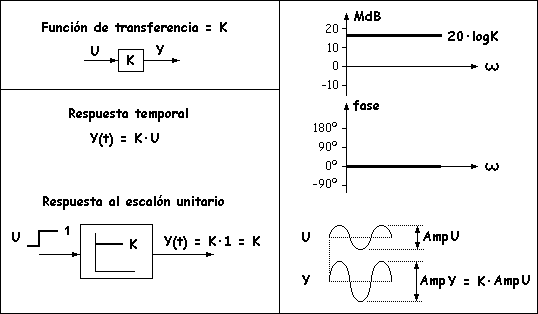
FACTOR PROPORCIONAL.
Un componente tiene un comportamiento proporcional si amplifica o reduce la señal de entrada proporcionalmente, es decir, la salida es igual a la entrada multiplicada por un factor o ganancia K. No está definido por ninguna raíz, ya que solo se trata de un factor que irá multiplicando a otras funciones de transferencia. Al aplicar a su entrada una señal senoidal devuelve otra señal idéntica (excepto en amplitud), independientemente de la frecuencia, por lo que el diagrama del módulo es una recta horizontal. La ganancia (cociente entre amplitud de salida y entrada) coincide con el factor K y el módulo, constante, es igual al logaritmo de K multiplicado por 20. No produce desfase por lo que el diagrama de fase es una recta horizontal que coincide en 0 grados. Es típico analizar la respuesta cuando se aplica en la entrada un escalón unitario, que es una señal que pasa bruscamente de 0 a 1. Como la respuesta es igual a K por la entrada, resulta un valor constante K como respuesta. El símbolo representa la respuesta frente a un escalón unitario y por esta razón es una recta horizontal, como se ha dibujado en la esquina inferior izquierda de la figura.

FACTOR DERIVATIVO.
Son componentes derivativos aquellos que solo reaccionan a los cambios que experimenta la señal de entrada pero transmiten una señal nula cuando la entrada se mantiene constante. Si la entrada es un escalón unitario, su variación es muy brusca en el instante del cambio de 0 a 1 y la respuesta es muy intensa, pero seguidamente la entrada se mantiene constante, por lo que la respuesta se anula. Por esta razón, el símbolo es una recta vertical, que indica un gran aumento en el primer instante y un paso a cero un instante después. Si la entrada no es un escalón, la respuesta coincide, en cada instante, con la pendiente de la gráfica de la señal de entrada. Este concepto se representa matemáticamente con una derivada y así aparece en la figura como respuesta temporal. En la práctica, el valor de una derivada se puede determinar, de forma aproximada, como el cociente entre un pequeño incremento de la señal y el tiempo que tarda en aparecer dicho incremento, siempre y cuando se calcule respecto del tiempo, ya que pudiera ser respecto de otra variable. La aproximación es mejor cuanto menor sea el incremento considerado.

A bajas frecuencias, las variaciones de la entrada son lentas y la respuesta de poca intensidad, pero a frecuencias altas ocurre lo contrario, por lo que se deduce que la amplitud de la oscilación de salida aumenta con la frecuencia, lo mismo ocurrirá con la ganancia (cociente de amplitudes) y el módulo, que, como se vé en la figura, crece a razón de 20 decibelios por década. Se entiende como década el incremento de una unidad en la escala del logaritmo de la frecuencia, nótese que en una década, la frecuencia se multiplica por 10. En la figura se ha marcado un punto que corresponde a un módulo de 40 dB, y, como es lógico, con 2 décadas. En cuanto a la fase, la salida (Y) se adelanta 90º respecto de la entrada (U), ya que cuando la entrada pasa por cero, su pendiente es máxima y también será máxima la salida. La frecuencia a la que aparece un cambio de pendiente en el diagrama del módulo es 0 rad/seg (en la figura es 1 rad/seg por la imposibilidad de ensayar con una frecuencia igual a cero), esto significa que la raíz que representa este tipo de comportamiento está en el origen, es decir, en s = 0. El polinomio o función de transferencia será entonces s - 0 = s.
FACTOR INTEGRAL.
Los componentes que acumulan la señal de entrada son elementos integradores. Si la entrada es un escalón unitario, es claro que el valor acumulado en un tiempo "t" será igual al área del rectángulo que se ha rayado en la figura y como la entrada se mantiene constante (igual a 1), el área será igual a "t". Cuanto mayor sea el tiempo "t", mayor será el valor acumulado y por esa razón se simboliza con una recta ascendente. El valor acumulado con otro tipo de entradas también será igual al área bajo la gráfica de la señal de entrada, pero ya no será un rectángulo. El concepto matemático de un valor acumulado desde un instante 0 hasta un instante "t" es la integral entre los instantes 0 y "t", y así aparece en la figura como respuesta temporal. En la práctica, el valor de una integral puede calcularse, de forma aproximada, estableciendo intervalos de tiempo muy pequeños, y, en cada intervalo, multiplicando el valor de la señal de entrada por el tiempo del intervalo. El resultado del producto se sumará a un valor que servirá como acumulador y que comenzará siendo 0 en el instante inicial. En cualquier instante, el valor que tenga el acumulador será una buena aproximación a la integral.

A bajas frecuencias, la respuesta pasa por valores grandes, porque se acumula señal de entrada durante más tiempo. Al aumentar la frecuencia, el tiempo en que se acumula señal, en cada semiciclo, es menor y por ello también disminuye la amplitud de la salida. Así pues, al aumentar la frecuencia disminuye el módulo, y lo hace a razón de 20 decibelos por década como se vé en la fugura. En cuanto a la fase, se observa que durante cualquier semiciclo positivo de la señal de entrada, la salida estará acumulando valor positivo y crecerá hasta el instante que la entrada llegue a cero, por lo tanto, la salida es máxima cuando la entrada es cero y se deduce que existe un retraso de 90º respecto de la entrada. Como ocurría con el factor derivativo, el cambio de pendiente también aparece con frecuencia cero, y también tiene una raíz en el origen, pero en este caso, la función de transferencia no es "s" sino "1/s" porque su comportamiento es inverso al derivativo. En general, los componentes que producen retraso de fase, como el integral, tienen una función de transferencia con el polinomio en el denominador.
RETARDO DE PRIMER ORDEN.
Es el comportamiento de los componentes que, aunque siguen a la señal de entrada, reaccionan con cierta lentitud, suavizando los cambios bruscos. Si las variaciones son lentas, la salida se aproxima bastante a la entrada, en caso contrario, la salida se distancia. Si la entrada es un escalón unitario, la respuesta crece con suavidad, sin alcanzar nunca el valor 1, pero en la práctica se alcanza los dos tercios en un tiempo igual a la constante de tiempo T (en segundos), que es igual a la inversa de la frecuencia de cruce. En un tiempo 3T se llega al 95% y en 5T al 99%.

Con bajas frecuencias, las variaciones son lentas y apenas existe desfase, a la vez que que se mantiene bastante bien la ganancia. Con altas frecuencias, las variaciones son rápidas y el retraso de fase puede llegar a un máximo de 90º, a la vez que pierde amplitud, por lo que el módulo decrece a razón de 20 db/dec. Como vemos en la figura, existe una frecuencia de cruce que determina un cambio de comportamiento, esta frecuencia coincide con un punto de inflexión en el diagrama de fase, en 45º. Por debajo de la frecuencia de cruce reproduce bastante bien la señal de entrada. Por encima de la frecuencia de cruce se comporta como un filtro que reduce la señal, casi haciéndola desaparecer a elevadas frecuencias. Por esta razón se conocen también como "filtros pasa-bajos", porque dejan pasar bajas frecuencias pero bloquean las altas. La función de transferencia tendrá su polinomio como denominador, ya que el componente produce retraso. Como se desarrolla en la figura, el polinomio se determina a partir de la raíz s1, multiplicando por el factor de conversión correspondiente para que el término independiente sea igual a 1 (normalizado).
RETARDO DE SEGUNDO ORDEN.
Tienen este comportamiento los componentes con capacidad para almacenar energía y devolverla con retraso. La respuesta es similar a la de un retardo de primer orden pero con oscilaciones amortiguadas hasta que alcanza el equilibrio. La amplitud de las oscilaciones es tanto mayor cuanto menor sea su capacidad para consumir energía, es decir, cuanto menor sea su relación de amortiguamiento. Otras diferencias son que el módulo decrece a razón de 40 dB/dec en lugar de 20 y que el retraso máximo de fase llega a los 180º. Las raices que lo identifican con complejas y conjugadas y, como vemos en la figura, dependen de la frecuencia natural de oscilación no amortiguada y de la relación de amortiguamiento. El diagrama del módulo se distancia del trazado asintótico (no concide exactamente con lineas rectas), de modo que la determinación de la frecuencia natural se consigue trazando una tangente al diagrama con pendiente de -40 dB/dec. El punto donde se cortan las asíntotas revela la frecuencia natural y el pico de resonancia (Mr) determina la relación de amortiguamiento mediante la gráfica de la figura.

A continuación se amplía la información acerca de la respuesta al escalón unitario. Dependiendo del valor de la relación de amortiguamiento, la oscilación puede llegar a desaparecer (entre 0.8 y 1) hasta el otro extremo en el que se mantiene (valor 0). Valores negativos hacen que la oscilación aumente en lugar de disminuir.

FACTOR DE PRIMER ORDEN.
Este comportamiento es el inverso del retardo de primer orden. A partir de la frecuencia de cruce aumenta la amplitud de la oscilación en lugar de disminuir, por lo que el módulo crece a razón de 20 dB/dec. Por el mismo motivo existe un adelanto de fase en lugar de un retraso, siendo el adelanto máximo de 90º. Lógicamente, la función de transferencia es también la inversa. La respuesta en función del tiempo será la correspondiente al diagrama de bloques de la esquina inferior izquierda de la figura, que se deduce directamente de la función de transferencia. Por lo tanto, la respuesta es la suma de dos acciones: La primera será igual a la inversa de la frecuencia de cruce por la derivada de la señal de entrada U, ya que "s" es la función de transferencia de un componente derivativo. La segunda es simplemente la señal de entrada porque se trata de un factor proporcional con ganancia igual a 1. La forma de calcular una derivada en la práctica se explicó en el apartado del factor derivativo.

Cuando la raíz de este tipo de factor es positiva en lugar de negativa como se ha representado, no cambia el diagrama del módulo pero sí el de fase, causando un retraso máximo de 90º en lugar de un adelanto.
FACTOR DE SEGUNDO ORDEN.
Este comportamiento es el inverso del retardo de segundo orden. Como se ve en la figura, la función de transferencia es la inversa, a partir de la frecuencia natural crece el módulo a razón de 40 dB/dec en lugar de disminuir, la fase adelanta un máximo de 180º en lugar de retrasar. Por último, la respuesta en función del tiempo se deduce del diagrama de bloques, que se ha dibujado en la esquina inferior izquierda de la figura. En este caso, la primera rama contiene dos factores derivativos en serie, que equivale a la segunda derivada de la señal de entrada U respecto del tiempo. Una segunda derivada se calcula, simplemente, derivando dos veces, es decir, calculando la derivada de U y calculando de nuevo la derivada con el resultado de la primera derivada.

TIEMPO MUERTO O RETARDO DE TRANSPORTE.
Con este comportamiento, la salida transmite los mismos valores que va tomando la entrada pero con un retraso de tiempo igual a Tau, según figura. Si la entrada es un escalón unitario, la salida también lo será, sin el redondeo o suavizado que caracteriza a los retardos de primer orden. La amplitud de la señal de salida será la misma que la de la entrada, por lo que la ganancia será igual a 1 y el módulo igual a 0, independientemente de la frecuencia. En cuanto a la fase, se produce un retraso que aumenta indefinidamente al aumentar la frecuencia. La respuesta en función del tiempo es la misma que tuviera la señal de entrada un determinado tiempo antes, como si el componente retuviera la señal y la fuera devolviendo un tiempo más tarde. No será necesario este tipo de comportamiento para implementar un regulador porque siempre es perjudicial. También es perjudicial en el sistema a regular, porque siempre lo acerca a la inestabilidad, por lo tanto, es aconsejable eliminarlo en el mayor grado que sea posible. Por ejemplo, en un sistema con transmisión de calor será importante que el sensor esté lo más cerca posible del foco de calor, para reducir el tiempo que tarda el calor en propagarse hasta llegar al sensor. Generalmente, no se utiliza ningún componente con este comportamiento, pero existe en mayor o menor grado en todos los sistemas. Si nos fijamos en la función de transferencia, solo se anula si "s" se hace infinito, es por lo tanto equivalente a una raíz en el infinito
