

A base de prueba y error existen sistemas fáciles de regular, difíciles e imposibles. Pero en todos ellos, una regulación incorrecta los puede hacer oscilar, como lo haría un peso colgado de un muelle cuando se saca del reposo con un impulso inicial. Si el sistema tiene una reducida capacidad para consumir energía, la oscilación se mantiene largo tiempo hasta su desaparición. Si existe un medio que consume mucha energía, la oscilación desaparece rápidamente, tal como sucedería si el peso se sumerge en un líquido viscoso como representa la figura. Cuando se aplica una energía pulsatoria con frecuencia variable, se obserba que a determinada frecuencia se incrementa la oscilación. En esas condiciones, si el sistema consume menos energía que la que recibe, la oscilación crece indefinidamente en amplitud y, dependiendo del sistema, puede llegar a destruirse. Es conocido el caso del puente de Tacoma Narrows (Washington), que recibió el sobrenombre de puente galopante porque bastaba con un viento moderado para hacerlo oscilar, hasta el punto de terminar destruido. Desde entonces, los puentes se diseñaron para hacerlos aerodinámicamente estables.
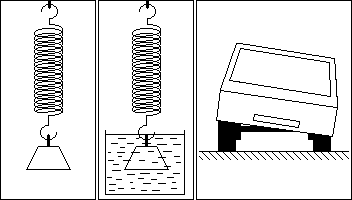
El sencillo sistema que acaba de ser descrito se aplica en la suspensión de los automóviles: El peso es el del propio vehículo y en cada rueda existe un muelle y un amortiguador, siendo el amortiguador el encargado de consumir energía por el rozamiento de un émbolo en el interior de un fluido. Aunque un amortiguador mejora el comportamiento, los vehículos modernos ya no se comportan en las curvas como se ha dibujado en la figura. La razón es que se añade una regulación de la inclinación que mejora el comportamiento natural del sistema, a la vez que se mantiene su capacidad para absorber las ondulaciones de la carretera.
El fenómeno por el que un sistema amplifica sus oscilaciones a una determinada frecuencia se conoce como RESONANCIA y la frecuencia a la que sucede se denomina frecuencia natural de oscilación no amortiguada o simplemente, frecuencia de resonancia (en realidad la frecuencia de resonancia es ligeramente menor que la frecuencia natural). El fenómeno de resonancia es la razón por la que un receptor de radio o de televisión sintoniza los diferentes canales o emisoras. Durante la búsqueda de un canal varía la frecuencia de oscilación de un circuito, y cuando coincide con la frecuencia de una emisora entra en resonancia y se amplifican las oscilaciones que la emisora transmite en forma de ondas electromagnéticas, con la información necesaria para reproducir imágenes o sonido. En un receptor se busca expresamente el fenómeno de resonancia y los circuitos osciladores de las emisoras deben oscilar permanentemente. Al contrario, no tratándose de osciladores, los sistemas de regulación deben eliminar o reducir en gran medida los fenómenos de resonancia.
INFORMACIÓN CONTENIDA EN UNA FUNCIÓN DE TRANSFERENCIA.
La regulación de un sistema en lazo cerrado, tan relacionada con las frecuencias y los fenómenos de resonancia, puede conseguirse si las funciones de transferencia registran las siguientes informaciones: Su estabilidad, su frecuencia de resonancia y su grado o relación de amortiguamiento.
Para una determinada frecuencia natural de oscilación no amortiguada, la relación de amotiguamiento puede ser mayor o menor. Esto puede representarse en un sistema de ejes (sigma y omega) mediante un punto "s" cuya distancia al origen se corresponda con la frecuencia natural y su proyección horizontal (sobre el eje sigma) con el amortiguamiento. El coseno del ángulo beta representa entonces su relación de amortiguamiento. La proyección sobre el eje vertical (omega) se puede interpretar como la frecuencia natural amortiguada. Las coordenadas del punto, expresadas en función de la frecuencia natural y la relación de amortiguamiento, aparecen recuadradas en la figura:
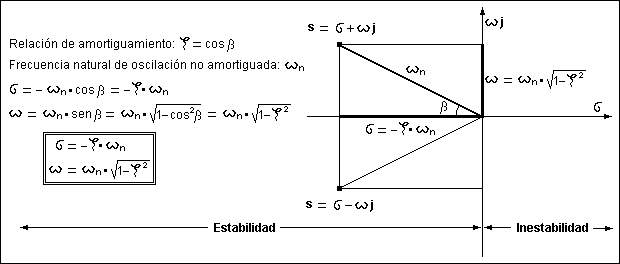
Una relación de amortiguamiento igual a 1 (beta igual a 0 grados) implica el mayor amortiguamiento posible, lo que identificará un componente que no puede oscilar y que por lo tanto será estable. Una relación de amortiguamiento entre 1 y 0 (beta entre 0º y 90º) identificará un componente con capacidad de oscilar de forma amortiguada, de modo que sigue siendo estable porque mantiene una determinada capacidad de amortiguar las oscilaciones. Una relación de amortiguamiento menor o igual que 0 (beta mayor o igual de 90º) identificará un componente inestable. Así pues, las zonas de estabilidad e inestabilidad quedan definidas a un lado y otro del eje vertical.
La representación gráfica que se ha planteado, aunque contiene la información necesaria, debe ser convertida en una expresión que pueda ser sumada, restada y multiplicada, sin que se pierda la información individual de cada componente, tal como ha sido definido en el apartado anterior. La solución al problema casi salta a la vista: Cada punto bien puede ser la raíz de un polinomio, es decir, un valor de la variable que hace al polinomio igual a cero. Como las raices pueden ser reales o complejas, también representan puntos en un sistema de dos ejes, uno real (sigma) y otro imaginario (omega), siendo "j" la unidad imaginaria, que es igual a la raíz cuadrada de -1. Las raices imaginarias siempre aparecen por parejas y son conjugadas, razón por la que se han representado dos puntos simétricos respecto del eje sigma en la figura anterior.
Siendo s1 y s2 dos raices complejas y conjugadas como las de la figura anterior, el polinomio se obtiene como el producto (s - s1)·(s - s2), ya que se hace cero cuando s es igual a cualquiera de las dos raices. Sustituyendo sigma y omega en s1 y s2 por las expresiones recuadradas en la figura anterior y desarrollando, resulta un polinomio de segundo orden como el recuadrado a continuación, en el que ha desaperecido la unidad imaginaria "j = raiz cuadrada de -1", ya que en el término que está elevado al cuadrado se convierte en -1 y en los demás términos se simplifica.

Es conveniente que el término independiente de los polinomios sea igual a 1 (se verá porqué más adelante), de modo que aparece un factor de conversión, que aplicado a (s - s1)·(s - s2) permite llegar directamente al polinomio en su expresión "normalizada". La siguiente figura trata el caso de una sola raíz en el eje real. En este caso no existe fenómeno de resonancia y la distancia del punto al origen no se llamará frecuencia natural sino frecuencia de cruce. Para obtener el polinomio "normalizado" se aplica igualmente el factor de conversión recuadrado en la figura.

Además de los dos tipos de polinomios descritos existe también el caso particular de una raíz en el origen y una raíz en +infinito. Con una raíz en el origen, el polinomio es simplemente igual a "s", sin término independiente y por lo tanto sin factor de conversión. Con una raíz en +infinito es un caso especial que corresponde a un tiempo muerto o retardo de transporte. Por último, también existe el inverso de cada uno de los casos, excepto del tiempo muerto. Para el estudio particular de cada caso nos basaremos en el diagrama de Bode, que es un método experimental para determinar funciones de transferencia y sirve indistintamente para componentes individuales de un sistema o para el sistema completo. El diagrama de Bode, que veremos en el siguiente apartado, aportará información muy significativa sobre cada uno de los casos de funciones de transferencia mencionados en este apartado.