ARBOLES

INTRODUCCIÓN:

Al analizar la estructura árbol se introduce un concepto, que es el de estructura de ramificación entre nodos.
Estos árboles representan las estructuras no-lineales y dinámicas de datos mas importante en computación.
Dinámicas, puesto que la estructura árbol puede cambiar durante la ejecución del programa.
No-lineales, debido a que cada elemento puede seguirle varios elementos.

DEFINICIÓN

Un árbol es una estructura jerárquica sobre una colección de datos u objetos llamados nodos, uno de los cuales es conocido como raíz. Además se crea una relación o parentesco entre los nodos dando lugar a terminos como padre, hijo, hermano, antecesor, sucesor, entre otros.

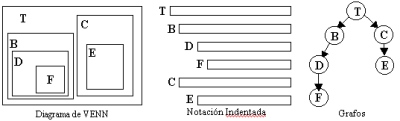
REPRESENTACIÓN

Formalmente se define un árbol de tipo T como una estructura homogénea que puede ser:

PROPIEDADES Y CARACTERÍSTICAS
§ Todo árbol que no es vacío, tiene un único nodo raíz.
§ X es hijo de Y, si X es apuntado por Y.
§ X es padre de Y, si el nodo X apunta a Y.
§ Son hermanos si son descendientes de un mismo nodo.
§ Terminal u hoja, si el nodo no tiene ramificaciones.
§ Nodo interior, si no es nodo raíz, ni terminal u hoja.
§ Grado, es el número de descendientes de un determinado nodo.
§ Grado de un árbol, es el máximo grado de todos los nodos del árbol.
§ Nivel, es el número de arcos que deban ser recorridos para llegar a un nodo.[Por definición el nodo raíz tiene nivel 1].
§ Altura, es el máximo número de niveles de todos los nodos del árbol.

Longitud de Camino Interno.-

Longitud de Camino Externo.-
Árbol extendido: Es aquel en el que el número de hijos de cada nodo es igual al grado del árbol.
Nodo especial: Este tipo de nodos no puede tener descendientes y normalmente se representa con la forma de un cuadrito, que vienen a reemplazar las ramas vacías o nulas.

TIPOS DE ÁRBOLES

Árboles Binarios (AB):
Son considerados árboles de grado 2, son de especial interés ya que representan una de las estructuras de datos más importantes en computación.
Esto significa que en cada nodo puede tener como máximo dos subárboles, y siempre es necesario distinguir entre el subárbol izquierdo y el derecho.
Este tipo de árboles tienen múltiples aplicaciones, desde una construcción historica de un campeonato, pasando por la evaluación de expresiones algebraicas con operadores binarios, hasta la representación de una estructura en la cual es posible la toma de decisiones con dos opciones en distintos puntos de un proceso.
AB Distintos, cuando sus estructuras son diferentes.
AB Similares, cuando sus estructuras son idénticas y su información diferente.
AB Equivalentes, cuando son similares y los nodos contienen la misma información.
AB Completos, si todos los nodos excepto los del último nivel, tienen dos hijos. En estos árboles se pueden calcular Nro de hijos = 2h-1.

Su representación en Memoria:

Su recorrido:
Preorden Inorden Postorden
Recorrer subárbol izq.Recorrer raíz.Recorrer subárbol der. Recorrer raíz.Recorrer subárbol izq.Recorrer subárbol der. Recorrer subárbol izq.Recorrer subárbol der.Recorrer raíz.

Árboles Balanceados:
Estos surgen al crecimiento descontrolado en AB, y será N/2.
Para todo nodo del árbol T, la altura de los subárboles IZQ y DER no deben diferir en más de una unidad.

Árboles Multicaminos:
Es la variante de los AB, puesto que muchas aplicaciones en las que el volumen de información es tal, que estos no caben en memoria principal y es necesario almacenarlos y organizarlos en archivos, en dispositivos de almacenamiento secundario. La misma debe ser suficientemente adecuada para recuperar los datos de forma eficiente. Es por esta razón que su primera implementación fue en ÁRBOLES B y luego se mejoro con ÁRBOLES B+.
ÁRBOLES B, este tipo de estructura los nodos terminal u hoja están en el mismo nivel.

ÁRBOLES B+, este tipo de árboles se han convertido en la técnica más utilizada para la organización de archivos indizados. La principal característica de estos, es que todas las claves o datos se encuentran en las hojas por lo tanto cualquier camino desde la raíz hasta alguna clave tienen la misma longitud.
Formalmente se define este árbol así:

§ Cada página, excepto la raíz, contiene entre d y 2d elementos.
§ Cada página, excepto la raíz, tiene entre d+1 y 2d+1 descendientes.
§ La página tiene al menos 2 descendientes.
§ Las páginas hoja están todas al mismo nivel.
§ Todas las claves se encuentran en las páginas hoja.
§ Las claves de las páginas raíz e interiores se utilizan como índices.

Descargue en