

Educational Goal: Students will learn how to determine the values of sines and cosines of angles different than 30°, 45° and 60° associating these angles with others in different quadrants of the trigonometric circle.
Behavioral Objective: Students will be able to establish the relationship between the trigonometric ratios on the right angle triangle and the trigonometric circle.
Materials: Student notebooks, worksheets, ruler, a pair of squares, chalkboard and chalk.
Time Required: 100 to 120 minutes.
Background: Students should already know the following definitions:


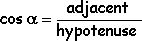
They also have to know the coordinators of a point in the Cartesian Plan. So, when start saying that there is a circle with center on the origin and ratio equals to one, they have to be able to identify the four intersections between the circle and the axes, i.e., the points: (1, 0), (0, 1), (-1, 0) and (0, -1).
Introduction: Write on the chalkboard the following table:
30°
45°
60°
sin
cos
Ask for a volunteer to come up and complete the table.
After that, add three more columns to the table and ask if one can complete the table now:
30°
45°
60°
120°
135°
150°
sin
cos
Explain that they can find out these values without a calculator since they discover how to associate the new angles to the previous ones.
| Development: |
 Go on
Go on
|