Gerwin Griffioen's Technical Analysis Pages
Griffioen, G.A.W. (2003), "Technical Analysis in Financial Markets", PhD thesis, University of Amsterdam.
Chapter 2
Success and Failure of Technical Trading Strategies in the Cocoa Futures Market
2.1 Introduction
This chapter is an attempt to answer questions raised by a financial practitioner, Guido Veenstra, employed at the leading Dutch cocoa-trading firm, Unicom International B.V. at Zaandam. Unicom is part of a bigger consortium that buys crops of cocoa at the Ivory Coast, where it has a plant to make some first refinements of the raw cocoa. The cocoa beans are shipped to Europe where they are transformed to cocoa-butter, cocoa-powder and cocoa-mass in plants in France and Spain. These raw cocoa products serve as production factors in the chocolate industry. The first goal of Unicom is to sell the raw cocoa beans as well as the raw cocoa products to chocolate manufacturers. A second important task of Unicom is to control the financial risks of the whole consortium. The consortium faces currency risk as well as cocoa price risk. Unicom monitors the product streams and uses cocoa futures contracts, mainly those traded at the London International Financial Futures Exchange (LIFFE), to hedge the price risk. Unicom trades cocoa futures through brokers. However, the commission fees give the brokers an incentive to contact their clients frequently and to give them sometimes unwanted advice to trade as much as possible. Brokers' advices are partly based on technical analysis.In addition to cocoa producers, more and more speculators seem to be trading on the cocoa futures markets who use technical analysis as a forecasting tool. If a lot of speculators with a large amount of money are trading in a market, they may affect realized futures prices through their behavior. The question ``Can cocoa futures prices be predicted by technical analysis?'' thus becomes important from a practitioner's viewpoint. This question is not only important to cocoa producers, but in general to producers of any commodity hedging price risk. If technical analysis has forecasting power and speculators take positions in the market on the basis of technical analysis, these speculators can affect market prices. Why should a (cocoa) producer go short in the futures market to hedge his price risk exposure if he knows that a lot of speculators in the market are buying long positions driving up the price? Knowledge of the behavior of speculators in the market may be useful to adapt a producers' price hedging strategy.
Until fairly recently, the academic literature has paid little attention to technical trading strategies. Until the 1980s the efficient markets hypothesis (EMH) was the dominating paradigm in finance, see e.g. Fama (1970) and Samuelson (1965). According to a strong form of the EMH, financial time series follow a random walk and are thus inherently unpredictable. All information is discounted in the prices already and prices will only adapt if new information becomes available. Because news arrives randomly, prices will move randomly. According to the EMH, financial time series are unpredictable and technical analysis is useless and cannot lead to statistically significant prediction or economically significant profits.
In the last decade however, technical analysis has regained the interest of many economic researchers. Several authors have shown that financial prices and returns are forecastable to some extent, either from their own past or from some other publicly available information, see e.g. Fama and French (1988), Lo and MacKinlay (1988, 1997, 1999) and Pesaran and Timmermann (1995, 2000). In particular, it has been shown that simple technical trading rules used in financial practice can generate positive profits and can have statistically significant forecasting power. For example Brock, Lakonishok and LeBaron (1992) test 26 simple technical trading rules on daily data of the Dow-Jones Industrial Average (DJIA) in the period 1897-1986. Each of the trading rules Brock et al. (1992) test generates higher returns during buy days, that is periods following buy signals, than during sell days, that is periods following sell signals. Further they find that returns following buy signals are less volatile than returns following sell signals. By applying bootstrap techniques they show that their results are not consistent with some popular null models like the random walk, the AR(1), the GARCH-in-mean and the exponential GARCH model. LeBaron (2000) performs the same analysis as Brock et al. (1992) for the period 1988-1999 and finds that trading rules perform much worse in this period, but that volatility remains different between buy and sell periods. Levich and Thomas (1993) test filter and moving-average trading rules on foreign currency futures prices in the period 1976-1990. Applying bootstrap techniques they conclude that the profits of the technical trading strategies cannot be explained by a random walk model or by autocorrelation in the data. LeBaron (1993) applies trading rules to exchange rates based on interest rate differentials, moving averages and volatility comparison and concludes that the trading rules tested have forecasting power.
Several authors have emphasized the danger of data snooping, meaning that if one searches long enough in a data set, there will always appear one trading strategy that seems to work. Many authors mitigate this problem by using only trading rules that are frequently used in financial practice or by reporting the robustness of their results across different subperiods. However, Sullivan, Timmermann and White (1999) noted that such trading strategies could be the result of survivorship bias, since the currently used trading rules in practice can be the result of a continuous search for the best strategy. Therefore they propose to use White's (2000) Reality Check bootstrap methodology to correct for data snooping. Sullivan et al. (1999) take the results of Brock et al. (1992) on the DJIA in the period 1897-1986 as starting point. They find that the results of Brock et al. (1992) are robust to data snooping in the period 1897-1986, but that in the period 1987-1997 the performance of the best trading rule is not significant when corrected for data snooping. Sullivan et al. (1999) show that the same results hold for a universe of 7846 trading rules and conclude that the worse performance of trading rules in the period 1987-1997 may be explained by a change of the market mechanism, e.g. an increase of market efficiency due to lower transaction costs and increased liquidity.
The present chapter is empirical and tests the profitability and predictability of objective trend-following technical trading techniques in the cocoa futures markets in the period 1983:1-1997:6. In order to avoid the problem of data snooping our approach is to test a large set of more than 5000 trading strategies, moving average, trading range break-out and filter rules, and to investigate the magnitude of the fraction generating strictly positive excess returns and statistically significant forecasting power. Cocoa futures contracts are traded at two different exchanges, namely at the Coffee, Sugar and Cocoa Exchange (CSCE) in New York and the London International Financial Futures Exchange (LIFFE). The results for the two cocoa futures contracts are strikingly different. When applied to the LIFFE cocoa futures prices, 58.3% of all trading rules generate strictly positive excess returns, even when correcting for transaction costs. Furthermore, a large set of trading rules exhibits statistically significant forecasting power of the LIFFE cocoa futures series, with e.g. 26.6% having significantly positive mean buy minus sell return; for the 5 year subperiod 1983:1-1987:12 even 46.7% of all trading rules has a significantly positive mean buy minus sell return. However, the same set of strategies performs poorly on the CSCE cocoa futures prices, with only 12.2% generating positive net excess returns and hardly any statistically significant forecasting power. The large difference in the performance of technical trading is surprising, because the underlying asset in both markets is more or less the same. Our findings may be attributed to a combination of the demand/supply mechanism in the cocoa market and an accidental influence of the Pound-Dollar exchange rate. Due to a spurious relation between the level of the Pound-Dollar exchange rate and the excess demand/supply mechanism in the cocoa market, especially in the period 1983:1-1987:12, trends caused by the demand/supply mechanism were reinforced in the LIFFE cocoa futures price, but the same trends were weakened in the CSCE cocoa futures price. Many technical trading rules are able to pick up these sufficiently strong trends in the LIFFE cocoa futures but almost none of them pick up the weaker trends in the CSCE cocoa futures.
The chapter is organized as follows. In section 2.2 we describe our data set and the construction of a long, continuous time series of 15 years out of 160 different (overlapping) futures contracts of 18 months. Section 2.3 gives an overview of the 5350 trading rules we apply; the parameterizations of these rules can be found in Appendix B. In section 2.4 the performance measure, i.e. the excess return net of transaction costs generated by the trading rules, is calculated. Section 2.5 focuses on the economic performance as well as the statistical significance of the predictability of returns by technical trading rules. The statistical tests are performed first under the assumption of iid returns but later also by correcting for dependence in the data. This is done by estimating exponential GARCH models with a dummy for the trading position in the regression equation, but also by applying bootstrap techniques, the results of which are presented in section 2.6. In section 2.7 a possible explanation of the large differences in the performance between CSCE and the LIFFE cocoa futures prices is given. Finally, section 2.8 concludes.
2.2 Data
2.2.1 Data series
A commodity futures contract is an agreement between two parties to trade a certain asset at some future date. The contract specifies the quality and quantity of the good as well as the time and place of delivery. The price against which the contract is traded is called the futures price. The expiry months of cocoa futures contracts are March, May, July, September and December. Each contract asks for the delivery of ten tons of cocoa. The LIFFE contract specifies that at each trading day ten expiry months are available for trading. The CSCE and LIFFE cocoa futures contracts differ somewhat in their specifications. First, cocoa is grown in many regions in Africa, Asia and Latin America and therefore the crops differ in quality. In the futures contracts a benchmark is specified and the other crops are traded at premiums. The benchmark in the LIFFE contract has a higher quality than the benchmark in the CSCE contract. Therefore the benchmark in the LIFFE contract is traded at a $160/ton1 premium in the CSCE contract. Second, the place of delivery in the CSCE contract is near New York, while the places of delivery in the LIFFE contract are nominated warehouses at different places in Europe. Third, the tick sizes of the CSCE and LIFFE contract are respectively one Dollar and one Pound. Cocoa producers and farmers hedge their price risk exposure with futures contracts. This guarantees them that they buy or sell cocoa against a predetermined price. The futures price will depend on the current and expected future demand and supply. When new information becomes available the price will adapt. Normally a futures price is the derivative of the spot price and can be computed by the cost of carry relationship. But in the case of soft commodities such as cocoa the spot price is not relevant, because a farmer with his crop on the land only wants to know what he can get in the future. For cocoa there is no actual spot price, but the ``notional'' spot price is in fact determined by the futures prices.We investigate data on the settlement prices of 160 cocoa futures contracts that expire in the period January 1982 through December 1997 at the CSCE and the LIFFE2, as well as data on the Pound-Dollar exchange rate (WM/Reuters) and 1-month UK and US certificates of deposit (COD) interest rates in the same period.
2.2.2 A continuous time series of futures prices
Each futures contract covers a limited time span of approximately 18 months. Thus there is no continuous time series of futures prices over a couple of years. In this section we describe how a continuous time series can be constructed out of the prices of the separate contracts. The well-known formula of the price of a futures contract at day t which expires at day T is Here St is the spot price of the underlying asset at time t, and rtf, ut, yt are respectively the daily risk-free interest rate, storage costs and convenience yield averaged over the period (t,T] at time t with continuous compounding. The convenience yield can be described as the utility of having the asset in stock. The term (rtf+ut-yt) is called the cost of carry and (2.1) is called the cost of carry relationship. The daily return rtF of the futures contract, expressed as the log difference, is given by This formula shows that a change in one of the factors of the cost of carry has an impact on the futures price. Otherwise, the return of a futures contract is equal to the excess return of the underlying asset over the cost of carry.Assume that we have two futures contracts, 1 and 2, with futures prices Ft(1) and Ft(2) and expiry dates T2 > T1. It follows from (2.2) that two futures contracts traded in the same period have the same trends in prices. The futures price of contract 2 can be expressed in terms of the futures price of contract 1 as Notice that rtf, ut and yt are numbers averaged over (t,T]. Thus in equation (2.3) it is assumed that rtf, ut and yt averaged over (t,T1] is equal to rtf, ut and yt averaged over (t,T2]. Formula (2.3) shows that if, as is usual, the cost of carry is positive, the futures price of contract 2 which expires later is higher than the futures price of contract 1 which expires earlier. But if the utility of having an asset in stock is high, e.g. when there is a shortage of the commodity in the short run, then the futures price of contract 2 can be lower than the futures price of contract 1. Thus the prices of different futures contracts can move at different price levels.
A long continuous time series of futures prices will be constructed, in order to be able to test technical trading strategies with long memory. The continuous time series must be constructed out of the many price series of the different futures contracts that have the same price trends, but move at different price levels. In particular roll over dates must be defined at which the price movements of the different contracts are pasted together. In practice most trading occurs in the second nearest contract, that is the futures contract that has the one but nearest expiration date. We investigated the liquidity of the cocoa futures contracts and decided to take as roll over dates the date one month before most of the practitioners switch to the next contract, so that the continuous time series always represents a high liquidity futures contract. Figure 2.1 exhibits graphically the roll over procedure used in this chapter.
The holder of the long position in a futures contract pays a time premium to the holder of the short position. According to (2.1) the time premium paid at time t is According to (2.4) the time premium that must be paid will be less when the duration of the contract is shorter other things being equal. However, (2.4) also implies that if a continuous time series of futures prices is constructed by pasting the prices of different contracts, at each pasting date3 a new time premium to the time series is added, because at each pasting date the time until expiration will be longer than before the pasting date. This time premium will create price jumps and therefore an upward force in the global price development. In fact, if the return of the underlying asset is not greater than the cost of carry a spurious upward trend can be observed in the continuous price series, as illustrated in figure 2.2, which may affect the performance of long memory trading strategies. Therefore we constructed a continuous time series of futures prices by pasting the returns of each futures contract at the roll over dates and choosing an appropriate starting value; see figure 2.2. For this continuous series, discontinuous price jumps and spurious trends will disappear and the trends will show the real profitability of trading positions in futures contracts.
2.2.3 Summary statistics
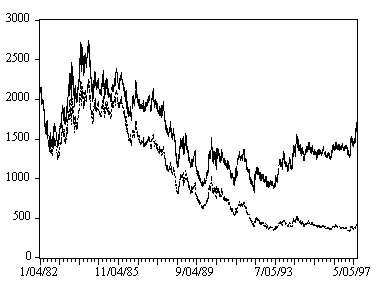
In figure 2.3 time series are shown of the continuation of the CSCE and LIFFE cocoa futures prices and returns as well as the Pound-Dollar exchange rates and returns for the period 1982:1-1997:6. The long-term and short-term trends can be seen clearly. Each technical trading strategy needs a different time horizon of past prices to generate its first signal. Therefore the first 260 observations in each data set will be used to initialize the trading rules, so that on January 3, 1983 each rule advises some position in the market. All trading rules will be compared from this date. Table 2.1 shows the summary statistics of the daily returns of the sample 1983:1-1997:6 and three subperiods of five years. Returns are calculated as the natural log differences of the level of the data series.Table 2.2 shows the estimated autocorrelation functions, up to order 20, for all data series over all periods. Typically autocorrelations are small with only few lags being significant.5 The CSCE series shows little autocorrelation. Only for the first subperiod the second order autocorrelation is significant at a 5% significance level. The LIFFE series shows some signs of low order autocorrelation, significant at the 10% level, in the first two subperiods. The Pound-Dollar series has a significant first order autocorrelation at a 1% significance level, mainly in the first two subperiods.
2.3 Technical trading strategies
Murphy (1986) defines technical analysis as the study of past price movements with the goal to forecast future price movements, perhaps with the aid of certain quantitative summary measures of past prices such as ``momentum'' indicators (``oscillators''), but without regard to any underlying economic, or ``fundamental'' analysis. Another description is given by Pring (1998) who defines technical analysis as the ``art'' of detecting a price trend in an early stage and maintaining a market position until there is enough weight of evidence that the trend has reversed.There are three principles underlying technical analysis. The first is that all information is gradually discounted in the prices. Through the market mechanism the expectations, hopes, dreams and believes of all investors are reflected in the prices. A technical analyst argues that the best adviser you can get is the market itself and there is no need to explore fundamental information. Second, technical analysis assumes that prices move in upward, downward or sideways trends. Therefore most technical trading techniques are trend-following instruments. The third assumption is that history repeats itself. Under equal conditions investors will react the same leading to price patterns which can be recognized in the data. Technical analysts claim that if a pattern is detected in an early stage, profitable trades can be made.
In this thesis we confine ourselves to objective trend-following technical trading techniques which can be implemented on a computer. In this chapter we test in total 5350 technical trading strategies divided in three different groups: moving-average rules (in total 2760), trading range break-out (also called support-and-resistance) rules (in total 1990) and filter rules (in total 600). These strategies are also described by Brock, Lakonishok and LeBaron (1992), Levich and Thomas (1993) and Sullivan, Timmermann and White (1999). Lo, Mamaysky and Wang (2000) use non-parametric methods to implement other, geometrically based technical trading rules such as head-and-shoulder pattern formation. We use the parameterizations of Sullivan et al. (1999) as a starting point to construct our sets of trading rules. These parameterizations are presented in Appendix B. The strategies will be computed on the continuous cocoa time series and the Pound-Dollar exchange rate. If a buy (sell) signal is generated at the end of day t, we assume that a long (short) position is taken in the market at day t against the settlement price of day t.
2.3.1 The moving-average trading rule
Moving-average (MA) trading rules are the most commonly used and most commonly tested technical trading strategies. Moving averages are recursively updated averages of past prices. They yield insight in the underlying trend of a price series and also smooth out an otherwise volatile series. In this thesis we use equally weighted moving averages| MAtn= |
|
|
Pt-j, |
MA trading rules make use of one or two moving averages. A special case is the single crossover MA trading rule using the price series itself and a MA of the price series. If the price crosses the MA upward (downward) this is considered as a buy (sell) signal. The double crossover MA trading rule on the other hand uses two moving averages, a slow one and a fast one. The slow MA represents the long run trend and the fast MA represents the short run trend. If the fast MA crosses the slow MA upward (downward) a buy (sell) signal is given. The signal generating model is given by6
|
We call the single and double crossover MA rules described above, the basic MA trading rules. These basic MA rules can be extended with a %-band filter, a time delay filter, a fixed holding period and a stop-loss. The %-band filter and time delay filter are developed to reduce the number of false signals. In the case of the %-band filter, a band is introduced around the slow MA. If the price or fast MA crosses the slow MA with an amount greater than the band, a signal is generated; otherwise the position in the market is maintained. This strategy will not generate trading signals as long as the fast MA is within the band around the slow MA. The extended MA model with a b · 100% filter is given by
|
2.3.2 Trading range break-out
Our second group of trading rules consists of trading range break-out (TRB) strategies, also called support-and-resistance strategies. The TRB strategy uses support and resistance levels. If during a certain period of time the price does not fall below (rise beyond) a certain price level, this price level is called a support (resistance) level. According to technical analysts, there is a ``battle between buyers and sellers'' at these price levels. The market buys at the support level after a price decline and sells at the resistance level after a price rise. If the price breaks through the support (resistance) level, an important technical trading signal is generated. The sellers (buyers) have won the ``battle''. At the support (resistance) level the market has become a net seller (buyer). This indicates that the market will move to a subsequent lower (higher) level. The support (resistance) level will change into a resistance (support) level. To implement the TRB strategy, support-and-resistance levels are defined as local minima and maxima of the closing prices. If the price falls (rises) through the local minimum (maximum) a sell (buy) signal is generated and a short (long) position is taken in the market. If the price moves between the local minimum and maximum the position in the market is maintained until there is a new breakthrough. The TRB strategy will also be extended with a %-band filter, a time delay filter, a fixed holding period and a stop-loss. The basic TRB strategy, extended with a %-band filter, is described by
|
2.3.3 Filter rule
The final group of trading strategies we test is the group of filter rules, introduced by Alexander (1961). These strategies generate buy (sell) signals if the price rises (falls) by x% from a previous low (high). We implement the filter rule by using a so called moving stop-loss. In an upward trend the stop-loss is placed below the price series. If the price goes up, the stop-loss will go up. If the price declines, the stop-loss will not be changed. If the price falls through the stop-loss, a sell signal is generated and the stop-loss will be placed above the price series. If the price declines, the stop-loss will decline. If the price rises, the stop-loss is not changed. If the price rises through the stop-loss a buy signal is generated and the stop-loss is placed below the price series. The stop-loss will follow the price series at a x% distance. On a buy (sell) signal a long (short) position is maintained. This strategy will be extended with a time delay filter and a fixed holding period. In total our group of filter rules consists of 600 trading strategies.As can be seen in Appendix B we can construct a total of 5350 trading strategies (2760 MA-rules, 1990 TRB-rules, and 600 Filter-rules) with a limited number of values for each parameter. Each trading strategy divides the data set of prices in three subsets. A buy (sell) period is defined as the period after a buy (sell) signal up to the next trading signal. A neutral period is defined as the period after a neutral signal up to the next buy or sell signal. The subsets consisting of buy, sell or neutral periods will be called the set of buy, sell or neutral days.
2.4 Performance measure
2.4.1 Cocoa futures prices
Suppose Pt is the level of the continuous futures price series at the end of day t and Post is the position held in the market by the trader at day t. When trading a futures contract, it is required to hold some margin on a margin account to protect the broker against defaults of the traders. Profits and losses are directly added and subtracted from the margin. A risk-free interest rate can be earned on the margin account. Suppose a trader takes a long or short position in the market against the settlement price at day t-1, Pt-1, and assume that he deposits Pt-1 on his margin account. In this case the broker is fully protected against defaulting7. Then the margin of the trader at the end of day t is equal toMt=(1+rtf)Mt-1+(Pt-Pt-1) Post,
where Mt-1=Pt-1, if as in the case described above the position is held for the first day, otherwise Mt-1 is just the margin build up until time t-1. Further, rtf is the daily risk-free interest rate. The profit or loss of the trader on the futures position in period t directly added to or subtracted from the margin account is equal to (Pt-Pt-1) Post.We will also consider transaction costs. Costs are calculated as a fraction c of the price. Some strategies generate trading signals very often, others not. If a strategy does not generate trading signals very often and a position in the market is maintained for a long time, then there are also trading costs due to the limited life span of a futures contract. In particular, we assume that if a certain position in the market is maintained for 20 days after a roll over date, a trade takes place since the position has to be rolled over to the next futures contract and transaction costs must be paid. This approach leads to a fair comparison of the cost structure of strategies that generate many signals with strategies that generate only a few signals.
Finally, the gross return on time t is calculated as
If no position is held in the market, i.e. Post=0, then according to the formula above a risk-free interest rate is earned. Formula (2.5) represents in the best way the daily return generated by a long as well as a short position in a futures contract. The net return with continuous compounding can be computed by taking the natural logarithm of (2.5). The excess return over the risk-free interest rate and after correcting for transaction costs of trading futures contracts we compute as rte=ln(1+rt)-ln(1+rtf). If we take the cumulative excess return, åt=1T rte, to the power e, then we get
Equation (2.6) determines how much better a technical trading strategy performs relatively to a continuous risk free investment. Hence (A-1)*100% determines how much percent the strategy performs better than a risk free investment.
We take as a proxy for the risk-free interest rates the 1-month US and UK certificates of deposits (COD), which we recompute to daily interest rates. Costs of trading c are set equal to 0.1% per trade, which is close to real transaction costs in futures trading.
2.4.2 Pound-Dollar exchange rate
This section describes how the excess return of a trading strategy applied to an exchange rate Et is computed. On a buy signal the foreign currency is bought and the foreign risk-free interest rate rf,tF is earned. If there is a position in the foreign currency and the trading rule generates a sell signal or advises to hold no position, then the foreign currency will be exchanged for the domestic currency and the domestic risk-free interest rate rf,tD is earned. Costs are calculated as a fraction c of the exchange rate. The following formula gives the gross return of the trading strategy used:
|
|
(7) |
2.5 Profitability and predictability of trading rules
2.5.1 The best 5 strategies
Panel A of table 2.3 shows the results of the best five technical trading strategies applied to the CSCE cocoa futures price series in the period 1983:1-1997:6. Panel B of the table lists the results of the best strategy in each subperiod. The first column of the table lists the strategy parameters. MA, TRB and FR are abbreviations for the moving average, trading range break-out and filter rules respectively. %b, td, fhp, and stl are abbreviations for the %-band filter, the time delay filter, the fixed holding period and the stop-loss respectively. For example, the best technical trading strategy in the full sample period is the trading range break-out strategy with a history of five days, a two %-band filter and a 50 day fixed holding period. The second column lists the mean daily excess return of the strategy on a yearly basis, that is the mean daily return times the number of trading days in a year, which is set to 252. The third column lists the mean daily excess returns of the trading rules net of 0.1% transaction costs, with the t-ratios beneath these numbers. The t-test statistic tests whether the mean daily excess return is significantly different from zero under the assumption of iid returns. The fourth and fifth column list the number of days classified as a buy or sell day. The number of buy and sell trades is listed beneath these numbers. The sixth (seventh) column list the total number of days buy (sell) trades with a strictly positive excess return last, as a fraction of the total number of buy (sell) days. The fraction of buy and sell trades with a strictly positive excess return is listed beneath these numbers. The eight and ninth column list the mean daily return of the data series itself during buy and sell days. T-ratios to test whether the mean daily return during buy and sell days is significantly different from zero are listed beneath these numbers. In this way we can detect whether the data series itself rises during buy days and declines during sell days. The last column lists the differences between the mean daily buy and sell returns and the corresponding t-ratios, which test whether the mean daily buy return is significantly different from the mean daily sell return. These t-ratios are computed as| tB-S= |
|
, |
Notice that Brock et al. (1992) in fact do not use the correct t-test statistic, as derived in footnote 9, page 1738. To test whether the mean daily return of the DJIA during buy and sell periods is significantly different from the unconditional mean daily return it is assumed that returns are iid distributed and the following t-statistic is used: where µk is the mean return during buy or sell periods, Nk is the number of buy or sell days, µ is the mean market return, s2 is the variance of the daily returns and N is the total number of observations. However the variance of µk-µ is equal to
|
(9) |
The best strategy applied to the full sample has a significantly positive mean daily excess return of 0.039%, 10.38% yearly, which is considerably large. The mean daily excess return of the CSCE series during buy (sell) days is equal to 0.056% (-0.101%), 15.2% (-22.5%) yearly. The mean daily sell return is significantly negative at a 5% significance level using a one tailed test, while the mean daily buy return is not significantly positive. The mean buy-sell difference is significantly positive at a 5% significance level and equal to 0.158% (48.9% yearly). The four other strategies yield similar results. The mean daily excess return is significantly positive in all cases at a 10% significance level using a one tailed t-test. The mean return of the CSCE series during buy days is positive, but not significant, and the mean return during sell days is significantly negative. For all five strategies the mean buy-sell differences are significantly positive at a 5% significance level using a one sided test. The sixth and seventh column show that for all five listed strategies more than 50% of the buy and sell trades have a strictly positive excess return and that these trades consist of more than 50% of the total number of buy and sell days. The results above show that the best five technical trading strategies applied to the CSCE series in the period 83:1-97:6 have an economically as well as a statistically significant forecasting power.
For the three subperiods similar results are found, but now the best five strategies found have a higher mean daily excess return. The best strategy has a significantly positive mean yearly excess return of about 20%. Thus when looking at subperiods, strategies can be found that perform better than when applied to the full period.
Panel A of table 2.4 shows the results of the best five technical trading strategies applied to the LIFFE cocoa series in the period 83:1-97:6. Now the best five strategies consist entirely of moving-average trading strategies. The best strategy is a MA strategy that compares the price series with a 40-day MA. The strategy is extended with a 0.5 %-band filter. The results of the mean daily excess returns and the mean daily buy and sell returns are similar to the CSCE cocoa series in the same period, but the mean excess returns are higher and the t-ratios show that the results are strongly significant. The results for the number of trades with a strictly positive excess return differ. Now in most cases 20-40% of the buy and sell trades generate an excess return, but these trades consists of more than 70% of the total number of buy and sell days. Thus most of the time the strategies are making a positive excess return, but there are a lot of short run trades that make a loss.
Also for the three subperiods of the LIFFE series it is found that the best strategies perform better than the best strategy applied to the total period. But for the three subperiods the best five strategies generate buy and sell trades that are in more than 50% of the cases profitable and these trades consist of more than 70% of the total number of buy and sell days in most cases. The above results show that also for the LIFFE series the best five strategies have an economically and statistically significant forecasting power in all periods.
Table 2.5 shows the results of the best technical trading strategies applied to the Pound-Dollar exchange rate for the full sample. The best strategy is a 100 day trading range break-out rule with a one %-band filter and a 50 day fixed holding period. This strategy has a mean daily excess return of 0.007% (1.64% yearly). The mean daily return during buy (sell) days of the Pound-Dollar series itself is equal to 0.161% (-0.017%), which corresponds to 50% (-4.2%) on a yearly basis. The mean daily buy return is significantly positive in all cases, but the mean daily sell return is not significantly negative for most of the best five strategies. The mean buy-sell difference is significantly positive for all best five strategies and for the best strategy equal to 0.178% (56.6% yearly). All strategies generate buy trades with a strictly positive excess return in more than 50% of the cases, and these trades consist of more than 50% of the total number of buy days. The percentage of sell trades with a strictly positive excess return is equal to zero, because in the case of a sell trade, the domestic currency is bought and the domestic interest rate is earned. Hence the excess return during sell days is always equal to zero. The results for all three subperiods are similar. Thus also in the case of the Pound-Dollar exchange rate the results show that the best five technical trading strategies have an economically and statistically significantly forecasting power. However the mean daily excess returns of the best five strategies are smaller in comparison with the excess returns of the best five strategies applied to the cocoa series, and much less profits could be made in comparison with the cocoa series.
We have found technical trading rules that perform very well when applied to the CSCE and LIFFE cocoa futures series and the Pound-Dollar exchange rate. However, there will always be a strategy that generates a large profit if a large set of trading rules is tested as we have seen in the results above. In practice technical traders will optimize their set of trading rules and use the best one for future forecasting. Therefore Brock et al. (1992) and Levich and Thomas (1993) test a small set of strategies that are used in practice. In their bootstrap procedure which corrects for data snooping Sullivan et al. (1999) only use the best strategy. Instead, in the next section, to deal with the data snooping problem we shall look at the forecasting results of the 5350 constructed technical trading rules as a group.
2.5.2 The set of 5350 trading rules: economic significance
Cocoa futures series
We test for economic significance of the set of technical trading strategies by looking at the percentage of strategies that generate a strictly positive excess return. These numbers are shown in table 2.6 in the case of no transaction costs and in table 2.7 in the case of 0.1% transaction costs, for the CSCE, LIFFE and Pound-Dollar series, for all sets of technical trading rules and for all periods. Comparing table 2.6 with table 2.7 shows that after correcting for transaction costs, the percentage of trading rules generating a strictly positive excess return declines substantially. In the full period 83:1-97:6 the complete set of trading rules performs very well on the LIFFE cocoa futures prices, but much worse on the CSCE cocoa prices; 58.34% of the strategies generate a strictly positive excess return when applied to the LIFFE series, but only 12.18% generate a strictly positive excess return when applied to the CSCE series, after correcting for transaction costs. This large difference is remarkable, because the underlying asset in both markets is the same, except for small differences in quality of the cocoa. The table shows that the good results for the LIFFE series mainly appear in the first subperiod 1983:1-1987:12, where 73.25% of the rules generate a strictly positive net excess return for the LIFFE series against 14.14% for the CSCE series. In the second subperiod, 1988:1-1992:12, the trading rules seem to work equally well and fairly well on both series, although the results for the LIFFE series are now weaker than in the first subperiod, with 50.55% (53.90%) of the rules generating a strictly positive net excess return for the CSCE (LIFFE) series. In the third subperiod 1993:1-1997:6, the trading rules perform poorer on both series, since only 15.19% (29.25%) generate a strictly positive net excess return for the CSCE (LIFFE) series. As can be seen in the tables, the results for the different subsets of technical trading rules do not differ from the complete set of trading rules for all periods.Pound-Dollar exchange rate
For the full sample the trading rules do not show much economically significant forecasting power, with only 10.14% of the trading rules generating a strictly positive excess return net of 0.1% transaction costs. The same result is found for the first subperiod, with 9.32% generating a strictly positive net excess return. The trading rules seem to work better when they are applied to the Pound-Dollar exchange rate in the second subperiod, with 30.81% of the trading rules generating a strictly positive net excess return. In the third subperiod the strategies work badly and only 2.07% generate a strictly positive net excess return. Thus for all three data series it is found that the set of technical trading strategies performs poorly in the subperiod 1993:1-1997:6, when compared with the preceding period 83:1-92:12.Notice that, for example under the null hypothesis of a random walk, the net excess return of technical trading rules will be negative due to transaction costs. The fact that a large set of technical trading rules generates a strictly positive net excess return, especially for the LIFFE cocoa futures series, is therefore surprising and suggestive of economically significant profit opportunities. It is hard however, to evaluate the statistical significance of this observation. Therefore, in the next subsection we focus on the question whether the forecasting power of returns is statistically significant.
2.5.3 The set of 5350 trading rules: statistical significance
2.5.3.1 Significance under the assumption of iid returns: simple t-ratios
We test for the statistical forecasting significance of the set of technical trading rules by looking at the percentage of strategies which have a mean excess return, mean buy return, mean sell return, mean buy-sell difference significantly different from zero. Table 2.8 summarizes the results. The table shows for both the LIFFE and CSCE cocoa futures series and the Pound-Dollar exchange rate series for the full sample period 1983:1-1997:6 as well as for the three five year subperiods the percentages of MA, TRB and Filter trading rules, and the percentage of the complete set of trading rules for which a statistically significantly positive mean excess return is found. The table also shows the percentage of strategies that have a significantly positive (negative) mean return during buy (sell) days. Further the table shows the percentage of strategies for which the difference in mean return of the data series during buy and sell days is significantly positive. Finally, the percentage of strategies for which the data series at the same time has a significantly positive mean return during buy days as well as a significantly negative mean return during sell days is shown. A correction is made for 0.1% transaction costs.Table 2.9 shows in contrast to table 2.8 the percentage of strategies which generate statistically significant bad results, i.e. the percentage of strategies with a significantly negative mean excess return, with a significantly negative (positive) mean buy (sell) return, with a significantly negative mean buy-sell difference and the percentage of strategies which have a significantly negative mean buy return as well as a significantly positive mean sell return. These statistics are computed to test whether technical trading rules as a group show statistically significant bad forecasting power.
The tables lists only the results of one sided tests with a 10% significance level, the results for a 5% significance level are similar but of course weaker. For a 1% significance level most significant results disappear.
Cocoa futures series
For the full sample period the strategies applied to the CSCE cocoa series show hardly any statistically significant forecasting power. For example, the difference in mean return during buy and sell days is significantly positive only in 1.38% of the trading rules, whereas a significantly negative mean return during sell days occurs only in 5.92% of all strategies. Only in 0.3% of the cases the mean excess return is significantly positive, hence no significant profits could be made. For the LIFFE series on the other hand the results are remarkably different. For 26.58% of the strategies the mean buy-sell difference is significantly positive. In particular, the strategies seem to forecast the sell days very well, with more than half (50.53%) of all strategies having a significantly negative mean return during sell days. In contrast, the mean buy return is significantly positive only in 6.86% of all strategies. 13.86% of the strategies have a significantly positive mean excess return when applied to the LIFFE series. Looking at table 2.9 a lot of strategies perform statistically very bad when applied to the CSCE series, while the percentage of strategies that performs statistically badly is much less for the LIFFE series. Thus for the full sample the set of strategies applied to the LIFFE series shows a lot of economic significance, which is also statistically significant, and a lot of trading rules have a statistically significant forecasting power, i.e. they detect periods in which the data series rises and declines, while the percentage of trading rules which performs statistically badly is smaller than the percentage of trading rules which performs statistically good.For the first subperiod the trading rules show almost no statistically significant forecasting power when applied to the CSCE series. Most t-ratios stay within the critical values. The percentage of strategies that perform badly is even larger than the percentage of strategies that perform well. For example 24.17% of all strategies generate a significantly negative mean excess return. For the LIFFE series the results are totally different. All subsets of trading rules show some forecasting power. 34.52% of all strategies generate a significantly positive mean excess return. For 26.73% of the strategies the mean return of the data series during buy days is significantly positive, for 39.47% of the strategies the mean return during sell days is significantly negative and for 46.65% of the strategies the Buy-Sell difference is significantly positive. The percentage of strategies that performs statistically badly is small. For 5.87% of the strategies the mean excess return is significantly negative. Hence, for the LIFFE series the trading rules show economic as well as statistically significant forecasting power in the first subperiod.
The second subperiod is characterized by a long term downward trend with short term upward corrections in both cocoa series. Economically the strategies behave quite well in the second subperiod, but the statistical significance of the mean excess return of the strategies is very poor (CSCE: 1.85%>tcrit; LIFFE 6.31%>tcrit). Hence the economic significance found is not statistically significant. All subsets of trading rules show a significantly negative mean return of the data series during sell days (CSCE: 44.57%<-tcrit; LIFFE: 54.62%<-tcrit), which is in line with the downward trend. The upward corrections are not predicted well by the strategies, and for many trading rules the mean return of the data series during buy days is even significantly negative (CSCE: 26.55%<-tcrit; LIFFE: 31.96%<-tcrit). The results found for the second subperiod are in line with the advices of technical analysts only to trade in the direction of the main trend and not reverse the position in the market until there is enough weight of evidence that the trend has reversed. Apparently, the short term upward corrections did not last long enough to be predictable or profitable.
The third subperiod is characterized by upward and downward trends in prices. The trading rules show no economic significance for this period and neither do they show statistical forecasting significance. 29.25% of the strategies applied to the LIFFE series generated a strictly positive excess return, but only for 2.13% of the strategies the mean excess return is significantly positive. For the CSCE series even 32.26% of the strategies generate a significantly negative mean excess return. If there was any predictability in the data it has disappeared in the third subperiod.
Pound-Dollar exchange rate
For the full sample 83:1-97:6 table 2.8 shows that 13.08% of the strategies have a significantly positive mean buy return and 17.13% have a significantly negative mean sell return. In 28.19% of the cases the mean Buy-Sell difference is significantly positive. Thus the trading rules seem to generate good trading signals. However, the mean excess return is significantly positive only in 2.07% of the trading rules, while even in 62.32% of the cases the trading rules generate a significantly negative mean excess return. Especially the moving-average trading rules perform badly.For the first subperiod the results are similar (Buy: 12.42%>tcrit; Sell: 44.29%<-tcrit; Buy-Sell: 41.9%>tcrit). Sell days are forecasted much better than the buy days. However, only for 0.35% of the strategies the mean excess return is significantly positive, while in 27.11% of the cases the mean excess return is even significantly negative. According to the Buy-Sell difference the trading rules as a group seem to have a statistically significant forecasting power in this period, but the economic significance is poor.
In the second subperiod the strategies forecast the upward trends better than the downward trends, 29.63% of the strategies have a significantly positive mean buy return, while 7.73% of the trading rules have a significantly negative mean sell return. For 26.13% of the trading rules the Buy-Sell difference is significantly positive. Only 4.78% of the strategies have a significantly positive mean excess return, while even 17.32% of the strategies have a significantly negative mean excess return. Hence, also in this subperiod there are signs of forecastability according to the Buy-Sell difference, which cannot be exploited economically.
In the third subperiod the Pound-Dollar exchange rate exhibits some upward and downward trends. The trading rules show hardly any signs of forecasting power in this subperiod for the Pound-Dollar exchange rate. Only in 0.09% of the cases a significantly positive mean excess return is generated, while in 66.02% of the cases a significantly negative mean excess return is generated.
2.5.3.2 Significance after correction for dependence: an estimation based approach
In the previous subsection we showed that in the period 1983:1-1987:12 the technical trading strategies as a group seem to have forecasting power when applied to the LIFFE cocoa futures prices. This is the only period and data series for which good results in favor of technical analysis are found. We tested on statistical significance under the assumption of iid returns. It is well known, however, that returns show dependence in the second moments (volatility clustering) and in section 2.2.3 we showed that our data series also exhibit some autocorrelation. Therefore we further explore the statistical significance found in the first subperiod by estimating for each trading rule an econometric time series model which incorporates volatility clustering, autoregressive variables and a dummy for buy (sell) days in the regression function. We then determine the percentage of cases for which the dummy coefficients are significant, to check whether the trading rules as a group show signs of forecasting power.We estimated some econometric time series models on the daily LIFFE cocoa return series for the period 1983:1-1987:12 and we find that the following exponential GARCH model developed by Nelson (1991)8 fits the data best9:
|
(10) |
To explore the significance of the trading rules after correction for dependence the following regression function in the exponential GARCH model is estimated:
Table 2.10: Coefficient estimates EGARCH-model
Estimates on the daily return series of the LIFFE cocoa futures prices in the period December 12th 1981 until December 31, 1987. The exponential GARCH model is estimated using maximum likelihood using the Marquardt iterative algorithm and Bollerslev-Wooldridge (1992) heteroskedasticity-consistent standard errors and covariance. The numbers within parenthesis are t-ratios.
a f16 a0 q g b1
-0.000339 0.066843 -0.194617 0.037536 0.125153 0.976722 (-1.11) (2.49) (-2.83) (2.11) (3.41) (97.58)
rt=a + dm Dm,t + f16 rt-16 + et,
where m=B (m=S) indicates that we insert a dummy for buy (sell) days, and we will refer to Dm,t as the buy (sell) dummy. Thus DB,t=1 (DS,t=1) if day t is a buy (sell) day. For every trading strategy the coefficient for the buy dummy and for the sell dummy are estimated separately. Panel A of table 2.11 shows the percentage of trading rules for which the coefficient of the buy (sell) dummy is significantly positive (negative) at the 10% significance level (second and third column) using a one tailed t-test. The fourth column shows the percentage of trading rules for which the coefficient of the buy dummy is significantly positive and the coefficient of the sell dummy is significantly negative. The results again indicate that the technical trading strategies have forecasting power in the first subperiod. For 40.6% of all trading rules we find that the coefficient of the buy dummy is significantly positive. 27.4% of all trading rules show a significantly negative coefficient of the sell dummy. Finally, 22.8% of all trading rules have a significantly positive coefficient of the buy dummy as well as a significantly negative coefficient of the sell dummy. Panel B of table 2.11 shows that the strategies as a group do not perform statistically badly. For example 1.6% of all trading rules show a significantly negative coefficient of the buy dummy as well as a significantly positive coefficient of the sell dummy. This number is small compared to the 22.8% of the strategies that show statistically significant forecasting power. In comparison with the tests under the assumption of iid returns, it now seems that the trading rules forecast the buy days better than the sell days, while first it was the other way around. 2.6 Bootstrap
2.6.1 Bootstrap tests: methodology
The results reported in the last section show again that simple trend-following technical trading techniques have forecasting power when applied to the LIFFE series in the period 1983:1-1987:12. In this section we investigate whether the good results found can be explained by some popular time series models like a random walk, autoregressive or an exponential GARCH model using a bootstrap method.The bootstrap methodology compares the percentage of trading rules with a significantly positive mean buy return, with a significantly negative mean sell return, with a significantly positive mean buy-sell difference and with a significantly positive mean buy as well as a significantly negative mean sell return, when applied to the original data series, with the percentages found when the same trading rules are applied to simulated comparison series. The distributions of these percentages under various null hypotheses for return movements will be estimated using the bootstrap methodology inspired by Efron (1982), Freedman (1984), Freedman and Peters (1984a, 1984b), and Efron and Tibshirani (1986). According to the estimation based bootstrap methodology of Freedman and Peters (1984a, 1984b) a null model is fit to the original data series. The estimated residuals are standardized and resampled with replacement to form a new residual series. This scrambled residual series is used together with the estimated model parameters to generate a new data series with the same properties as the null model.
For each null model we generate 500 bootstrapped data series. The set of 5350 technical trading rules is applied to each of the 500 bootstrapped data series to get an approximation of the distributions of the percentage of strategies with a significantly positive mean buy return, with a significantly negative mean sell return, with a significantly positive buy-sell difference and with a significantly positive mean buy as well as a significantly negative mean sell return under the null model. The null hypothesis that our strong results found can be explained by a certain time series model is rejected at the a percent significance level if the percentage found in the original data series is greater than the a percent cutoff level of the simulated percentages under the null model.
Random walk process
The random walk with a drift is bootstrapped by resampling the returns of the original data series with replacement. If the price series is defined as {Pt: t=1,2,...,T}, then the return series is defined as {rt=ln(Pt)-ln(Pt-1): t=2,3,...,T}. Finally the bootstrapped price series is equal to {Pt*=exp(rt*) Pt-1*: t=2,3,...,T}, where rt* is the redrawn return series. The initial value of the bootstrapped price series is set equal to the initial original price: P1*=P1. By construction the returns in the bootstrapped data series are iid. There is no dependence in the data anymore that can be exploited by technical trading rules. Only by chance a trading rule will generate good forecasting results. Hence under the null of a random walk with a drift we test whether the results of the technical trading rules in the original data series are just the result of pure luck.Autoregressive process
The second null model we test upon is an AR model: where rt is the return on day t and et is iid10. The coefficients a, f16 and the residuals et are estimated with ordinary least squares. The estimated residuals are redrawn with replacement and the bootstrapped return series are generated using the estimated coefficients and residuals:rt*=a + f16 rt-16* + et*,
for t=18,...,T and where et* is the redrawn estimated residual at day t and where rt* is the bootstrapped return at day t. For t=2,..,17 we set rt*=rt. The bootstrapped price series is now equal to {Pt*=exp(rt*) Pt-1*: t=2,...,T} and P1*=P1. The autoregressive model tests whether the results of the technical trading strategies can be explained by the high order autocorrelation in the data. OLS estimation with White's (1980) heteroskedasticity-consistent standard errors gives the following results with t-ratios within parenthesis:
| a | f16 | |
| -0.000235 | 0.110402 | |
| (-0.68) | (4.00) | |
Exponential GARCH process
The third null model we test upon is the exponential GARCH model as given by (2.10). The model is estimated with maximum likelihood. The estimated coefficients and standardized residuals are used to generate new bootstrapped price series. The estimated standardized residuals, ht, are resampled with replacement to form the resampled standardized residual series {ht*: t=18,...,T}. The bootstrapped log conditional variance series is equal to{ln(ht*)=a0+g(ht-1*)+b1 ln(ht-1*):t=19,...,T }.
We set h18* equal to the unconditional variance. Under the assumption that the ht are iid N(0,1) the unconditional variance of et is equal to
| E(ht)={exp(a0) E[exp | (g(ht-1))]} |
|
, |
|
{et*=ht* ht*: t=19,...,T} and the bootstrapped return series is equal to
{rt*=a+f16 rt-16*+et*: t=19,...,T}. For t=2,...,18 we set rt*=rt. The bootstrapped price series is equal to {Pt*=exp(rt*) Pt-1*: t=2,...,T} and P1*=P1. Table 2.10 contains the estimation results for the exponential GARCH model.
Structural break in trend
 |
| Figure 2.4: Time series, over the period 1983:1-1987:12, of CSCE (top left) and LIFFE (middle left) cocoa futures prices on the same scale [800, 2200], the Pound-Dollar exchange rate on scale [0.8, 2.2] (bottom left) and corresponding returns series (right) all on the same scale [-0.08, 0.06]. |
|
The returns in the first period show significantly positive 16-th order autocorrelation, while the returns in the second period show significantly negative second order autocorrelation. The constant is in the first period significantly positive at the 10% significance level, while in the second period it is significantly negative at the 1% significance level. This is an indication that the drift is first positive and then negative. With this final bootstrap procedure we can test whether the good results of the technical trading rules can be explained by the trend structure in the data series and the strong autocorrelation in returns.
Table 2.12: Coefficient estimates structural break in trend model
Estimates of an autoregressive model on the daily return series of the LIFFE cocoa futures prices in the period January 5, 1983 until February 4, 1985 and of a GARCH model in the period February 5, 1985 until December 31, 1987. The autoregressive model is estimated using OLS and White's (1980) heteroskedasticity-consistent standard errors. The GARCH model is estimated using maximum likelihood using the Marquardt iterative algorithm and Bollerslev-Wooldridge (1992) heteroskedasticity-consistent standard errors and covariance. The numbers within parenthesis are t-ratios.
The autoregressive model coefficients estimates 1/5/1983 - 2/4/1985 a f16
0.001213 0.161887 (1.74) (3.67)
The GARCH-model coefficients estimates 2/5/1985 - 12/31/1987 a f2 a0 a1 b1
-0.001511 -0.113115 3.85E-06 0.064247 0.905622 (-3.95) (-2.85) (1.48) (1.68) (18.6)
2.6.2 Bootstrap tests: empirical results
Random walk process
In table 2.13 we display the bootstrap results under the null of a random walk, an autoregressive model, an exponential GARCH model and the structural break in trend model when the complete set of technical trading strategies is applied to the LIFFE cocoa futures prices in the period 1983:1-1997:6. All the results presented are the fractions of simulation results that are larger than the results for the original data series. In panel A the fractions of the 500 bootstrapped time series are reported for which the percentage of trading rules with a significantly positive mean excess return, with a significantly positive mean buy return, with a significantly negative mean sell return, with a significantly positive mean buy-sell difference, and with a significantly positive mean buy as well as significantly negative mean sell return at a ten percent significance level using a one sided t-test is larger than the same percentage found when the same trading rules are applied to the original data series. Panel B on the other hand reports the bootstrap results for the bad significance of the trading rules. It shows the fraction of the 500 bootstrapped time series for which the percentage of trading rules with a bad significance is even larger than the percentage of trading rules with a bad significance at a 10% significance level using a one sided t-test when applied to the original data series.For the cocoa series the mean excess return is approximately equal to the return on the futures position without correcting for the risk-free interest rate earned on the margin account, because
| rte =ln(1+rtf + |
|
Post)-ln(1+rtf) » rtf + |
|
Post -rtf = |
|
Post. |
We have already seen in table 2.8 that for 34.5% of the strategies the mean excess return is significantly positive in the first subperiod for the LIFFE cocoa futures series. The number in the column of the random walk results in the row tPerf>tc, which is 0.002, shows that for 0.2% of the 500 random walk simulations the percentage of strategies with a significantly positive mean excess return is larger than the 34.5% found when the strategies are applied to the original data series. This number can be thought of as a simulated ``p-value''. Hence the good results for the excess return found on the original data series cannot be explained by the random walk model. For 26.7% of the strategies the mean buy return is significantly positive. The fraction in the row tBuy>tc shows that in only 3.2% of the simulations the percentage of strategies with a significantly positive mean buy return is larger than the 26.7% found in the original data series. However, the fraction in the row tSell<-tc, shows that in 14% of the simulations the percentage of strategies with a significantly negative mean sell return is larger than the 39.5% of strategies with a significantly negative mean sell return when applied to the original data series. Thus the random walk model seems to explain the significantly negative mean sell return. For 46.7% of the strategies the buy-sell difference is significantly positive, but the fraction in the row tBuy-Sell>tc shows that for none of the random walk bootstraps the percentage of trading rules with a significantly positive mean buy-sell return is larger than this number. 14.7% of the strategies have a significantly positive mean buy return as well as a significantly negative mean sell return. The number in the row tBuy>tc Ù tSell<-tc, which is 0.006, shows that in only 0.6% of the simulations this percentage is larger than the 14.7% found in the original data series.
Table 2.9 showed the percentage of strategies with a bad significance when applied to the original data series. For the LIFFE cocoa futures series in the first subperiod the strategies as a group show no real signs of bad significance. For 5.9% of the strategies the mean excess return is significantly negative, for 3.5% of the strategies the mean buy return is significantly negative, for 3.3% of the strategies the mean sell return is significantly positive, for 3.3% of the strategies the mean buy-sell difference is significantly negative and for 0.82% of the strategies the mean buy return is significantly negative and also the mean sell return is significantly positive. Panel B of table 2.13 shows that under the null of a random walk the strategies as a group perform even much worse. The number in the row tPerf<-tc shows that for 96.4% of the simulations the percentage of strategies with a significantly negative mean excess return is larger than the 5.9% found in the original data series. For 87% of the simulations the percentage of strategies with a significantly negative mean buy return is larger than the 3.5% found on the original data series. For 57.2% (96.8%, 34.2%) of the simulations the percentage of strategies with a significantly positive mean sell (significantly negative mean buy-sell difference, a significantly negative mean buy as well as a significantly positive mean sell return) is larger than the 3.3% (3.3%,0.82%) found in the original data series.
From the results reported above we can conclude that the good results found when the technical trading strategies are applied to the LIFFE cocoa futures prices in the period 1983:1-1997:6 cannot be explained by a random walk model.
Autoregressive process
The third column of table 2.13 repeats the previous results under the null of an autoregressive process. Now we can detect whether the good results of the technical trading strategies can be explained by the high order autocorrelation in the data. The results change indeed in comparison with the null of a random walk. Now for 3.8% of the 500 AR bootstraps the percentage of strategies with a significantly positive mean excess return is larger than the 34.5% found in the original data series. For 7.4% (27.4%) of the simulations the percentage of strategies with a significantly positive mean buy return (significantly negative mean sell return) is larger than the 26.7% (39.5%) found in the original data series. Hence the autoregressive model seems to explain the good significant results of the technical trading rules as a group for selecting buy and sell days. On the other hand the autoregressive model does not explain the results found for the percentage of strategies with a significantly positive mean buy-sell difference and the percentage of strategies with a significantly positive mean buy as well as a significantly negative mean sell return. Panel B shows again, as in the case of the null of a random walk, that the strategies as a group perform much worse on the simulated autoregressive data series than on the original data series. We can conclude that the autoregressive model neither can explain the good results of the technical trading rules.Exponential GARCH process
The results of the bootstrap procedure under the null of an exponential GARCH model are similar to those under the null of an autoregressive model. Therefore the good results of the technical trading strategies can also not be explained by the leverage effect, which is accounted for in the exponential GARCH formulation.Structural break in trend
The last column of table 2.13 lists the bootstrap results of applying the set of trading strategies to simulated autoregressive series with a structural change to account for the different trending behavior of the LIFFE cocoa futures prices. The results change completely in comparison with the other null models. For 41.4% of the simulations the percentage of strategies with a significantly positive mean excess return is larger than the 34.5% found when the same set is applied to the original data series. For 47.8% (52.8%, 24.8%) of the simulations the percentage of strategies with a significantly positive mean buy (significantly negative mean sell, significantly positive mean buy-sell difference) return is larger than the 26.7% (39.5%, 46.7%) found when the same set is applied to the original data series. Even for 42.6% of the simulations the percentage of strategies with a significantly positive mean buy as well as a significantly negative mean sell is larger than the 14.7% found for the original data series. Hence the final model, which allows a structural change, because there is first an upward trend and then a downward trend in the price series, seems to explain the good results found when the set of technical trading strategies is applied to the LIFFE cocoa futures price series in the period 1983:1-1987:12. Probably the trading rules performed well because of the strong trends in the data. Panel B shows the bootstrap results for testing whether the bad significance of the technical trading rules can be explained by the several null models. In the case of the structural break in trend model the results show again that the set of technical trading rules behaves statistically worse when applied to the simulated series than to the original data series. For example in 96% of the simulations the percentage of strategies with a significantly negative mean excess return is larger than the 5.9% found when the same strategies are applied to the original data series. Despite that the structural break in trend model can explain the statistically significant forecasting power of the trading rules, also this model cannot explain the good results found when testing for bad significance of the strategies in the original data series. Thus the original time series has characteristics which causes the trend-following technical trading techniques to show signs of forecasting power, most probably the characteristic of the strong change in direction of the price trend. However this characteristic is not the only explanation, because it cannot explain the relatively low percentage of trend-following technical trading techniques which performed statistically badly on the original time series.2.7 Success and failure of technical trading
The technical trading strategies as a group show economic and statistically significant forecasting power when applied to the LIFFE cocoa series, especially in the period 1983:1-1987:12. On the other hand the same technical trading strategies show no sign of forecasting power when applied to the CSCE cocoa series in the same period. The futures contracts differ in their specification of quality, currency and place of delivery, but it is surprising that the difference in economic and statistical significance is so large. Why are these differences so pronounced?The daily CSCE cocoa returns show somewhat stronger autocorrelation in the first two lags than the LIFFE returns, which suggests more predictability. The variance of the CSCE series is slightly bigger across all subperiods than the variance of the LIFFE series, which may be an indication why trend-following rules have more difficulty in predicting the CSCE cocoa series. However, it seems that this somewhat higher variance cannot explain the large differences. For example, in the second subperiod, when the volatility is the strongest across all subperiods for both time series, the trading rules perform almost equally well on the CSCE and LIFFE cocoa futures prices and show forecasting power of the sell days for both series. Hence, there must be some other explanation for the differences of technical trading performance.
Figure 2.3 already showed that, in the period 1983:1-1987:12, the LIFFE and CSCE cocoa futures prices first exhibit an upward trend from 83:1-84:6 for the CSCE in New York and from 83:1-85:2 for the LIFFE in London, whereas from 85:2-87:12 both cocoa series exhibit a downward trend. The upward trend until mid 84 was due to excess demand on the cocoa market, whereas after January 1986 cocoa prices declined for several years due to excess supply. See for example the graphs of gross crops and grindings of cocoa beans from 1960-1997 in the International Cocoa Organization Annual Report 1997/1998 (see e.g. p.15, Chart I).11 The demand-supply mechanism thus caused the upward and downward trends in cocoa futures prices in the subperiod 1983:1-1987:12. Figure 2.3 suggests that these trends were more pronounced in London for the LIFFE than in New York for the CSCE.
2.7.1 The influence of the Pound-Dollar exchange rate
Figure 2.3 also showed that the Pound-Dollar exchange rate moved in similar trends in the same subperiod 1983:1-1987:12. More precisely, the Pound-Dollar exchange rate increased (the Pound weakened against the Dollar) from January 1983 to reach its high in February 1985. This caused an upward force on the LIFFE cocoa futures price in Pounds, and a downward force on the CSCE cocoa futures price in Dollars. The LIFFE cocoa futures price also peaked in February 1985, while the CSCE cocoa futures price reached its high already in June 1984. After February 1985, the Pound strengthened against the Dollar until April 1988 and the Pound-Dollar exchange rate declined. This caused a downward force on the LIFFE cocoa futures price in Pounds, but an upward force on the CSCE futures price in Dollars. Until January 1986 the LIFFE cocoa price declined, while the CSCE cocoa price rose slightly. After January 1986 cocoa prices fell on both exchanges for a long time, due to excess supply of cocoa beans. We therefore conclude that, by coincidence, the upward and downward trends in the cocoa prices coincide with the upward and downward trends in the Pound-Dollar exchange rate. For the LIFFE in London the trends in exchange rates reinforced the trends in cocoa futures, whereas for the CSCE in New York the trends in the exchange rates weakened the trends in cocoa futures prices.Table 2.14 shows the cross-correlations between the levels of the three data series across all subperiods. It is well known that if two independently generated integrated time series of the order one are regressed against each other in level, with probability one a spurious, but significant relation between the two time series will be found (Phillips 1986). Although the Pound-Dollar exchange rate should be independently generated from the cocoa futures series, it has some impact on the price level of the cocoa series as described above. The table shows that the Pound-Dollar exchange rate is correlated strongly with the level of the LIFFE cocoa continuation series and also (although a little bit weaker) with the CSCE cocoa continuation series. In particular, in the first subperiod 1983:1-1987:12 the Pound-Dollar exchange rate is correlated strongly with the level of the LIFFE cocoa futures series (cross correlation coefficient 0.88) and also (although a little bit weaker) with the CSCE cocoa futures series (cross correlation coefficient 0.58). In the other subperiods, there is little cross correlation between the Pound-Dollar exchange rate and the LIFFE and/or the CSCE cocoa futures series.
Apparently, due to the accidental correlation (spurious relation) in the period 1983:1-1987:12 between the Pound-Dollar exchange rate movements and the demand-supply mechanism in the cocoa market, trends in the LIFFE cocoa futures price are reinforced and trends in the CSCE cocoa futures price are weakened. Because the technical trading rules we tested are mainly trend-following techniques, this gives a possible explanation for the large differences in the performance of technical trading in the LIFFE and CSCE cocoa futures.
In order to explore further the possible impact of the Pound-Dollar exchange rate on the profitability of trend-following technical trading techniques when applied to the cocoa data series, we test the trading rules on the LIFFE cocoa price series expressed in Dollars and on the CSCE cocoa price series expressed in Pounds. If the LIFFE and CSCE cocoa futures prices are expressed in the other currency, then the results of testing technical trading strategies change indeed. In order to test for economic significance table 2.15 lists the percentage of trading rules with a strictly positive mean excess return for all trading rules sets across all subperiods. For the full sample, 83:1-97:6, for the LIFFE cocoa series in Dollars 33.85% (versus 58.34% in Pounds) of all trading rules generate a strictly positive mean excess return, while for CSCE cocoa futures in Pounds 19.30% (versus 12.18% in Dollars) of the trading rules generate a strictly positive mean excess return. Especially in the first subperiod 1983:1-1987:12 the results change dramatically. For the LIFFE cocoa series in Dollars 23.71% (versus 73.25% in Pounds) of all trading rules generate a strictly positive mean excess return, while for CSCE cocoa futures in Pounds 57.93% (versus 14.14% in Dollars) of the trading rules generate a strictly positive mean excess return.
Table 2.16 summarizes the results concerning the statistical forecasting power of the trading rules applied to the LIFFE cocoa futures in Dollars and the CSCE cocoa futures in Pounds. The table shows for all periods for both data series the percentage of trading rules generating a significantly positive mean excess return. The table also shows the percentage of trading rules generating a significantly positive (negative) mean return during buy (sell) days. Further the table shows the percentage of trading rules for which the mean Buy-Sell difference of the data series is significantly positive and for which buy and sell days at the same time generate significantly positive respectively negative returns. The table summarizes only the results of one sided tests at the 10% significance level. The results of table 2.16 should be compared to the corresponding results of table 2.8.
For the full sample, the statistical properties of the trading rules applied to the CSCE cocoa series in Pounds are only slightly better than for the CSCE cocoa series in Dollars. For example, only 2.73% (versus 1.38%) of all rules yields a significantly positive difference between Buy-Sell returns. The sell days are predicted better, with 14.25% (versus 5.92% of the trading rules showing significantly negative mean return during sell days. For the LIFFE series in Dollars the statistical results of the trading rules are poorer than for to the LIFFE series in Pounds. Now only 1.31% of the strategies generate a significantly positive mean excess return, while this percentage is 13.86% for the LIFFE series in Pounds. The mean Buy-Sell difference is significantly positive only for 5.10% (versus 26.58%) of all trading rules. The trading rules still forecast the sell days well, with 25.97% of the trading rules having significantly negative mean return during sell days, but not nearly as good as for the LIFFE cocoa series in Pounds for which 50.53% of all rules has significantly negative mean return during sell days.
For the first subperiod the trading rules showed no statistically significant forecasting power on the CSCE series in Dollars. When applied to the CSCE series in Pounds the results are much better. For example 8.33% (versus 0.92%) of the strategies has a significantly positive mean excess return. 19.65% (versus 0.77%) of all trading rules has a significantly negative mean return during sell days. For the buy days most t-ratios stay within the critical values and only 6.13% (versus 1.27%) has significantly positive returns. For 19.41% (versus 1.46%) of all strategies the mean Buy-Sell difference is significant. The strongly significant forecasting power of the strategies applied to the LIFFE series in Pounds totally vanishes when applied to the LIFFE series in Dollars. The percentage of trading rules which generates a significantly mean excess return decreases from 34.52% to 1.03%. For most trading rules the t-ratios of the mean return of the data series during buy or sell days stay within the critical values. Only 1.18% (versus 39.47%) of all trading rules has a significantly negative mean return during sell days and only 1.70% (versus 26.73%) has significantly positive returns during buy days. The percentage of strategies for which the mean Buy-Sell difference is significant drops from 46.65% to 2.13%.
We conclude that, especially in the first subperiod, the Pound-Dollar exchange rate had a strong influence on the forecasting power of the trading rules applied to the LIFFE cocoa futures price in Pounds. There is a dramatic change in predictability when the LIFFE cocoa futures price is transformed to Dollars. On the other hand the forecasting power of the strategies on the CSCE cocoa series transformed to Pounds is not as strong as the forecasting power of the strategies applied to the LIFFE cocoa series in Pounds. The Pound-Dollar exchange rate mechanism thus provides only a partial explanation, in addition to the demand-supply mechanism on the cocoa market, of the predictability of trading rules applied to cocoa futures.
2.7.2 What causes success and failure of technical trading?
An important theoretical and practical question is: ``What are the characteristics of speculative price series for which technical trading can be successful?'' In order to get some insight into this general question from our case-study, it is useful to plot the price and returns series all on the same scale, as shown in figure 2.4. The returns series clearly show that the volatility in the Pound-Dollar exchange rate is lower than the volatility in both cocoa futures series. Furthermore, the price series on the same scale show that the trends in the LIFFE cocoa series are much stronger than in the CSCE cocoa series and the Pound-Dollar exchange rate. One might characterize the three series as follows: (i) CSCE has weak trends and high volatility; (ii) LIFFE has strong trends and high volatility, and (iii) Pound-Dollar has weak trends and low volatility.Recall from section 5 that the performance of technical trading may be summarized as follows: (i) no forecasting power and no economic profitability for CSCE; (ii) good forecasting power and substantial net economic profitability for LIFFE, and (iii) good forecasting power but no economic profitability for Pound-Dollar.
Our case-study of the cocoa futures series and the Pound-Dollar exchange rate series suggest the following connection between performance of technical trading rules and the trend and volatility of the corresponding series. When trends are weak and volatility is relatively high, as for the CSCE cocoa futures series, technical trading does not have much forecasting power and therefore also cannot lead to economic profitability. Volatility is too high relative to the trends, so that technical trading is unable to uncover these trends. When trends are weak but volatility is also relatively low, as for the Pound-Dollar exchange rates, technical trading rules can have statistically significant forecasting power without economically significant profitability. In that case, because volatility is low technical trading can still pick up the weak trends, but the changes in returns, although predictable, are too small to account for transaction costs. Finally, when trends are strong and volatility is relatively high, as for the LIFFE cocoa futures series, a large set of technical trading rules may have statistically significant forecasting power leading to economically significant profit opportunities. In that case, the trends are strong enough to be picked up by technical trading even though volatility is high. Moreover, since volatility is high, the magnitude of the (predictable) changes in returns is large enough to cover the transaction costs.
2.8 Concluding remarks
In this chapter the performance of a large set of 5350 technical trading rules has been tested on the prices of cocoa futures contracts, traded at the CSCE and the LIFFE, and on the Pound-Dollar exchange rate in the period 1983:1-1997:6. The large set of trading rules consists of three subsets: 1990 moving average, 2760 trading range break-out and 600 filter strategies. The strategies perform much better on the LIFFE cocoa prices than on the CSCE cocoa prices, especially in the period 1983:1-1987:12. In this period a large group of the trading rules applied to the LIFFE cocoa futures price has statistically significant forecasting power and is economically profitable after correcting for transaction costs. Applied to the CSCE cocoa futures series the trading rules show little forecasting power and are not profitable. The forecasting power of the strategies applied to the Pound-Dollar exchange rate in the period 1983:1-1997:6 is also statistically significant, but most trading strategies are not profitable.The large difference in the performance of technical trading in the LIFFE or CSCE cocoa futures contracts may be explained by a combination of the demand/supply mechanism in the cocoa market and the Pound-Dollar exchange rate. In the period 1983:1-1987:12 the price level of the cocoa futures contracts and the level of the Pound-Dollar exchange rate were, accidentally, strongly correlated. This spurious correlation reinforced upward and downward price trends of the LIFFE cocoa futures contracts in London, while weakening the price trends of the CSCE cocoa futures contracts in New York. For the LIFFE cocoa futures price series the trends are strong enough to be picked up by a large class of technical trading rules; for the CSCE cocoa futures price series most trading rules do not pick up the trends, which are similar to the trends in the LIFFE cocoa futures but weaker. We also performed a bootstrap analysis showing that benchmark models such as a random walk, an autoregressive and an exponential GARCH cannot explain the good performance of the technical trading rules in the period 1983:1-1987:12. However a structural break in the trend model cannot be rejected as explanation of the results. Apparently many technical trading rules are able to pick up this structural break in trend. For the period 1993:1-1997:12 we find that the forecasting power of the technical trading strategies applied to the cocoa futures prices and the Pound-Dollar exchange rate is much less than in the preceding period 1983:1-1992:12. This is in line with many papers that found that forecasting power of trading strategies tends to disappear in the 1990s.
Although the present chapter only documents the economic and statistical performance of technical trading rules applied to a single commodity market, some general conclusions that may be useful for other financial series as well are suggested by our case-study. First, in order to assess the success or failure of technical trading it is useful to test a large class of trading rules, as done in this chapter. A necessary condition for reliable success of technical trading seems to be that a large class of trading rules, not just a few, should work well. If only a few trading rules are successful this may simply be due to ``chance'' or to data snooping. It should also be emphasized that even if a large class of trading rules has statistically significant forecasting power this is not a sufficient condition for economically significant trading profits after correcting for transaction costs. An example is the Pound-Dollar exchange rate for which a large fraction of trading rules exhibits statistically significant forecasting power, but these trading rules hardly generate economic net profitability.
Our case-study of the cocoa futures series and the Pound-Dollar exchange rate series suggest a connection between the success or failure of technical trading rules and the trend and volatility of the corresponding series. When trends are weak and volatility is relatively high, technical trading does not have much forecasting power and therefore also cannot lead to economic profitability. Technical trading is unable to uncover these trends, because volatility is too high. When trends are weak but volatility is relatively low, technical trading rules can have statistically significant forecasting power without economically significant profitability. In that case, because volatility is low technical trading can still pick up the weak trends, but the changes in returns, although predictable, are too small to account for transaction costs. Finally, when trends are strong and volatility is relatively high, a large set of technical trading rules may have statistically significant forecasting power leading to economically significant profit opportunities. In that case, even though volatility is high the trends are strong enough to be picked up by technical trading. Moreover, since volatility is high, the magnitude of the (predictable) changes in returns is large enough to cover the transaction costs. We emphasize that this connection between predictive and economic performance of technical trading is suggestive and only documented by the market studied here. Further research, of interest from a theoretical as well as a practical viewpoint, is needed to uncover whether the success and failure of technical trading is explained by the relative magnitudes of trend and volatility.
Technical analysis may pick up sufficiently strong trends in asset prices and even may pick up a structural break in trends, without knowing or understanding the economic forces behind these trends. It seems wise however that a technical analyst does not trust his charts only, but also tries to trace economic fundamentals that may cause or reinforce detected trends. For the LIFFE cocoa futures series the trends were caused by two forces, namely the supply-demand mechanism in the cocoa market and the exchange rate movements. Apparently, at the same time as the trend break point, these forces changed direction. If both the technical charts and fundamental indicators point in the same direction technical trading can be successful; otherwise failure seems a real possibility.
Appendix
A. Tables
| Table | |
| 2.1 | Summary statistics for daily returns |
| 2.2 | Autocorrelation functions of daily returns |
| 2.3 | Results of the best strategies applied to the CSCE cocoa futures prices |
| 2.4 | Results of the best strategies applied to the LIFFE cocoa futures prices |
| 2.5 | Results of the best strategies applied to the Pound-Dollar exchange rate |
| 2.6 | Excess returns without transaction costs |
| 2.7 | Excess returns with 0.1% transaction costs |
| 2.8 | Significance: simple t-ratios |
| 2.9 | Bad significance: simple t-ratios |
| 2.10 | Coefficient estimates EGARCH-model |
| 2.11 | Significance after correction for dependence: an estimation based approach |
| 2.12 | Coefficient estimates structural break in trend model |
| 2.13 | Significance after correction for dependence: a bootstrap based approach |
| 2.14 | Cross-correlations |
| 2.15 | Excess returns when LIFFE in Dollars and CSCE in Pounds |
| 2.16 | Significance when LIFFE in Dollars and CSCE in Pounds: simple t-ratios |
| 2.17 | Bad significance when LIFFE in Dollars and CSCE in Pounds: simple t-ratios |
Table 2.1: Summary statistics for daily returns. Results are presented for the full sample and for three subperiods. Returns are calculated as the log differences of the prices. The maximum loss is the largest consecutive decline in percentage terms during a certain period. The t-ratio tests whether the mean return is significantly different from zero.
Full Sample 83:1-87:12 88:1-92:12 93:1-97:6 CSCE N 3654 1254 1262 1136 Yearly effective return -0.078914 -0.016746 -0.21364 0.020661 Mean -0.000326 -0.000067 -0.000954 0.000081 Std. Dev. 0.016616 0.015787 0.018842 0.014773 t-ratio -1.186689 -0.150324 -1.798208 0.185154 Skewness 0.243951 -0.049036 0.341313 0.477601 Kurtosis 4.971493 3.39366 5.199822 5.495766 Maximum loss -0.8507 -0.4355 -0.7234 -0.3546 Period of maximum loss 05/23/84 - 02/20/97 05/23/84 - 12/08/87 01/22/88 - 06/24/92 07/18/94 - 02/20/97 LIFFE N 3673 1260 1264 1147 Yearly effective return -0.073934 -0.035598 -0.198199 0.030482 Mean -0.000305 -0.000144 -0.000877 0.000119 Std. Dev. 0.014056 0.013538 0.015521 0.012851 t-ratio -1.314172 -0.377152 -2.007875 0.314005 Skewness 0.08106 -0.249777 0.353273 0.040053 Kurtosis 5.797402 5.85137 5.564294 5.721865 Maximum loss -0.8919 -0.6115 -0.7513 -0.3749 Period of maximum loss 02/05/85 - 06/24/92 02/05/85 - 12/09/87 01/19/88 - 06/24/92 08/01/94 - 02/12/97 BPDo N 3780 1303 1304 1171 Yearly effective return -0.0019 -0.028517 0.042569 -0.020163 Mean -0.000008 -0.000115 0.000165 -0.000081 t-ratio -0.070642 -0.587341 0.832657 -0.537031 Std. Dev. 0.006567 0.007056 0.007174 0.00515 Skewness -0.021897 -0.448886 0.391937 -0.086657 Kurtosis 6.133925 6.487253 4.839026 6.362086 Maximum loss -0.4748 -0.4397 -0.244 -0.1714 Period of maximum loss 02/27/85 - 09/02/92 02/27/85 - 12/31/87 06/15/89 - 09/02/92 02/15/93 - 12/31/96
Table 2.2: Autocorrelation functions of daily returns. For every data series the estimated autocorrelations are shown up to order 20. a, b, c means that the corresponding autocorrelation is significant at the 1%, 5%, 10% significance level with Bartlett (1946) standard errors. ***, **, * means that the corresponding autocorrelation is significant at the 1%, 5%, 10% significance level with Diebold (1986) heteroskedasticity-consistent standard errors.
CSCE LIFFE k 83:1-97:6 83:1-87:12 88:1-92:12 93:1-97:6 83:1-97:6 83:1-87:12 88:1-92:12 93:1-97:6 1 -0.0007 0.0328 -0.0112 -0.0277 0.0300c 0.0083 0.0456 0.0253 2 -0.0515a*** -0.0611b* -0.0524c -0.0438 -0.0378b** -0.0178 -0.0437 -0.0567c* 3 0.0038 0.0004 0.0086 -0.0036 0.0122 0.0538c* 0.0155 -0.047 4 -0.0023 -0.0007 0.0031 -0.017 0.0368b* -0.0065 0.0493c 0.0671b* 5 0.0106 -0.012 0.0141 0.0314 0.0163 0.0605b* -0.0027 -0.0048 6 -0.0192 -0.0263 0.0022 -0.0519c -0.0279c 0.0016 -0.026 -0.0704b** 7 -0.0065 -0.0155 -0.0101 0.0115 -0.0087 -0.0193 -0.036 0.0454 8 0.0062 -0.0499c 0.0255 0.0344 0.0066 -0.0068 0.0188 -0.0063 9 -0.0072 0.005 -0.0167 -0.0078 0.0217 0.0202 0.0293 0.0041 10 -0.0014 -0.0387 0.0094 0.0265 0.0398b** -0.0198 0.0662b** 0.0654b* 11 -0.024 -0.0352 -0.022 -0.0162 0.0001 -0.0012 -0.0216 0.026 12 -0.018 0.0431 -0.0613b** -0.0236 -0.0173 0.0409 -0.0649b** -0.0168 13 -0.0135 -0.0112 -0.0008 -0.046 -0.0011 0.0471c -0.0131 -0.0426 14 0.0052 0.0372 0.0005 -0.0302 0.0176 0.0002 0.0444 -0.0098 15 0.0193 0.0024 0.0437 -0.0041 0.0151 0.0357 0.0239 -0.0223 16 -0.0141 0.0049 -0.0377 0.001 0.0098 0.1279a*** -0.0775a** 0.004 17 -0.0076 0.0312 -0.0384 0.0011 -0.0193 -0.0307 -0.0257 0.0054 18 0.0156 -0.0295 0.0565b* 0.0003 0.004 -0.0209 0.0488c -0.0287 19 0.0093 -0.005 0.0135 0.0194 0.0399b** 0.0089 0.0433 0.0669b** 20 0.0135 -0.0083 0.0475c -0.0243 0.0072 -0.0306 0.0221 0.0152
BPDo k 83:1-97:6 83:1-87:12 88:1-92:12 93:1-97:6 1 0.0833a*** 0.1025a*** 0.1085a*** -0.0132 2 0.0241 0.0201 0.0165 0.0477 3 -0.0158 -0.0099 -0.0192 -0.0151 4 0.0016 -0.0313 0.0359 -0.0029 5 0.0343b* 0.0266 0.0958a*** -0.0605b 6 -0.0034 0.0286 -0.0135 -0.0411 7 -0.0303c -0.0081 -0.0598b** -0.022 8 0.0280c 0.0479c 0.025 -0.0074 9 0.0121 -0.0221 0.0357 0.0299 10 -0.0048 -0.0570b* 0.0414 0.0158 11 -0.0021 -0.0127 0.0203 -0.0246 12 -0.0203 -0.0439 -0.0068 -0.0044 13 -0.0079 -0.0087 0.0031 -0.0114 14 0.0268 0.0211 0.0386 0.0128 15 0.0305c 0.0527c 0.0478c -0.0641b* 16 -0.0009 -0.0305 0.0277 -0.0079 17 0.0131 -0.0053 0.0085 0.0487 18 -0.0341b* -0.0051 -0.0635b** -0.0059 19 -0.0131 0.0143 -0.01 -0.0366 20 0.0103 0.0232 0.0035 -0.0177
Table 2.3: Results of the best strategies applied to the CSCE cocoa futures prices. Panel A shows the results of the best five technical trading strategies applied to the CSCE cocoa futures prices for the period 1983:1-1997:6. Panel B shows the results of the best technical trading strategy in each of the three subperiods: 1983:1-1987:12, 1988:1-1992:12 and 1993:1-1997:6. The first column lists the strategy parameters. %b, td, fhp, and stl are abbreviations for the %band filter, the time delay filter, the fixed holding period and the stop-loss respectively. The second column lists the mean daily excess returns rYe on a yearly basis, that is the mean daily return times the number of trading days in a year, which is set to 252. The third column lists the mean daily excess returns of the trading rules net of 0.1% transaction costs, with the t-ratios beneath these numbers. The fourth and fifth column list the number of days classified as a buy or sell day. The number of buy and sell trades are listed beneath these numbers. The sixth and seventh column list the total number of days buy (sell) trades with a strictly positive excess return last, as a fraction of the total number of buy (sell) days. The fraction of buy and sell trades with a strictly positive excess return are listed beneath these numbers. The eight and ninth column list the mean daily return of the data series itself during buy and sell days, t-ratios are listed beneath these numbers. The last column lists the differences between the mean daily buy and sell returns and the corresponding t-ratios are listed beneath these numbers.
Panel A: Full sample, best five strategies Strategy [ %b td fhp stl] rYe re NB NS Buy>0 Sell>0 Buy Sell Buy-Sell 1983-1997 [ TRB 5 2% 50 ] 0.1038 0.00039 1450 950 0.517 0.737 0.00056 -0.00101 0.00158 1.71767 28 19 0.5 0.737 1.20175 -1.96037 2.25978 [ FR 1% 3 10 ] 0.0935 0.00036 1150 1001 0.478 0.649 0.00068 -0.00118 0.00187 1.63535 111 97 0.477 0.649 1.33110 -2.23745 2.53246 [ TRB 15 2% 50 ] 0.0832 0.00032 1000 750 0.65 0.733 0.00046 -0.00126 0.00172 1.60974 20 15 0.65 0.733 0.85819 -1.93654 2.03745 [ FR 1.5% 5 25 ] 0.0782 0.00030 1117 1050 0.62 0.69 0.00041 -0.00105 0.00146 1.37787 46 40 0.63 0.7 0.81153 -2.04345 2.02312 [ FR 8% 3 50 ] 0.0755 0.00029 1270 752 0.567 0.801 0.00034 -0.00117 0.00151 1.36795 26 16 0.577 0.813 0.71020 -1.80930 1.87465 Panel B: Subperiods, best strategy 1983-1987 [ FR 0.5% 3 50 ] 0.2016 0.00073 429 630 0.767 0.635 0.00158 -0.00057 0.00215 1.82085 9 13 0.778 0.615 1.99680 -0.94078 2.15951 1988-1992 [ MA 1, 2 25 ] 0.2156 0.00078 652 560 0.617 0.732 0.00022 -0.00221 0.00243 1.45504 21 21 0.524 0.762 0.29297 -2.76492 2.22314 1993-1997 [ FR 1% 3 10 ] 0.2105 0.00076 385 311 0.481 0.74 0.00157 -0.00145 0.00302 2.12162 38 30 0.5 0.7 2.01350 -1.66264 2.58211
Table 2.4: Results of the best strategies applied to the LIFFE cocoa futures prices. Panel A shows the results of the best five technical trading strategies applied to the LIFFE cocoa futures prices for the period 1983:1-1997:6. Panel B shows the results of the best technical trading strategy in each of the three subperiods: 1983:1-1987:12, 1988:1-1992:12 and 1993:1-1997:6.
Panel A: Full sample, best five strategies Strategy [ %b td fhp stl] rYe re NB NS Buy>0 Sell>0 Buy Sell Buy-Sell 1983-1997 [ MA 1,40 0.5% ] 0.1495 0.00055 1505 2168 0.728 0.816 0.00059 -0.00092 0.00151 2.60018 70 69 0.357 0.391 1.50434 -3.25995 3.13221 [ MA 10,75 7.5%] 0.148 0.00055 1102 1914 0.691 0.869 0.00057 -0.00104 0.00161 3.05696 33 32 0.424 0.625 1.32464 -3.59837 3.10298 [ MA 5,50 0.5% ] 0.1459 0.00054 1489 2184 0.666 0.748 0.00052 -0.00087 0.00139 2.55433 41 40 0.415 0.425 1.31265 -3.10160 2.85916 [ MA 1,30 7.5%] 0.1442 0.00053 1485 2170 0.692 0.796 0.00067 -0.00097 0.00164 2.50284 130 129 0.292 0.287 1.72202 -3.36952 3.38854 [ MA 1,30 0.1% ] 0.1422 0.00053 1510 2163 0.689 0.791 0.00063 -0.00096 0.00158 2.46005 118 117 0.297 0.308 1.61817 -3.34207 3.28657 Panel B: Subperiods, best strategy 1983-1987 [ MA 2,40 5%] 0.3547 0.00121 388 691 0.866 0.925 0.00211 -0.00146 0.00357 3.88278 19 19 0.526 0.579 2.79621 -3.19459 4.04603 1988-1992 [ FR 4% 5 50 ] 0.2517 0.00089 498 417 0.703 1 0.00078 -0.00218 0.00296 2.53028 10 9 0.7 1 1.16035 -2.72535 2.83447 1993-1997 [ FR 0.5% 2 50 ] 0.1923 0.00070 400 675 0.75 0.75 0.00128 -0.00069 0.00197 1.98085 8 13 0.75 0.769 1.92902 -1.46915 2.42358
Table 2.5: Results of the best strategies applied to the Pound-Dollar exchange rate. Panel A shows the results of the best five technical trading strategies applied to the Pound-Dollar exchange rate for the period 1983:1-1997:6. Panel B shows the results of the best technical trading strategy in each of the three subperiods: 1983:1-1987:12, 1988:1-1992:12 and 1993:1-1997:6.
Panel A: Full sample, best five strategies Strategy [ %b td fhp stl] rYe re NB NS Buy>0 Sell>0 Buy Sell Buy-Sell 1983-1997 [ TRB 100 1% 50 ] 0.0164 0.00007 215 250 0.767 0 0.00161 -0.00017 0.00178 1.93088 5 5 0.8 0 2.75658 -0.36090 2.38333 [ TRB 50 1% 50 ] 0.0127 0.00005 350 400 0.571 0 0.00097 -0.00008 0.00105 1.42095 7 8 0.571 0 2.55344 -0.20080 1.94510 [ TRB 5 1.5% 10 ] 0.0126 0.00005 160 160 0.563 0 0.00175 -0.00060 0.00235 1.68605 16 16 0.563 0 2.51482 -0.87011 2.40450 [ TRB 250 2 25 ] 0.0115 0.00005 125 125 0.6 0 0.00184 -0.00108 0.00292 1.95839 5 5 0.6 0 2.66970 -1.80209 3.19810 [ TRB 250 0.1% 25 ] 0.0115 0.00005 125 125 0.8 0 0.00184 -0.00119 0.00303 1.95916 5 5 0.8 0 2.67404 -1.95430 3.29853 Panel B: Subperiods, best strategy 1983-1987 [ MA 20,40 2%] 0.0333 0.00013 398 268 0.827 0 0.00089 -0.00040 0.00128 1.34254 12 13 0.667 0 2.79888 -0.96585 2.47666 1988-1992 [ FR 0.5% 5 25 ] 0.0534 0.00021 307 325 0.593 0 0.00141 -0.00056 0.00197 1.97336 13 13 0.615 0 3.18590 -1.56473 3.45882 1993-1997 [ MA 30,50 10 ] 0.0221 0.00009 130 130 0.615 0 0.00120 -0.00013 0.00132 1.53693 13 13 0.615 0 2.38807 -0.25821 1.88737
Table 2.6: Excess returns without transaction costs. Percentage of trading rules with a strictly positive mean excess return in the case of no transaction costs, when applied to the CSCE and LIFFE continuation series and the Pound-Dollar exchange rate, for the full sample 1983:1-1997:6 and the three subperiods 1983:1-1987:12, 1988:1-1992:12 and 1993:1-1997:6.
CSCE LIFFE BPDO Period MA TRB Filter All MA TRB Filter All MA TRB Filter All 1 16.36 18.72 33.33 19.13 80.64 75.46 69.15 77.47 12.63 14.00 3.65 12.14 2 65.94 45.56 52.74 56.90 71.77 49.22 57.21 61.78 29.57 46.36 51.41 38.32 3 15.82 19.87 36.48 19.63 36.70 36.38 42.79 37.27 2.75 3.91 3.32 3.25 Full 16.72 17.66 33.33 18.92 74.67 63.27 60.03 68.86 5.90 21.73 20.56 13.45
Table 2.7: Excess returns with 0.1% transaction costs. Percentage of trading rules with a strictly positive mean excess return in the case of 0.1% transaction costs, when applied to the CSCE and LIFFE continuation series and the Pound-Dollar exchange rate, for the full sample 1983:1-1997:6 and the three subperiods 1983:1-1987:12, 1988:1-1992:12 and 1993:1-1997:6.
CSCE LIFFE BPDo Period MA TRB Filter All MA TRB Filter All MA TRB Filter All 1 11.26 15.35 23.22 14.14 76.76 70.85 64.51 73.25 9.30 11.34 2.65 9.32 2 58.67 41.09 44.78 50.55 63.34 42.10 49.42 53.90 20.85 40.39 44.44 30.81 3 11.80 15.81 28.86 15.19 28.09 28.95 35.66 29.25 1.56 3.01 1.33 2.07 Full 9.19 12.24 25.70 12.18 64.17 52.78 49.59 58.34 2.75 18.57 16.09 10.14
Table 2.8: Significance: simple t-ratios. The table shows for all groups of trading rules (MA, TRB, Filter, All) for the full sample and for each of the three subperiods (1, 2, and 3) the percentage for which a significantly positive mean excess return occurs net of 0.1% transaction costs. The table also shows the percentage for which a significantly positive (negative) mean return during buy (sell) days occurs. Further the table shows the percentage of strategies for which the difference in mean return of the data series during buy and sell days is significantly positive. Finally the percentage of strategies for which the data series has a significantly positive mean return during buy days as well as a significantly negative mean return during sell days is given. The table only summarizes the results of one sided tests at the 10% significance level.
CSCE LIFFE BPDo Period MA TRB Filter All MA TRB Filter All MA TRB Filter All tPerf>tc 1 0.54 1.05 2.16 0.92 38.11 34.22 18.74 34.52 0.36 0.45 0.00 0.35 2 2.75 0.40 2.82 1.85 6.99 4.42 9.45 6.31 2.03 8.88 3.81 4.78 3 0.33 0.45 1.00 0.45 1.23 3.16 2.82 2.13 0.07 0.15 0.00 0.09 Full 0.22 0.10 1.33 0.30 18.31 8.38 11.44 13.86 0.07 5.22 0.83 2.07 tBuy>tc 1 1.09 1.30 1.99 1.27 25.52 30.41 19.90 26.73 16.36 9.38 4.31 12.42 2 0.07 1.05 0.66 0.50 0.65 0.50 2.32 0.78 27.72 31.76 31.01 29.63 3 0.51 0.45 3.81 0.86 2.06 7.58 5.14 4.46 0.65 0.45 0.17 0.52 Full 0.14 1.15 1.00 0.62 4.56 8.03 13.43 6.86 11.65 16.41 8.46 13.08 tSell<-tc 1 0.43 0.80 2.16 0.77 50.81 29.65 19.57 39.47 59.03 29.35 25.70 44.29 2 60.55 26.14 32.17 44.57 67.46 40.04 43.78 54.62 9.81 5.77 4.64 7.73 3 0.65 0.30 1.00 0.56 1.19 0.50 1.00 0.92 0.69 3.01 4.48 1.98 Full 6.59 3.46 10.95 5.92 64.82 36.93 29.85 50.53 19.58 15.05 12.60 17.13 tBuy-Sell>tc 1 0.98 1.30 4.15 1.46 53.85 41.60 29.85 46.65 59.54 26.24 12.44 41.90 2 1.12 1.66 6.80 1.96 8.29 4.77 18.41 8.13 27.36 25.64 21.89 26.13 3 0.80 0.75 2.49 0.97 2.68 3.76 3.15 3.14 0.72 0.80 0.83 0.77 Full 1.01 0.50 5.97 1.38 31.52 20.92 22.39 26.58 31.27 27.85 14.93 28.19 tBuy>tc Ù 1 0.07 0.00 0.00 0.04 18.64 11.99 5.47 14.70 11.91 4.92 4.15 8.44 tSell<-tc 2 0.00 0.05 0.00 0.02 0.47 0.25 1.33 0.49 5.32 3.11 1.82 4.11 3 0.00 0.00 0.17 0.02 0.07 0.20 0.33 0.15 0.00 0.20 0.00 0.07 Full 0.07 0.00 0.17 0.06 3.04 1.66 3.65 2.60 8.83 6.42 0.83 7.04
Table 2.9: Bad significance: simple t-ratios. This table shows in contrast to table 2.8 the percentage of strategies for which the mean excess return net of 0.1% transaction costs is significantly negative for all trading rules sets and for all periods. The table also shows the percentage for which a significantly negative (positive) mean return during buy (sell) days occurs. Further the table shows the percentage of strategies for which the difference in mean return of the data series during buy and sell days is significantly negative. Finally the percentage of strategies for which the data series has a significantly negative mean return during buy days as well as a significantly positive mean return during sell days is given. The table only summarizes the results of one sided tests at the 10% significance level.
CSCE LIFFE BPDo Period MA TRB Filter All MA TRB Filter All MA TRB Filter All tPerf<-tc 1 21.35 29.65 18.74 24.17 5.90 4.92 9.12 5.87 25.05 24.08 46.60 27.11 2 5.79 12.74 14.43 9.32 4.74 14.05 10.45 8.80 23.31 9.18 16.92 17.32 3 33.48 34.47 19.07 32.26 13.14 8.68 11.28 11.28 81.80 51.93 39.97 66.02 Full 29.64 41.55 26.20 33.72 5.94 7.58 13.76 7.40 80.67 40.89 48.76 62.32 tBuy<-tc 1 5.36 16.41 4.81 9.42 2.75 4.21 4.15 3.46 3.91 6.92 15.59 6.35 2 28.16 25.99 21.06 26.55 35.90 30.96 17.25 31.96 0.58 0.05 1.33 0.47 3 6.44 11.74 2.49 7.98 2.17 3.11 0.50 2.34 21.43 15.50 8.96 17.84 Full 31.81 36.83 17.74 32.13 4.56 4.21 7.79 4.76 0.72 3.01 4.15 1.96 tSell>tc 1 2.14 10.54 4.98 5.59 3.58 2.91 3.15 3.29 0.33 1.05 2.99 0.90 2 0.25 2.06 1.00 1.01 0.33 8.28 1.16 3.38 13.03 14.35 10.61 13.26 3 12.49 18.72 12.60 14.83 5.25 8.83 8.29 6.93 2.06 6.62 5.31 4.13 Full 0.76 9.03 4.15 4.22 0.80 4.47 2.16 2.32 0.72 4.16 4.15 2.39 tBuy-Sell<-tc 1 9.63 20.17 9.45 13.54 3.08 3.61 3.15 3.29 1.85 2.66 3.48 2.34 2 4.89 8.68 5.14 6.33 14.15 18.46 7.30 15.00 8.87 9.28 6.47 8.76 3 19.65 22.93 10.95 19.91 6.84 5.42 3.65 5.96 20.05 13.95 9.78 16.64 Full 9.59 25.09 7.13 15.09 2.39 2.66 4.81 2.76 1.16 3.81 2.99 2.35 tBuy<-tc Ù 1 0.47 2.61 1.49 1.38 0.87 0.80 0.66 0.82 0.11 0.05 0.50 0.13 tSell>tc 2 0.11 0.50 0.33 0.28 0.14 3.06 0.50 1.27 0.40 0.05 0.83 0.32 3 3.62 3.31 1.00 3.21 0.47 0.15 0.17 0.32 0.54 2.11 0.50 1.12 Full 0.29 3.21 0.00 1.35 0.25 0.05 0.00 0.15 0.04 2.06 0.00 0.78
Table 2.11: Significance after correction for dependence: an estimation based approach.
Panel A: This table shows for all sets of trading rules applied to the LIFFE cocoa series in the period 1983:1-1987:12 the percentage of trading rules for which the estimated coefficient of the buy (sell) dummy in the regression function of the exponential garch model is significantly positive (negative) at the 10% significance level with a one sided test (second and third column). The fourth column shows the percentage of trading rules for which the coefficient of the buy dummy is significantly positive and the coefficient of the sell dummy is significantly negative.
Rule tBuy>tc tSell<-tc tBuy>tc Ù tSell<-tc MA 40.2 32.8 29.6 TRB 41.9 22.7 16.6 Filter 38.7 17.5 9.8 All 40.6 27.4 22.8
Panel B: This table shows for all sets of trading rules applied to the LIFFE cocoa series in the period 1983:1-1987:12 the percentage of trading rules for which the estimated coefficient of the buy (sell) dummy in the regression function of the exponential garch model is significantly negative (positive) at the 10% significance level with a one sided test (second and third column). The fourth column shows the percentage of trading rules for which the coefficient of the buy dummy is significantly negative and the coefficient of the sell dummy is significantly positive.
Rule tBuy<-tc tSell>tc tBuy<-tc Ù tSell>tc MA 3.6 4.1 1.5 TRB 5.2 9.6 1.9 Filter 2.1 6.8 0.7 All 4.0 6.4 1.6
Table 2.13: Significance after correction for dependence: a bootstrap based approach.
Panel A: Bootstrap results under the null of a random walk, autoregressive, exponential garch model and a model which incorporates the structural change in the data for the LIFFE cocoa futures series in the period 1983:1-1987:12. The table lists the fractions of simulation results which are larger than the results for the original data series. The rows tPerf>tc, tBuy>tc, tSell<-tc, tBuy-Sell>tc and tBuy>tc Ù tSell<-tc show the fraction of the 500 bootstrapped time series for which the percentage of trading strategies with a significantly positive mean excess return, with a significantly positive mean buy return, with a significantly negative mean sell return, with a significantly positive mean buy-sell difference and with a significantly positive mean buy as well as a significantly negative mean sell return is larger than the same percentages when the trading strategies are applied to the original data series.
RW AR EGARCH Trend tPerf>tc 0.002 0.038 0.03 0.414 tBuy>tc 0.032 0.074 0.05 0.478 tSell<-tc 0.14 0.274 0.334 0.528 tBuy-Sell>tc 0 0.012 0.002 0.248 tBuy>tc Ù tSell<-tc 0.006 0.016 0.012 0.426
Panel B: Bootstrap results under the null of a random walk, autoregressive, exponential garch model and a model which incorporates the structural change in the data for the LIFFE cocoa futures series in the period 1983:1-1987:12. The table lists the fractions of simulation results which are larger than the results for the original data series. The rows tPerf<-tc, tBuy<-tc, tSell>tc, tBuy-Sell<-tc and tBuy<-tc Ù tSell>tc show the fraction of the 500 bootstrapped time series for which the percentage of trading strategies with a significantly negative mean excess return, with a significantly negative mean buy return, with a significantly positive mean sell return, with a significantly negative mean buy-sell difference and with a significantly negative mean buy as well as a significantly positive mean sell return is larger than the same percentages when the trading strategies are applied to the original data series.
RW AR EGARCH Trend tPerf<-tc 0.964 0.936 0.942 0.96 tBuy<-tc 0.87 0.838 0.902 0.858 tSell>tc 0.572 0.502 0.428 0.776 tBuy-Sell<-tc 0.968 0.95 0.942 0.952 tBuy<-tc Ù tSell>tc 0.342 0.274 0.278 0.542
Table 2.14: Cross-correlations. The cross-correlations between the LIFFE and CSCE continuation cocoa series, and the Pound-Dollar exchange rate for the periods 1983:1-1987:12, 1988:1-1992:12 and 1993:1-1997:6.
83:1-97:6 83:1-87:12 Corr LIFFE CSCE BPDo Corr LIFFE CSCE BPDo LIFFE 1 LIFFE 1 CSCE 0.98 1 CSCE 0.87 1 BPDO 0.66 0.51 1 BPDO 0.88 0.58 1 88:1-92:12 93:1-97:6 Corr LIFFE CSCE BPDo Corr LIFFE CSCE BPDo LIFFE 1 LIFFE 1 CSCE 0.97 1 CSCE 0.93 1 BPDO 0.08 -0.13 1 BPDO 0.26 0.16 1
Table 2.15: Excess returns when LIFFE in Dollars and CSCE in Pounds. Percentage of trading rules with a strictly positive mean excess return in the case of 0.1% transaction costs, when applied to the CSCE continuation series expressed in Pounds and the LIFFE continuation series expressed in Dollars for the full sample 1983:1-1997:6 and the three subperiods 1983:1-1987:12, 1988:1-1992:12 and 1993:1-1997:6.
CSCE in Pounds LIFFE in Dollars Period MA TRB Filter All MA TRB Filter All 1 70.03 44.66 45.77 57.93 16.61 33.32 24.54 23.71 2 34.53 27.95 34.83 32.11 77.85 55.59 51.91 66.69 3 9.70 8.38 24.05 10.84 26.75 23.78 33.50 26.40 Full 21.72 13.60 27.20 19.30 34.67 33.07 32.67 33.85
Table 2.16: Significance when LIFFE in Dollars and CSCE in Pounds: simple t-ratios. The table shows for all groups of trading rules (MA, TRB, Filter, All) for the full sample period and for each of the three subperiods (1, 2, and 3) the percentage for which a significantly positive mean excess return net of 0.1% transaction costs occurs. The table also shows the percentage for which a significantly positive (negative) mean return during buy (sell) days occurs. Further the table shows the percentage of strategies for which the difference in mean return of the data series during buy and sell days is significantly positive. Finally the percentage of strategies for which the data series has a significantly positive mean return during buy days as well as a significantly negative mean return during sell days is shown. All results reported are for the CSCE futures prices recomputed to Pounds and the LIFFE futures prices recomputed to Dollars. The table only summarizes the results of one sided tests at the 10% significance level.
CSCE in Pounds LIFFE in Dollars Period MA TRB Filter All MA TRB Filter All tPerf>tc 1 10.39 6.37 5.31 8.33 0.90 1.10 1.33 1.03 2 1.92 1.56 0.83 1.66 21.17 15.40 16.09 18.44 3 0.25 0.15 3.15 0.54 1.52 1.40 3.48 1.70 Full 0.80 0.60 1.16 0.77 1.19 0.95 2.99 1.31 tBuy>tc 1 5.21 5.92 10.95 6.13 1.38 2.16 1.66 1.70 2 0.62 0.45 1.00 0.60 0.47 3.16 4.64 1.94 3 0.36 0.40 2.82 0.65 2.79 4.62 7.96 4.05 Full 0.58 0.45 4.98 1.03 0.87 1.25 4.81 1.46 tSell<-tc 1 28.95 11.09 5.14 19.65 1.01 1.15 1.99 1.18 2 22.11 15.40 20.23 19.39 81.58 49.67 47.43 65.91 3 1.12 0.25 2.49 0.95 0.76 0.10 1.00 0.54 Full 18.57 8.43 13.60 14.25 32.18 19.47 18.74 25.97 tBuy-Sell>tc 1 26.71 11.89 10.61 19.41 1.88 2.21 2.99 2.13 2 2.97 2.26 5.97 3.05 14.95 12.09 23.05 14.81 3 0.76 0.25 5.14 1.06 2.28 2.06 5.64 2.58 Full 2.82 1.51 6.30 2.73 5.50 3.11 9.78 5.10 tBuy>tc Ù 1 0.90 0.20 0.17 0.56 0.14 0.00 0.33 0.11 tSell<-tc 2 0.11 0.05 0.00 0.07 0.07 1.86 0.83 0.82 3 0.04 0.00 0.50 0.07 0.18 0.00 0.66 0.17 Full 0.11 0.05 0.17 0.09 0.22 0.25 1.16 0.34
Table 2.17: Bad significance when LIFFE in Dollars and CSCE in Pounds: simple t-ratios. This table shows in contrast to table 2.16 the percentage of strategies for which the mean excess return net of 0.1% transaction costs is significantly negative for all trading rules sets and all periods. The table also shows the percentage for which a significantly negative (positive) mean return during buy (sell) days occurs. Further the table shows the percentage of strategies for which the difference in mean return of the data series during buy and sell days is significantly negative. Finally the percentage of strategies for which the data series has a significantly negative mean return during buy days as well as a significantly positive mean return during sell days is shown. All results reported are for the CSCE futures prices recomputed to Pounds and the LIFFE futures prices recomputed to Dollars. The table only summarizes the results of one sided tests at the 10% significance level.
CSCE in Pounds LIFFE in Dollars Period MA TRB Filter All MA TRB Filter All tPerf<-tc 1 6.01 9.23 13.60 8.07 14.66 8.83 13.43 12.37 2 11.07 13.45 20.23 12.96 3.08 7.53 14.10 5.94 3 30.84 39.14 16.09 32.30 13.68 16.86 13.76 14.89 Full 13.46 28.70 24.71 20.42 8.61 10.59 20.90 10.74 tBuy<-tc 1 3.18 5.22 4.64 4.11 1.38 4.62 1.82 2.63 2 36.12 24.89 23.38 30.51 26.06 21.78 25.21 24.36 3 9.48 15.96 3.48 11.23 1.34 1.71 0.66 1.40 Full 13.54 22.98 15.09 17.24 7.82 7.23 13.60 8.26 tSell>tc 1 2.46 5.47 6.30 4.02 1.70 1.76 3.32 1.91 2 0.54 7.43 1.82 3.25 0.25 3.31 0.66 1.44 3 3.98 11.74 9.45 7.49 9.70 19.92 16.92 14.33 Full 1.16 4.67 4.98 2.90 0.40 3.66 2.16 1.81 tBuy-Sell<-tc 1 3.66 5.67 4.48 4.50 5.36 3.51 5.64 4.71 2 16.58 10.89 9.78 13.71 4.42 5.17 7.96 5.10 3 17.41 26.84 8.46 19.93 7.09 9.48 8.13 8.11 Full 5.79 13.60 10.12 9.19 1.81 2.81 5.47 2.60 tBuy<-tc Ù 1 0.58 0.70 0.50 0.62 0.25 0.20 0.17 0.22 tSell>tc 2 0.14 0.40 0.33 0.26 0.04 0.05 0.00 0.04 3 2.28 5.17 1.82 3.31 0.22 0.25 0.50 0.26 Full 0.40 0.75 0.83 0.58 0.07 0.05 0.33 0.09
B. Parameters of technical trading strategies
This appendix presents the values of the parameters of the technical trading strategy set applied in this chapter. Most parameter values are equal to those used by Sullivan et al. (1999). Each basic trading strategy can be extended by a %-band filter (band), time delay filter (delay), fixed holding period (fhp) and a stop-loss (sl). The total set consists of 5353 different trading rules, including the strategies that are always short, neutral or long.Moving-average rules
| n | =number of days over which the price must be averaged |
| band | =%-band filter |
| delay | =number of days a signal must hold if you implement a time delay filter |
| fhp | =number of days a position is held, ignoring all other signals during this period |
| sl | =%-rise (%-fall) from a previous low (high) to liquidate a short (long) position |
| n | =[1, 2, 5, 10, 15, 20, 25, 30, 40, 50, 75, 100, 125, 150, 200, 250] |
| band | =[0.001, 0.005, 0.01, 0.015, 0.02, 0.03, 0.04, 0.05] |
| delay | =[2, 3, 4, 5] |
| fhp | =[5, 10, 25, 50] |
| sl | =[0.02, 0.03, 0.04, 0.05, 0.075, 0.10] |
With the 16 values of n we can construct ( 216)=120 basic moving-average (MA) trading strategies. We extend these strategies with %-band filters, time delay filters, fixed holding period and a stop-loss. The values chosen above will give us in total:
120+120*8+120*4+120*4+120*6=2760 MA strategies.
Trading range break-out rules
| n | = length of the period to find local minima (support) and maxima (resistance) |
| band | =%-band filter |
| delay | =number of days a signal must hold if you implement a time delay filter |
| fhp | =number of days a position is held, ignoring all other signals during this period |
| sl | =%-rise (%-fall) from a previous low (high) to liquidate a short (long) position |
| n | =[5, 10, 15, 20, 25, 50 ,100, 150, 200, 250] |
| band | =[0.001, 0.005, 0.01, 0.015, 0.02, 0.03, 0.04, 0.05] |
| delay | =[2, 3, 4, 5] |
| fhp | =[5, 10, 25, 50] |
| sl | =[0.02, 0.03, 0.04, 0.05, 0.075, 0.10] |
With the parameters and values given above we construct the following trading range break-out (TRB) strategies:
| basic TRB strategies: | 10*1 | =10 |
| TRB with %-band filter: | 10*8 | =80 |
| TRB with time delay filter: | 10*4 | =40 |
| TRB with fixed holding period: | 10*4 | =40 |
| TRB with stop-loss: | 10*6 | =60 |
| TRB with %-band and time delay filter: | 10*8*4 | =320 |
| TRB with %-band and fixed holding: | 10*8*4 | =320 |
| TRB with %-band and stop-loss: | 10*8*6 | =480 |
| TRB with time delay and fixed holding: | 10*4*4 | =160 |
| TRB with time delay and stop-loss: | 10*4*6 | =240 |
| TRB with fixed holding and stop-loss: | 10*4*6 | =240 |
This will give in total 1990 TRB strategies.
Filter rules
| filt | = %-rise (%-fall) from a previous low (high) to generate a buy (sell) signal |
| delay | =number of days a signal must hold if you implement a time delay filter |
| fhp | =number of days a position is held, ignoring all other signals during this period |
| filt | =[0.005, 0.01, 0.015, 0.02, 0.025, 0.03, 0.035, 0.04, 0.045, 0.05, |
| 0.06, 0.07, 0.08, 0.09, 0.1, 0.12, 0.14, 0.16, 0.18, 0.2, 0.25, | |
| 0.3, 0.4, 0.5] | |
| delay | =[2, 3, 4, 5] |
| fhp | =[5, 10, 25, 50] |
With the parameters and values given above we construct the following filter rules (FR):
| basic FR: | 24*1 | =24 |
| FR with time delay: | 24*4 | =96 |
| FR with fixed holding: | 24*4 | =96 |
| FR with time delay and fixed holding: | 24*4*4 | =384 |
This will give in total 600 filter rules.
- 1
- Contract specifications of January 26, 1998.
- 2
- We thank the cocoa-trading firm Unicom International B.V. and ADP Financial Information Services for providing the data.
- 3
- The pasting date is equal to the roll over date.
- 4
- H0: sr(csce)2=sr(liffe)2 vs H1: sr(csce)2 ¹ sr(liffe)2; F=Sr(csce)2/Sr(liffe)2;
- 5
- Because sample autocorrelation may be spurious in the presence of heteroskedasticity we also tested for significance by computing Diebold (1986) heteroskedasticity-consistent estimates of the standard errors, se(k)=1/n (1+g(r2, k)/s4), where n is the number of observations, g(r2, k) is the k-th order sample autocovariance of the squared returns, and s is the standard error of the returns. ***, **, * in table 2.2 then indicates whether the corresponding autocorrelation is significantly different from zero.
- 6
- Positions are unchanged until the moving averages really cross.
- 7
- In practice traders can hold a margin of 10% of the underlying value. The broker issues frequently a margin call, that is to add money to the margin, if the trader is in a losing position. However, to keep things as simple as possible we assume a fully protected trading position by setting the required margin to 100% of the underlying value.
- 8
- Nelson (1991) replaces the normal distribution used here with a generalized error distribution.
- 9
- We checked for significance of the estimated coefficients. We did diagnostic checking on the standardized residuals, to check whether there was still dependence. We used the (partial) autocorrelation function, Ljung-Box (1978) Q-statistics and the Breusch-Godfrey LM-test. The Schwartz Bayesian criterion was used for model selection.
- 10
- This model is found to fit the data the best, see page ??.
- 11
- We would like to thank Guido Veenstra, employed at the Dutch cocoa firm Unicom, for pointing this out to us.



Home | Contents | Chapter 1 | Chapter 2 | Chapter 3 | Chapter 4 | Chapter 5 | Chapter 6 | References
Copyright © 2004 Gerwin Griffioen