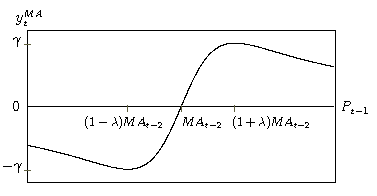Gerwin Griffioen's Technical Analysis Pages

Griffioen, G.A.W. (2003), "Technical Analysis in Financial Markets", PhD thesis, University of Amsterdam.

Chapter 6
An Evolutionary Adaptive Learning Model with Fundamentalists and Moving Average Traders

6.1 Introduction

Chapters 2 through 5 of this thesis contain empirical analyses whether technical trading has statistically significant forecasting power and yields economically significant profits when applied to financial time series. The present chapter builds a simple theoretical financial market model with fundamentalists and technical analysts.

An important question in heterogeneous agents modeling is whether irrational traders can survive in the market, or whether they would lose money and are driven out of the market by rational investors, who would trade against them and drive prices back to fundamentals, as argued by e.g. Friedman (1953). In the last decade a number of theoretical and/or computational heterogeneous agent models, with fundamentalist traders competing against technical analysts, have been developed, see e.g. in Frankel and Froot (1988), De Long et al. (1989, 1990), Kirman (1991), Wang (1994), Lux (1995), Arthur et al. (1997), Brock and Hommes (1997, 1998), Farmer (1998), Hong and Stein (1999) and LeBaron et al. (1999). A common feature of these contributions is that technical traders may at times earn positive profits, survive evolutionary competition and need not be driven out of the market by trading strategies based upon economic fundamentals.

Brock and Hommes (1998) investigate the dynamical behavior of a simple financial market model with heterogeneous adaptively learning traders, where the fraction of traders following a certain forecasting rule changes over time. The traders are restricted to choose from a finite set of fundamental and trend following trading techniques. How many traders are using a particular technique in predicting prices depends on the past performances of these techniques, as measured by past profits or forecasting accuracy. Emphasis is placed on the change in dynamical behavior when the intensity of choice parameter, measuring how quickly agents switch between forecasting techniques, is varied. It is found that increasing this intensity of choice can lead to market instability and the emergence of complicated dynamics for asset prices and returns, with irregular switching between phases where prices are near to the fundamental value and phases of optimism where traders extrapolate trends. An extremely rich asset price dynamics emerges, with bifurcation routes to strange attractors, especially if switching to more successful strategies becomes more rapid. It is also found that even when costs of information gathering and trading are zero, then fundamentalists are in general not able to drive other trader types out of the market. Thus it is concluded that simple technical trading rules may survive evolutionary competition in a heterogeneous world where prices and beliefs coevolve over time and that therefore the Friedman argument should be considered with care. See e.g. Hommes (2001) for a survey and an extensive discussion of these points.

One of the goals of heterogeneous agents modeling is to develop simple financial asset pricing models that mimic the well-known characteristics of real financial return distributions, such as little autocorrelation in the returns, volatility clustering and fat tails. Gaunersdorfer and Hommes (2000) develop a model in which volatility clustering becomes an endogenous phenomenon by the interaction of heterogeneous agents. Volatility clustering is caused by the coexistence of attractors, a stable fundamental steady state and a stable (quasi) periodic cycle. The time series properties of the model are compared with the daily closing prices of the S&P 500 in the period August 1961 through May 2000 and furthermore a GARCH model is estimated. It is concluded that the model approximates reality fairly well.

This chapter is an extension of the Brock and Hommes (1998) model in that it adds a real moving-average technical trading strategy to the set of beliefs the traders can choose from. Moving averages are well known and frequently used prediction rules in financial practice. They are intended to smooth out an otherwise volatile time series and to show its underlying directional trend. Furthermore, the model proposed in this chapter assumes that traders have constant relative risk aversion. That is, every trader in a given belief group invests the same proportion of his individual wealth in the risky asset. Hence, traders take the same amount of risk relative to their wealth. In the Brock and Hommes (1998) model, in contrast, it is assumed that the traders have constant absolute risk aversion. Irrespective of their individual wealth every trader in a certain belief group will buy or sell short the same amount of stocks. Thus traders with less wealth are prepared to take greater relative risks than traders with more wealth. It should be noted that in the case of zero supply of outside stocks, the model developed in this chapter reduces to the Brock and Hommes (1998) model.

In nonlinear dynamical models it is in general impossible to obtain explicit analytic expressions for the periodic and chaotic solutions. Therefore in applied nonlinear dynamics it is common practice to use a mixture of theoretical and numerical methods to analyze the dynamics. We perform a bifurcation analysis of the steady state by using numerical tools, such as delay and phase diagrams, bifurcation diagrams and the computation of Lyapunov exponents. In particular we show analytically that the fundamental steady state may become unstable due to a Hopf bifurcation.

In section 6.2 the Brock and Hommes (1998) financial market model with adaptively learning agents is reviewed. Thereafter, in section 6.3, the heterogeneous agents model with fundamentalists versus moving average traders, resulting in an eight dimensional nonlinear dynamical system, is derived. In section 6.4 a procedure is developed to determine trading volume. Section 6.5 presents an analytical stability analysis of the fundamental steady state. The eigenvalues of the linearized system are computed and it is examined which kind of bifurcations can occur. In section 6.6 numerical simulations are used to study the dynamical behavior of the model, especially when the steady state is locally unstable. Finally section 6.7 summarizes and concludes.

6.2 The Brock-Hommes heterogeneous agents model

In this section we discuss the discounted value asset pricing model with heterogeneous beliefs of Brock and Hommes (1998)¹. Consider a market with N agents who can select independently from each other a strategy h from a finite set of H different beliefs or forecasting rules to base trading decisions upon. Agents have to make a capital allocation decision between a risky asset P and a risk free asset F. There are no restrictions on the amount of money which can be borrowed or lend and there are also no restrictions on the number of shares that can be bought or sold short. Agent j can choose to buy or sell short z_j,t shares of the risky asset at time t. The wealth of agent j at time t+1 is then equal to

W_j,t+1=R W_j,t + z_j,t (P_t+1+D_t+1-RP_t), (1)

where R=(1+r^F) is the risk free gross return, r^F is the risk free net return assumed to be constant, P_t is the equilibrium price of the risky asset at time t and D_t is the dividend paid at time t. The term (P_t+1+D_t+1-R P_t) is equal to the excess profit of one long position in the risky asset.

BH make the following assumptions regarding the trading process. All agents are price takers. That is, an agent cannot influence the market's equilibrium price by his individual investment decision. The demand for the risky asset z_j,t is a continuous monotonically decreasing function of the price P_t at time t. Further, the model follows a Walrasian equilibrium price scenario. Before the setting of the equilibrium price at time t, each agent j chooses a trading strategy h and makes an optimal investment decision z_j,t^h in the time interval (t-1, t). Expectations about future prices and dividends are made on the basis of the information set of past equilibrium prices and dividends {P_t-i, D_t-i: i ł 1 } (note that P_t and D_t are not included). Through the market mechanism an equilibrium price is set so that the market clears. Dividends D_t paid at time t can immediately be reinvested at time t.

Demand

BH define the information set I_t={P_t-i, D_t-i: i ł 1 } Č {P_t, D_t}, where {P_t-i: i ł 1 } are past equilibrium prices, {D_t-i: i ł 1 } are past dividends, {D_t} is current dividend, but where {P_t} is not yet necessarily the equilibrium price. The conditional expected wealth of agent j at time t who invests according to strategy h is then equal to

E_j^h(W_j,t+1|I_t)=E_j,t^h(W_j,t+1)=RW_j,t + z_j,t^h E_t^h(P_t+1+D_t+1-RP_t), (2)

where E_t^h(P_t+1+D_t+1-RP_t) is the forecast strategy h makes about the excess profit of the risky asset at time t+1 conditioned on I_t. The agent also makes a forecast about the dispersion of his expected wealth conditioned on I_t

V_j^h(W_j,t+1|I_t)=V_j,t^h(W_j,t+1)=(z_j,t^h)² V_t^h(P_t+1+D_t+1), (3)

where V_t^h(P_t+1+D_t+1) is the forecast of belief h about the dispersion of expected price plus dividend. It is assumed that if the conditional expected excess profit of belief h is positive, then the agent holds a long position in the market (z_j,t^h ł 0) and if the conditional expected excess profit is strictly negative, then the agent holds a short position in the market (z_j,t^h<0), so that conditional expected wealth is always equal or larger than RW_j,t.

Solving the conditional variance equation (6.3) for z_j,t^h yields

z_j,t^h=±

V_j,t^h(W_j,t+1)

V_t^h(P_t+1+D_t+1)

, (4)

where the ± sign depends on the sign of the expected excess profit on the risky asset by belief h. The capital allocation line (CAL) of agent j with belief h is derived by substituting (6.4) in the conditional expectations equation (6.2) which yields

E_j,t^h(W_j,t+1)=RW_j,t + S_t^h V_j,t^h(W_j,t+1) if E_t^h(P_t+1+D_t+1-RP_t)ł 0; (5)

E_j,t^h(W_j,t+1)=RW_j,t - S_t^hV_j,t^h(W_j,t+1) if E_t^h(P_t+1+D_t+1-RP_t)<0; (6)

S_t^h=

E_t^h(P_t+1+D_t+1-RP_t)

V_t^h(P_t+1+D_t+1)

E_t^h(P_t+1+D_t+1-RP_t)/P_t

V_t^h(P_t+1+D_t+1)/P_t²

E_t^h(r_t+1^P-r^f)

V_t^h(r_t+1^P)

Here r_t+1^P is the return of the risky asset at time t+1 and |S_t^h| is the reward to variability ratio, or stated differently, the extra expected return to be gained per extra point of expected risk to be taken. The CAL shows the relation between the expected wealth and the expected dispersion of the wealth by agent j. The CAL is always an increasing function of V_j,t^h(W_j,t+1), which means that the more risk the agent expects to take, the more he expects to earn.

BH assume that each agent has constant absolute risk aversion (CARA) and that the utility of the asset allocation decision of agent j who invests according to belief h at time t is given by

U_j,t^h=E_j,t^h(W_j,t+1)-

a_j

V_j,t^h(W_j,t+1), (7)

where a_j is the risk aversion parameter of agent j. Every agent chooses an asset allocation that maximizes his utility, that is

Max_{z_j,t^h} E_j,t^h(W_j,t+1)-

a_j

V_j,t^h(W_j,t+1) under the CAL (6.5) or (6.6). (8)

This maximization yields the optimal choice of the number of stocks to be bought or sold short

z_j,t^h(P_t)=

E_t^h(P_t+1+D_t+1-RP_t)

a_j V_t^h(P_t+1+D_t+1)

, (9)

where z_j,t^h(P_t) Î IR is the demand for shares as a continuous monotonically decreasing function of P_t. If z_j,t^h>0, then a long position in the market is taken and if z_j,t^h<0, then a short position in the market is taken. If it is assumed that all agents have the same risk aversion parameter a_j=a, then all agents with the same belief buy or sell short the same number of shares irrespective of their wealth. If j Î belief h, then z_j,t=z_j,t^h=z_t^h, where z_t^h is the number of shares recommended to be bought or sold short by belief h at time t.

Market equilibrium

Equilibrium of demand and supply yields

j=1

z_j,t=

h=1

ć
ç
ç
č

{j Î belief h}

z_j,t^h

ö
÷
÷
ř

= S, (10)

where S is the total number of shares available in the market. Hence in equilibrium the total number of shares demanded by the agents should be equal to the total number of shares available. Equilibrium equation (6.10) can be rewritten as

h=1

N_t^h z_t^h=S, (11)

where N_t^h is the number of agents having belief h at time t. If both sides of equation (6.11) are divided by the total number of agents N trading in the market, then

h=1

n_t^h z_t^h=s, (12)

where n_t^h=N_t^h/N is the fraction of agents with belief h and s=S/N is the number of shares available per agent.

Further, BH assume that the conditional variance V_t^h(P_t+1+D_t+1)=s² is constant through time and equal for all beliefs. This assumption of homogeneous, constant beliefs on variance is made primarily for analytical tractability. Notice however that heterogeneity in conditional expectations in fact leads to heterogeneity in conditional variance as well, but this second-order effect will be ignored. Equilibrium equation (6.12) can be solved for P_t to yield the equilibrium price

P_t=

h=1

{

n_t^h E_t^h(P_t+1+D_t+1)

}

a s² s. (13)

If the number of outside shares per trader is zero, i.e. if s=0, then the equilibrium price at time t is equal to the net present value of the average expected price plus dividends at time t+1.

Evolutionary dynamics

The fraction of agents who choose to invest according to belief or forecasting rule h are determined by a discrete choice model. Every agent chooses the belief with the highest fitness he observes. Individually observed fitness is derived from a random utility model and given by:

F_j,t^h=F_j,t^h+e_j,t^h, (14)

where F_j,t^h is the deterministic part of the fitness measure and e_j,t^h represents personal observational noise. If e_j,t^h ą 0, then this model means that agent j cannot observe the true fitness F_{j, t}^h of belief h perfectly, but only with some observational noise. Assuming that the noise e_j,t^h is iid drawn across beliefs h=1,...,H and across agents j=1,...,N from a double exponential distribution, then the probability that agent j chooses belief h is equal to

q_j,t^h=

exp(b_j F_{j, t-1}^h)

k=1

exp(b_j F_{j, t-1}^k)

. (15)

Here b_j is called the intensity of choice, measuring how sensitive agent j is to selecting the optimal belief. The intensity of choice b_j is inversely related to the variance of the noise terms e_j,t^h. If agent j can perfectly observe the fitness of each belief in each period, then V(e_j,t^h) Ż 0 and b_j ® Ą and the agent chooses the best belief with probability 1. If agent j cannot observe differences in fitness, then V(e_j,t^h)® Ą and b_j Ż 0 and the agent chooses each belief with equal probability 1/H.

The excess profit of an agent following strategy h in period t is equal to (P_t+D_t-R P_t-1) z_t-1^h. Therefore the fitness measure of strategy type h as observed by agent j is defined as

F_{j, t}^h=(P_t+D_t-R P_t-1)z_t-1^h-C_j^h+h_j F_{j, t-1}^h.

Here 0 Ł h_j Ł 1 is the personal memory parameter and C_j^h is the average per period cost of obtaining forecasting strategy h for agent j. If h_j=1, the memory of the agent is infinite and F_j,t^h is equal to the cumulative excess profits of belief h until time t. In this case F_{j, t}^h measures the total excess profit of the belief from the beginning of the process. If h_j=0, the agent has no memory and F_{j, t}^h is equal to the excess profit on time t-1. If 0 < h_j < 1, then F_j,t^h is a weighted average of past excess profits with exponentially declining weights. The higher the costs C_j^h, the more costly it is for the agent to obtain and invest according to belief h, and the more unlikely it will be that the agent chooses belief h.

BH assume that b_j=b, h_j=h and C_j^h=C^h for all agents, so that F_j,t^h=F_t^h and q_j,t^h=q_t^h are equal for all agents. This means that all agents have the same intensity of choice, have the same memory and face the same costs for trading. Under this assumption, in the limit, as the number of agents goes to infinity, the fraction of agents who choose to invest according to belief h converges in probability to q_t^h. Thus in the equilibrium price equation (6.13) n_t^h can be replaced by q_t^h. Furthermore, it is assumed that all agents have the same risk aversion parameter a_j=a, so that agents who follow the same forecasting rule have the same demand. Hence, in the end, in the heterogeneous agents model of Brock and Hommes (1998), the agents are only heterogeneous in the beliefs they can choose from.

6.3 A modified heterogeneous agents
asset pricing model

6.3.1 Utility-maximizing beliefs

As in the BH model we consider a market with N agents who can select independently from each other a strategy h from a finite set of H different beliefs or forecasting rules to base trading decisions upon. Agents have to make a capital allocation decision between a risky asset P and a risk free asset F. Agent j can choose to invest at time t a fraction y_j,t of his wealth W_j,t in the risky asset P and a fraction 1-y_j,t in the risk free asset F. If P_t is the price of the risky asset at time t and D_t is the dividend paid at time t, then the net return of the risky asset at time t+1 is defined as r_t+1^P=(P_t+1+D_t+1-P_t)/P_t and the net risk free return is denoted by r^F and is assumed to be constant. The net return of the agent's j complete portfolio C at time t+1 is then equal to

r_j,t+1^c=(1-y_j,t) r^F+y_j,t r_t+1^P=r^F+y_j,t (r_t+1^P-r^F),

where r_t+1^P-r^F is the excess return on the risky asset. In this section we derive the demand function for the risky asset if the agent has constant relative risk aversion and determines his optimal demand for the risky asset by maximizing his mean-variance utility curve on his capital allocation line. The demand function is derived under the assumption that the agent makes price predictions. In subsection 6.3.2 we present the demand function for the risky asset if the agent does not make price predictions, but only chooses to buy or sell short the asset on the basis of a technical trading strategy.

We make the following assumptions regarding the trading process. All agents are price takers. That is, an agent cannot influence the market's equilibrium price by his individual investment decision. Further, the model follows a Walrasian equilibrium price scenario. Each agent j chooses a strategy h and makes an optimal investment decision y_j,t^h in the time interval (t-1, t), before the setting of the equilibrium price at time t. Expectations about future prices and dividends are made on the basis of the information set of past equilibrium prices and dividends {P_t-i, D_t-i: i ł 1 } (note that P_t and D_t are not included). Through the market mechanism an equilibrium price is set so that the market clears. Dividends D_t paid at time t can immediately be reinvested at time t.

We define the information set I_t={P_t-i, D_t-i: i ł 1 } Č {P_t, D_t}, where {P_t-i: i ł 1 } are past equilibrium prices, {D_t-i: i ł 1 } are past dividends, {D_t} is current dividend, but where {P_t} is not yet necessarily the equilibrium price. The conditional expected portfolio return of agent j at time t who invests according to strategy h is then equal to

E_j^h(r_j,t+1^c|I_t)=E_j,t^h(r_j,t+1^c)=r^F+y_j,t^h E_t^h(r_t+1^P-r^F), (16)

where E_t^h(r_t+1^P-r^F) is the forecast belief h makes about the excess return of the risky asset at time t+1 conditioned on I_t. If the conditional expected excess return of belief h is positive, then the fraction invested in the risky asset is positive (y_j,t^h ł 0) and if the conditional expected excess return is strictly negative, then the fraction invested in the risky asset is strictly negative (y_j,t^h<0). Hence agent j with belief h can choose to buy shares or to sell shares short. Agent j does not only forecast his portfolio return but also the dispersion of the portfolio return which is equal to

V_j^h(r_j,t+1^c|I_t)=V_j,t^h(r_j,t+1^c)=(y_j,t^h)² V_t^h(r_t+1^P), (17)

where V_t^h(r_t+1^P) is the forecast of belief h about the dispersion of the excess return of the risky asset. Solving (6.17) for y_j,t^h yields

y_j,t^h=±

V_j,t^h(r_t+1^c)

V_t^h(r_t+1^P)

if V_t^h(r_t+1^P)>0, (18)

where the ± sign depends on the conditional expected excess return of the risky asset. The capital allocation line (CAL) can be derived by substituting (6.18) in the conditional expectations equation (6.16), that is

E_j,t^h(r_j,t+1^c)=r^F + S_t^h V_j,t^h(r_j,t+1^c) if E_t^h(r_t+1^P-r^F)ł 0; (19)

E_j,t^h(r_j,t+1^c)=r^F - S_t^h V_j,t^h(r_j,t+1^c) if E_t^h(r_t+1^P-r^F)<0; (20)

S_t^h=

E_t^h(r_t+1^P-r^F)

V_t^h(r_t+1^P)

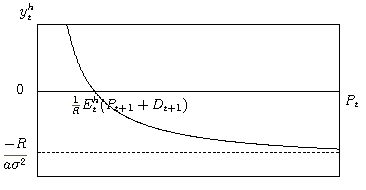
Here |S_t^h| is the reward to variability ratio, or stated differently, the extra expected return to be gained per extra point of expected risk to be taken. The CAL shows the relation between the expected return and the expected dispersion of the return. The CAL is always an increasing function of V_j,t^h(r_j,t+1^c). This implies that the more risk the agent expects to take, the more he expects to earn.

We assume that the agents have a constant relative risk aversion so that the utility of the capital allocation decision by agent j with belief h is given by

U_j,t^h=E_j,t^h(r_j,t+1^c)-

a_j

V_j,t+1^h(r_j,t^c), (21)

where a_j is the risk aversion parameter of agent j. Every agent chooses an asset allocation that maximizes his utility

Max_{y_j,t^h} E_j,t^h(r_j,t+1^c)-

a_j

V_j,t^h(r_j,t+1^c) under CAL (6.19) or (6.20). (22)

The first order condition of (6.22) is

d U_j,t^h

d y_j,t^h

=E_t^h(r_t+1^P-r^F) - a_j y_j,t^h V_t^h(r_t+1^P)=0.

This implies that the optimal fraction of individual wealth invested in the risky asset by agent j with belief h as function of the price P_t is equal to

y_j,t^h(P_t)=

E_t^h(r_t+1^P-r^F)

a_j V_t^h(r_t+1^P)

. (23)

Since the second order condition

d² U_j,t^h

d (y_j,t^h)²

=-a_j V_t^h(r_t+1^P)<0

is satisfied, utility is maximized. If y_j,t^h>0, then a long position in the risky asset is held. If y_j,t^h<0, then a short position in the risky asset is held. If we assume that all agents have the same risk aversion parameter a_j=a, then all agents with the same belief h invest the same fraction of their individual wealth in the risky asset. If agent j has belief h, then y_j,t=y_j,t^h=y_t^h, where y_t^h is the optimal fraction of wealth invested in the risky asset at time t recommended by belief h. Under the assumption that a_j=a it is also true that U_j,t^h=U_t^h for all j. Further we assume that the conditional variance V_t^h(r_t+1^P)=s² is constant through time and equal for all beliefs. y_t^h(P_t) can now be rewritten as:

y_t^h(P_t)=

P_t

E_t^h(P_t+1+D_t+1)-R

a s²

(24)

which is a convex monotonically decreasing function of P_t. Note that we can bring P_t outside the expectations formula, because the price is not a random variable, but an equilibrium price set by the market auctioneer. Stated differently, the fraction of wealth invested in the risky asset at time t depends on the price set by the market at time t and the forecast or belief about the price at time t+1, based on all available information until time t but not including P_t. Figure 6.1 illustrates the demand function of the mean-variance utility maximizing belief.

Figure 6.1: Demand function of the mean-variance utility maximizing belief

6.3.2 Non-utility-maximizing beliefs: technical traders

In subsection 6.3.1 we have derived the demand function for the risky asset under the assumptions that agents make price predictions and maximize a constant relative risk aversion utility function on a capital allocation line. However, if investors use technical trading rules, then they often do not try to make a point forecast of the price directly, but they make an investment decision based on the direction of a trend in prices. Pring (1992) defines technical analysis as the art of detecting a price trend in an early stage and maintaining a market position until there is enough weight of evidence that the trend has reversed. Thus, if we want to model technical traders, then we must define a demand function for the risky asset in another way as we did in section 6.3.1.

We take as an example the exponential moving-average trading rule. The advantage of this rule over the usual equally weighted moving-average trading rule is that it keeps the dimension of our model low. Demand functions for other technical trading rules can be derived according to the same concept. The exponential moving average at time t is equal to

MA_t=µ P_t + (1-µ) MA_t-1=µ

t-1

j=0

(1-µ)^j P_t-j + (1-µ)^t MA₀, (25)

where 0 < µ < 1. In this formula more recent prices get a higher weight than prices further into the past. The advantage of moving-average rules is that they follow the trend, are easy to compute and smooth an otherwise volatile series. The smaller µ, the more the moving average smoothes the price series, or stated differently, the more the moving average follows the price series at a distance. A small µ places little weight on current price and can be used to detect long term trends, while a large µ places large weight on current price and can be used to detect short term trends.

Trading signals are generated by the crossing of the price through the moving average. If the price crosses the moving average upwards, i.e. P_t>MA_t Ů P_t-1Ł MA_t-1, then a buy signal is generated and at time t+1 a long position in the market is taken. If the price crosses the moving average downwards, i.e. P_t<MA_t Ů P_t-1ł MA_t-1, then a sell signal is generated and at time t+1 a short position in the market is taken. The magnitude of the position held in the market can also be conditioned on the distance between the price and the moving average. If P_t is close to MA_t, small positions should be held, because it is uncertain whether the strategy generated correct signals. It also seems reasonable to assume that if P_t is very far away from MA_t, then small positions should be held, because the price exploded too fast away from MA_t.

To satisfy above conditions the demand of the moving average forecasting rule, as a fraction of individual wealth at time t, y_t^MA, is defined as a continuous function of past prices and moving averages in the following way:

x_t-1=

l (1-µ)

P_t-1-MA_t-1

MA_t-2

P_t-1-MA_t-2

MA_t-2

;

y_t^MA=f(x_t-1)=2 g

x_t-1

1+x_t-1²

(26)

where l>0, g>0. Notice that in contrast to the fraction y_t^h(P_t) in (6.24), the fraction y_t^MA of wealth invested by moving average traders in the risky asset does not depend upon the (unknown) market equilibrium price P_t, but only upon past price observations and moving averages.

The demand function (6.26) has the following properties (see figure 6.2 for illustration):

0cm y_t^MA<0 if P_t-1<MA_t-1
y_t^MA=0 if P_t-1=MA_t-1
y_t^MA>0 if P_t-1>MA_t-1
lim_{P_t-1® Ą} y_t^MA=0
lim_{P_t-1Ż 0} y_t^MA=-2 g l/1+l²
d y_t^MA/d P_t-1= 2 g (1/l MA_t-2) 1-x²/(1+x²)²
minimum: (P_t-1, y_t^MA)=((1-l)MA_t-2, -g)
maximum: (P_t-1, y_t^MA)=((1+l)MA_t-2, g)

The parameter g controls for the maximum and minimum fraction of wealth the technical trader can invest in the risky asset. The parameter l controls for the location of the extrema. Within some band around the moving average, which depends on the value of l, y_t^MA increases (or decreases) to a maximum (or minimum) value g (or -g). Outside this band the further away price deviates from the moving average, the more y_t^MA decreases in absolute value.

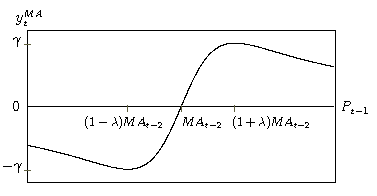
Figure 6.2: Demand function exponential moving average belief

6.3.3 Market equilibrium

Wealth per agent, total wealth and market clearing

The number of shares agent j who follows belief h holds in the risky asset at time t depends on his individual wealth and the equilibrium price, that is

z_j,t^h=

y_t^h W_j,t

P_t

. (27)

Here W_j,t is the wealth of agent j at time t, which depends on the fraction of the wealth invested at time t-1, that is

W_j,t=

(

1+r^F+y_j,t-1 (r_t^P-r^F)

)

W_j,t-1=

ć
ç
ç
č

1+r^F+y_j,t-1

ć
ç
ç
č

P_t+D_t

P_t-1

-(1+r^F)

ö
÷
÷
ř

W_j,t-1=

R W_j,t-1 +

(

P_t+D_t-R P_t-1

)

y_j,t-1 W_j,t-1

P_t-1

R W_j,t-1 +

(

P_t+D_t-R P_t-1

)

z_j,t-1.

(28)

The total wealth of all N agents at time t is equal to

W_t=

j=1

W_j,t=

j=1

W_j,t-1 + (P_t+D_t-R P_t-1)

j=1

z_j,t-1=

R W_t-1 + (P_t+D_t-R P_t-1) s =

R (W_t-1-s P_t-1) + s D_t + s P_t,

(29)

where s is the total number of shares available to trade. R (W_t-1-s P_t-1) + s D_t is the total amount of money invested in the risk free asset and s P_t is the total amount of money invested in the risky asset by all agents at time t. If the total initial market wealth is equal to W₀, then the total wealth at time t is equal to

W_t=

R^t (W₀-s P₀) + s

t-1

i=0

(Rⁱ D_t-i) + s P_t =

(W₀-s P₀) +

t-1

i=0

(

Rⁱ (r^F (W₀-s P₀)+s D_t-i)

)

+ s P_t .

(30)

Naturally D_tł 0 at each date. Suppose that W₀=M+s P₀, then the total amount of money invested in the risk free asset, W_t-s P_t, at time t is greater than or equal to zero for t=0,...,T, if the initial amount of money invested in the risk free asset, M, is positive. We assume throughout this chapter that M ł 0.

We assume that at time t each of the N agents hands over his demand function (6.27) for the risky asset to a market auctioneer. The auctioneer collects the demand functions and computes the final equilibrium price P_t so that the market clears. Equilibrium of demand and supply so that the market clears yields

j=1

z_j,t =

h=1

ć
ç
ç
č

j Î belief h

z_j,t^h

ö
÷
÷
ř

=s. (31)

By substituting (6.27) in (6.31) the equilibrium equation (6.31) can be rewritten as

h=1

ć
ç
ç
č

j Î belief h

y_t^h W_j,t

P_t

ö
÷
÷
ř

h=1

ć
ç
ç
č

y_t^h

P_t

j Î belief h

W_j,t

ö
÷
÷
ř

h=1

ć
ç
ç
č

y_t^h W_t^h

P_t

ö
÷
÷
ř

=s,

or equivalently

h=1

(

y_t^h W_t^h

)

=s P_t.

(32)

Here W_t^h is the total wealth of all agents who use forecasting rule h at time t. Recall that the demand y_t^h is a function of P_t. To solve the equilibrium equation (6.32) for P_t, we first have to determine how much wealth is assigned to each belief, W_t^h, by all agents. In Appendix B we show that under the assumption that at date t=0 wealth is equally divided among agents and under the assumption that each agent has zero market power at each date, it is true that the fraction of total wealth invested according to belief h at time t converges in probability to the probability that an agent chooses belief h, that is

W_t^h

W_t

q_t^h. (33)

Notice that we use slightly different choice probabilities as in (6.15) by introducing a lower bound on the probabilities as motivated by Westerhoff (2002); see Appendix B for details.

The heterogeneous agents model equilibrium equation

Now that we have shown that the fraction of total market wealth invested according to a certain belief converges in probability to the probability that the belief is chosen, we can solve equation (6.32) for P_t to get the equilibrium price. Equilibrium equation (6.32) can be rewritten as

h=1

ć
ç
ç
č

y_t^h

W_t^h

W_t

P_t

ö
÷
÷
ř

h=1

ć
ç
ç
č

y_t^h q_t^h W_t

P_t

ö
÷
÷
ř

or equivalently

h=1

y_t^h q_t^h =

s P_t

W_t

(34)

The left hand side of equation (6.34) is the demand for the risky asset as a fraction of total wealth, while the right hand side is the worth of the supply of shares as a fraction of the total wealth. Using (6.29) the right hand side can be rewritten to

S(P_t)=

P_t

ć
ç
ç
č

W_t-1

-P_t-1

ö
÷
÷
ř

+D_t+P_t

The first and second derivative of the supply function S(P_t) are equal to

d S(P_t)

d P_t

(c+P_t)²

;

d² S(P_t)

d P_t²

-2 c (c+P_t)

(c+P_t)⁴

where c=R (W_t-1/s-P_t-1)+D_t is the amount of money invested in the risk free asset per risky share. We assume that c>0 (see also equation (6.30)). Thus for P_tł 0 the supply function is a continuous monotonically increasing and concave function of P_t which starts at 0 and converges to 1 as P_t goes to infinity. Notice that this equals the total fraction of wealth invested in the risky asset, which means that the market as a whole never borrows from an outside supplier of money, but that borrowing and lending occurs within the market.

Recall that for the utility maximizing agents the demand as a fraction of individual wealth, y_t^h, in (6.24) is a decreasing function of P_t. For the non utility maximizing agents y_t^h does not depend on P_t, but only on past prices. Hence the left hand side of equilibrium equation (6.34) is a decreasing function of P_t. Although the right hand side of (6.34) is an increasing function of P_t, some additional restrictions for the demand of the non utility maximizing agents must hold for a unique positive equilibrium price to exist. This will be shown in the next section.

The equilibrium price

We split the set of beliefs or forecasting rules the agents can choose from in a set B₁ of utility maximizing beliefs based upon price predictions and the set B₂ of non utility maximizing beliefs, not using price predictions but technical trading strategies. Equation (6.34) can then be rewritten as

h Î B₁

q_t^h y_t^h +

h Î B₂

q_t^h y_t^h =

s P_t

W_t

. (35)

If the supply of outside shares is equal to zero, i.e. s=0, then substituting (6.24) in (6.35) to solve for P_t yields

P_t=

R- a s²

h Î B₂

q_t^h y_t^h

h Î B₁

q_t^h

h Î B₁

q_t^h

h Î B₁

q_t^h

E_t^h(P_t+1+D_t+1).

(36)

Several assumptions have to be made for the equilibrium price to exist. First we have to assume that there is a belief h Î B₁ for which q_t^h>0. If for all beliefs h Î B₁: q_t^h=0, then there is no solution for P_t. Further, for the equilibrium equation to be solvable for P_t an upperbound has to be posed on the fraction of total market wealth the technical traders in B₂ can go long in the risky asset. If s=0, then according to equilibrium equation (6.35) the fraction of total market wealth traders in belief group B₂ go long is equal to the fraction of total market wealth traders in belief group B₁ go short, that is

h Î B₂

q_t^h y_t^h = -

h Î B₁

q_t^h y_t^h.

Because of the characteristics of the demand function (6.24) for the risky asset, traders in belief group B₁ are restricted in the fraction of individual wealth they can go short, that is

a s²

< y_t^h < Ą.

This implies that there is an upperbound on the fraction of total wealth traders in belief group B₂ can go long, that is

h Î B₂

q_t^h y_t^h = -

h Î B₁

q_t^h y_t^h <

a s²

h Î B₁

q_t^h.

This restriction implies that the denominator of the ratio in the first part of the right hand side of (6.36) is positive. There is a positive equilibrium price in the case of zero supply of outside stocks, because price and dividend expectations are restricted to be always positive. If B₂ = Ř, then ĺ_{h Î B₂} (q_t^h y_t^h)=0 and the equilibrium price is equal to the net present value of the average of the expected price plus dividend by the traders in belief group B₁. This is the same solution for the equilibrium price as in the BH model. For s=0 as in the BH model, wealth plays no role anymore. For every short position there must be an offsetting long position. If the gross risk free rate under borrowing and lending is always equal to R, then wealth at time t is just equal to W_t=R W_t-1.

The derivation of the equilibrium price for a strictly positive supply of outside shares, i.e. if s>0, is presented in Appendix C.

The EMH benchmark with rational agents

In a world where all agents are identical, expectations are homogeneous and all traders are risk neutral, i.e. a Ż 0, equilibrium equation (6.36) in the case of s=0 and equilibrium equation (6.61) in the case of s > 0 both reduce to

P_t=

E_t(P_t+1+D_t+1). (37)

This arbitrage market equilibrium equation states that today's price of the risky asset must be equal to the sum of tomorrow's expected price and expected dividend, discounted by the risk-free interest rate. The arbitrage equation (6.37) can be used recursively to derive the price at time t

P_t=

E_t(P_t+k)

R^k

j=1

E_t(D_t+j)

R^j

. (38)

If the transversality condition

lim

k ® Ą

E_t(P_t+k)

R^k

=0,

holds, which means that the long run growth rate of price is less than the discount rate r^f, then the price is equal to the net present value of all future dividends

P_t^*=

lim

k ® Ą

j=1

E_t(D_t+j)

R^j

This price is called the efficient markets hypothesis (EMH) fundamental rational expectations price, or fundamental price for short.

We will focus on the case where for all beliefs h expectations on dividend are equal: E_t^h(D_t+1)=E_t(D_t+1) and where the dividend process is iid with mean D. The fundamental price is then constant and equal to

P^*=

6.3.4 A heterogeneous agents model with fundamentalists
versus moving average traders

Utility maximizing belief: the fundamental trader

Fundamentalists expect that prices return to the fundamental value with speed v, that is

E_t^fund(P_t+1)=P^*+v(P_t-1-P^*), 0Ł v Ł 1.

If v=1, then the fundamental traders make naive price expectations and if v=0, then the fundamental traders expect the price to be always equal to the fundamental value. The fraction of individual wealth invested in the risky asset is then equal to

y_t^fund(P_t)=

P_t

E_t(P_t+1+D_t+1)-R

a s²

P_t

(P^*+v(P_t-1-P^*)+

)-R

a s²

where a>0, s²>0 and R=1+r^f>1.

Non utility maximizing belief: the exponential moving average trader

Moving average traders buy (sell) if the price crosses the moving average from below (above). We use the exponential moving average MA_t=µ P_t + (1-µ) MA_t-1, where the exponential smoothing constant 0<µ<1. The fraction of individual wealth invested in the risky asset is then equal to

y_t^ma = 2 g

x_t+1

1+x_t+1²

, where x_t+1=

P_t-1-MA_t-2

MA_t-2

, g>0 and l>0.

6.3.5 The dynamical system

Using equations (6.36), (6.25) and (6.52) and setting MA_t=MA_t-1 and F_t^h=F_t-1^h the following dynamical system for s=0 is obtained

0.1cm P_t(P_t-1, MA_t-1, F_t^fund, F_t^ma);
MA_t=µ P_t-1 + (1-µ) MA_t-1;
F_t^h=r^F + y_t-2^h (r_t-1^P-r^F) + h F_t-1^h, for h=(fund, ma).

Introducing new variables P_i,t-1=P_t-i and MA_i,t-1=MA_t-i the following eight dimensional dynamical system is derived from the above equations

0.1cm P_1,t=q_t^fund/q_t^fund R - a s² q_t^MA y_t^MA (P^*+v(P_1,t-1-P^*)+D);
P_2,t=P_1,t-1;
P_3,t=P_1,t-2=P_2,t-1;
MA_1,t=µ P_1,t-1 + (1-µ) MA_1,t-1;
MA_2,t=MA_1,t-1;
MA_3,t=MA_1,t-2=MA_2,t-1;
F_t^fund=r^F + y_t-2^fund (P_1,t-1+D_t-1/P_2,t-1-R)- C^fund + h F_t-1^fund;
F_t^ma=r^F + y_t-2^ma (P_1,t-1+D_t-1/P_2,t-1 -R)- C^ma + h F_t-1^ma,

where

0.1cm D_t=D+d_t; d_t ~ N(0, s_d²);
P^*=D/r^F;
q_t^ma=1-q_t^fund , q_t^fund=m^fund+(1-m^fund-m^ma) q_t^fund,
q_t^fund=exp(b F_t^fund)/exp(b F_t^fund)+exp(b F_t^ma);
y_t^ma=2 g x_t-1/1+x_t-1² , x_t-1=1/lP_1,t-1- MA_1,t-1/MA_1,t-1;
y_t-2^fund=1/P_t-2(P^*+v(P_t-3-P^*)+D)-R/a s²=1/P_2,t-1(P^*+v(P_3,t-1-P^*)+D)-R/a s²;
y_t-2^ma=2 g x_t-3/1+x_t-3² , x_t-3=1/lP_t-3- MA_1,t-3/MA_1,t-3=1/lP_3,t-1- MA_3,t-1/MA_3,t-1.

Here m^fund and m^ma are the minimum probabilities with which the fundamental and moving average forecasting rule are chosen; see Appendix B for details. The parameter set is given by

Q={	a>0, s²>0, R>1, b>0, 0Ł vŁ 1, 0<µ<1, g>0,
	l>0, 0Ł h Ł 1, m^fundł 0, m^mał 0, 0 Ł m^fund+m^ma Ł 1,
	C^fundł C^ma ł 0 }.

The difference in probability with which the fundamental and moving average belief are chosen is equal to

q_t^fund-q_t^ma=(m^fund-m^ma) + (1-m^fund-m^ma) tanh

ć
ç
ç
č

(

F_t^fund-F_t^ma

)

ö
÷
÷
ř

As can be seen in the above formula, the higher the difference in fitness in favour of the fundamental belief, the higher the difference in probability in favour of the fundamental belief. The fraction of agents who choose the fundamental believe is restricted to be strictly positive q_t^fund>0, since otherwise there is no solution for the equilibrium price. This condition will be automatically satisfied, even if m^fund=0, because of the discrete choice model probabilities which for finite b are always strictly positive². Furthermore, the following condition should hold for the fraction of total market wealth the moving average traders invest in the risky asset

q_t^ma y_t^ma<q_t^fund

a s²

for otherwise there is also no solution for the equilibrium price.

Note that

lim

s² Ż 0

P_1,t=

lim

a Ż 0

P_1,t =

lim

q_t^ma Ż 0

P_1,t=

lim

y_t^ma Ż 0

P_1,t=

E_t^fund(P_t+1+D_t+1). (39)

Hence, if the conditional variance or the risk aversion of the fundamental belief goes to zero, or if the fraction of wealth invested by the moving average belief goes to zero, then the equilibrium price is equal to the discounted value of the expectation of tomorrow's price and dividend of the fundamental belief.

We define the vector variable

z_t=(P_1,t, P_2,t, P_3,t, MA_1,t, MA_2,t, MA_1,t, F_t^fund, F_t^ma)'.

In the following we denote the dynamical system by F, where

z_t=F(z_t-1).

Additive dynamic noise can be introduced into the system to obtain

z_t=F(z_t-1) + e_t,

where e_t=(e_t, 0,0,0,0,0,0,0)' are iid random variables representing the model approximation error in that our model can only be an approximation of the real world. Because we assumed for all beliefs

V_t^h(r_t+1^P)=V_t^h

ć
ç
ç
č

P_t+1+D_t+1-P_t

P_t

ö
÷
÷
ř

=s²

and because P_t+1 and D_t+1 are independent, this implies

V_t^h(P_t+1)=P_t² s² - V_t^h(D_t+1)=P_t² s² - s_d².

Therefore, when we add dynamic noise to the deterministic skeleton, we draw e_t iid from a normal distribution with expectation 0 and variance

s_{e_t}²=P_t² s² - s_d².

6.4 Trading volume

In this section we describe a procedure to determine trading volume. The total number of short or long positions transferred from belief b to belief h at time t converges in probability to z_t-1^b q_t^h as the number of agents, each having zero market power, converges to infinity. The total number of long and short positions transferred to belief h from the other beliefs converges then in probability to

#long_t(® h)

b=1

z_t-1^b q_t^h I(z_t-1^b ł 0);

#short_t(® h)

b=1

z_t-1^b q_t^h I(z_t-1^b<0) |,

(40)

where I(.) is the indicator function. The demand for shares of each belief, under the equilibrium price which is set by the auctioneer, is equal to

z_t^h=

y_t^h W_t^h

P_t

y_t^h q_t^h W_t

P_t

The turnover of shares in belief h we define to be equal to

if z_t^h>0 then Vol_t^h=|z_t^h-#long_t(® h)| +|#short_t(® h)|;

if z_t^h<0 then Vol_t^h=|z_t^h+#short_t(® h)|+|#long_t(® h)|;

if z_t^h=0 then Vol_t^h=|#long_t(® h)|+|#short_t(® h)|.

(41)

The total turnover of shares is equal to

Vol_t=

h=1

Vol_t^h,

doubly counted. For example, if belief h advises to hold a long position in the market at time t, then first it is determined how many long positions are transferred to belief h from the other beliefs at time t. The change in long positions is given by |z_t^h-#long_t(® h)|. This gives the (minimum) number of stock positions sold or bought to reach the new long position from the old long position. Because a long position in the market is held, the short positions transferred to belief h must be closed, which gives an extra volume of |#short_t(® h)|. Adding the two turnovers together yields the total trading volume in belief h, in the case z_t^h>0. The other cases in (6.41) have a similar explanation.

6.5 Stability analysis

6.5.1 Steady state

For the system to be in the steady state it is required that the memory parameter is restricted to 0 Ł h <1, thus we assume finite memory. A variable x at its steady state will be denoted by x. A steady state for the map F is a point z for which F(z)=z. Hence in the steady state MA=µ P + (1-µ) MA, implying P=MA. Furthermore, P=MA, implies y^MA=0 and hence F^ma=r^F-C^ma/1-h. Thus the steady state price of the risky asset is equal to the steady state exponential moving average of the price. This relation implies that the steady state demand of the moving average belief is equal to zero.

The steady state price must satisfy P=1/R(P^*+v(P-P^*)+D), where P^*=D/r^f is the fundamental price. This implies that P=P^*, y^fund=0 and F^fund=r^F-C^fund/1-h. As for the moving average belief, also the steady state demand of the fundamental belief is equal to zero.

In the steady state the difference in probability with which both beliefs are chosen is equal to

q^fund-q^ma=(m^fund-m^ma) + (1-m^fund-m^ma)tanh

ć
ç
ç
č

-b

2(1-h)

(C^fund-C^ma)

ö
÷
÷
ř

If m^fund=m^ma=0, then because C^fundł C^mał 0, we have that q^fund Ł q^ma. Thus, if no lower bound is imposed on the discrete choice probabilities, then at the steady state the fundamental belief is chosen with smaller probability than the moving average belief if the costs of the fundamental belief are higher than the costs of the moving average belief. Because q^fund+q^ma=1, the steady state probabilities are equal to

q^fund=

ć
ç
ç
č

1+ (m^fund-m^ma) + (1-m^fund-m^ma) tanh

ć
ç
ç
č

-b

2(1-h)

(C^fund-C^ma)

ö
÷
÷
ř

q^ma =1-q^fund.

6.5.2 Local stability of the steady state

The local behavior of the dynamical system z_t=F(z_t-1) around the steady state z is equivalent to the behavior of the linearized system

(z_t-z)=

dF(z_t-1)

d z_t-1

˝
˝
˝
˝

z_t-1=z

(z_t-1-z) = J (z_t-1-z),

if none of the eigenvalues of the Jacobian matrix J lies on the unit circle. Hence we can study the dynamical behavior of the system for different parameter values by calculating the eigenvalues of J. The steady state z is locally stable if all eigenvalues lie within the unit circle and becomes unstable if one of the eigenvalues crosses the unit circle. At this point a bifurcation, a qualitative change in dynamical behavior, occurs.

A straightforward computation shows that the Jacobian matrix of F at the steady state z is equal to

é
ę
ę
ę
ę
ę
ę
ę
ę
ę
ę
ę
ë

2 a g s²

l R

q^ma

q^fund

-2 a g s²

l R

q^ma

q^fund

1-µ

ů
ú
ú
ú
ú
ú
ú
ú
ú
ú
ú
ú
ű

The characteristic polynomial of J evaluated at the steady state is equal to

p(x)= |J-x I|=

x⁴ (h-x)²

ć
ç
ç
č

x²-( 1-µ +

2 a g s²

l R

q^ma

q^fund

)x + (1-µ)

2 a g s²

l R

q^ma

q^fund

ö
÷
÷
ř

(42)

Thus the eigenvalues of J are 0 (with algebraic multiplicity 4), h (with algebraic multiplicity 2) and the roots x₁, x₂ of the quadratic polynomial in the last bracket. Note that these roots satisfy the relations

x₁+x₂=1-µ +

2 a g s²

l R

q^ma

q^fund

and x₁ x₂=(1-µ)

2 a g s²

l R

q^ma

q^fund

, (43)

because

(x-x₁)(x-x₂)=x²-(x₁+x₂)x + x₁ x₂. (44)

Also note that because memory cannot be infinite in the steady state (i.e. 0 Ł h <1), the stability of the steady state is entirely determined by the absolute values of x₁ and x₂. Furthermore, if there is no difference in costs between implementing the fundamental or moving-average strategy, that is C^ma-C^fund=0, then q^ma and q^fund are independent of the intensity of choice parameter b and hence the local stability of the steady state of the heterogeneous agents model is independent of b.

We have seen in (6.39) that if the risk aversion, a, or if the expected dispersion of the return of the fundamental belief, s², goes to zero, then the equilibrium price is entirely determined by the fundamental belief. Now, using (6.42), we find

lim

a Ż 0

p(x) =

lim

s² Ż 0

p(x)=x⁴ (h-x)² (x-

) (x-(1-µ)), (45)

so that the eigenvalues are equal to 0, h, v/R and (1-µ). Because R>v all eigenvalues lie within the unit circle. Hence, in this limiting case, the fundamental steady state is locally stable, because near the fundamental steady state fundamental traders exploit all profit opportunities, driving the price back to the fundamental value.

6.5.3 Bifurcations

A bifurcation is a qualitative change in the dynamical behavior of the system when varying the value of one of the parameters. Bifurcations occur for example, if one of the eigenvalues of the linearized system in the steady state crosses the unit circle. We are now going to investigate local bifurcations of the steady state.

Eigenvalue equal to 1

If one of the eigenvalues crosses the unit circle at 1, a saddle-node bifurcation may arise in which a pair of steady states, one stable and one saddle, is created. Another possibility is that a pitchfork bifurcation arises in which two additional steady states are created. The only possibility for an eigenvalue to be equal to one is that one of the solutions, x_j, of the quadratic polynomial in (6.44) is equal to 1, say x₂=1. Then it follows from (6.43) that

x₁+1=1-µ +

2 a g s²

l R

q^ma

q^fund

and x₁=(1-µ)

2 a g s²

l R

q^ma

q^fund

Eliminating x₁ from these equations leads to the condition

R=v.

However, since 0 Ł v Ł 1 < R, this condition can never be satisfied. Hence eigenvalues equal to 1 can never occur.

Eigenvalue equal to -1

If one of the eigenvalues crosses the unit circle at -1, a period doubling or flip bifurcation may arise in which a 2-cycle is created. Under the assumption that x₂=-1, equations (6.43) lead to the relations

x₁-1=1-µ +

2 a g s²

l R

q^ma

q^fund

and -x_<1=(1-µ)

2 a g s²

l R

q^ma

q^fund

Eliminating x₁ leads to the condition

l (µ-2) (R+v) = 4 a g s²

q^ma

q^fund

Since all parameters in the model are strictly positive and because -2<µ-2<-1, the left hand side of this condition is strictly negative. However the right hand side of the condition is strictly positive, so that this condition can never be satisfied. Hence eigenvalues equal to -1 and therefore period doubling bifurcations of the steady state can never occur.

Two complex conjugate eigenvalues of modulus 1

If a pair of complex conjugate eigenvalues crosses the unit circle in the complex plane, a Hopf or Neimark-Sacker bifurcation may arise in which an invariant circle with periodic or quasi-periodic dynamics is created. The roots x₁, x₂ of the characteristic equation are complex conjugate of modulus 1 if x₁ x₂=1 and |x₁+x₂|<2. Using (6.43) this leads to the conditions

(1-µ)

2 a g s²

l R

q^ma

q^fund

= 1 and |1-µ +

2 a g s²

l R

q^ma

q^fund

|<2. (46)

Substituting the first condition in the second yields

|2-µ

ć
ç
ç
č

ö
÷
÷
ř

|<2.

For 0<µ<1 and 0Ł vŁ 1<R this condition is always satisfied. Hence for parameters satisfying the first condition a Hopf bifurcation should occur. However, when solving the first condition for b, h, v or µ it turns out that not always a Hopf bifurcation occurs when varying one of these four parameters while keeping the other parameters constant, because for these parameters additional restrictions apply.

When solving the first condition for the risk aversion parameter a a Hopf bifurcation occurs given the parameter set {Q} \ a if a_H satisfies

a_H=

ć
ç
ç
č

1-(1-µ)

ö
÷
÷
ř

l R

2 g s²

q^fund

q^ma

>0 .

When solving the first condition for the intensity of choice parameter b a Hopf bifurcation occurs given the parameter set {Q} \ b and C^fund>C^ma if b_H satisfies

b_H=

1-h

C^fund-C^ma

ln(c),

where c is defined as

b (1-m^ma)-m^ma

(1-m^fund)-b m^fund

,with b=

ć
ç
ç
č

1-(1-µ)

ö
÷
÷
ř

l R

2 a g s²

ö
÷
÷
ř

>0.

However, because b ł 0, there are possibly cases for which no Hopf bifurcation occurs, when varying b and keeping the other parameters constant if the logarithm ln(c) is taken over a value smaller than one.

When solving the first condition for the memory parameter h a Hopf bifurcation occurs given the parameter set {Q} \ h if h_H satisfies

h_H=1-

b (C^fund-C^ma)

ln(c)

However, because 0 Ł h < 1, there are cases for which no Hopf bifurcation occurs, when varying h and keeping the other parameters constant.

When solving for the expected dispersion in return parameter s² a Hopf bifurcation occurs given the parameter set {Q} \ s² if s_H² satisfies

s_H²=

ć
ç
ç
č

1-(1-µ)

ö
÷
÷
ř

l R

2 a g

q^fund

q^ma

>0 .

When solving for the gross risk-free interest rate parameter R a Hopf bifurcation occurs given the parameter set {Q} \ R if R_H satisfies

R_H=

2 a g s²

ć
ç
ç
č

1-(1-µ)

ö
÷
÷
ř

q^ma

q^fund

Because R>1, there are possibly cases for which no Hopf bifurcation occurs, when varying R and keeping the other parameters constant.

When solving the first condition for the fundamental belief parameter v a Hopf bifurcation occurs given the parameter set {Q} \ v if v_H satisfies

v_H=

1-µ

ć
ç
ç
č

2 a g s²

l R

q^ma

q^fund

ö
÷
÷
ř

Again however, because 0 Ł v Ł 1, there are cases for which no Hopf bifurcation occurs, when varying v and keeping the other parameters constant.

When solving the first condition for the exponential moving average parameter µ a Hopf bifurcation occurs given the parameter set {Q} \ µ and v>0 if µ_H satisfies

µ_H=1-

2 a g s²

l v

q^ma

q^fund

and where v should additionally satisfy 0<vŁ 1. Now also, because 0 < µ < 1, there are cases for which no Hopf bifurcation occurs, when varying µ and keeping the other parameters constant.

When solving for the moving average belief parameter g a Hopf bifurcation occurs given the parameter set {Q} \ g if g_H satisfies

g_H=

ć
ç
ç
č

1-(1-µ)

ö
÷
÷
ř

l R

2 a s²

q^fund

q^ma

>0 .

When solving for the moving average belief parameter l a Hopf bifurcation occurs given the parameter set {Q} \ l if l_H satisfies

l_H=

2 a g s²

ć
ç
ç
č

1-(1-µ)

ö
÷
÷
ř

q^ma

q^fund

>0.

Hence when one of the parameters a, s², g or l is varied while keeping the other parameters constant, a Hopf bifurcation always arises for some parameter value.

If the Jacobian matrix of F at the steady state z has two complex conjugate eigenvalues, x₁=c+di and x₂=c-di, then the price series, and therefore also the exponential moving average series, follows a wavelike pattern. For fluctuation close to the steady state the period of the wave is approximately equal to

2 p

, where tan(q)=

, with c>0,

if the two complex conjugate eigenvalues are near the unit circle. Solving p(x)=0 under the conditions in (6.46) yields

4-(1-µ+

+K)²

(1-µ+

+K)²

, with K=

2 a g s²

l R

q^ma

q^fund

For 0<µ<1 this is an increasing function of µ and hence q is an increasing function of µ. Thus the period of the wave of the price fluctuation close to the unstable steady state is a decreasing function of µ. Recall that in the computation of the exponential moving average, the larger µ, the more weight is placed on current prices, the more closely the moving average follows the price series, and the more earlier a change in direction of the price series is detected. Thus, a larger µ causes price to return to the fundamental value with a higher frequency than a smaller µ.

6.6 Numerical analysis

In the last section we studied the local stability of the steady state analytically. We determined what kind of bifurcations can occur if the value of one of the model parameters is varied. In this section we study the global dynamical behavior numerically, especially when the steady state is unstable, with the aid of time series plots, phase diagrams, delay plots, bifurcation diagrams and the computation of Lyapunov exponents.

6.6.1 Lyapunov characteristic exponents

The Lyapunov characteristic exponents (LCEs) measure the average rate of divergence (or convergence) of nearby initial states, along an attractor in several directions. Consider the dynamical model z_t+1=F(z_t), where F is a k-dimensional map. After n periods the distance between two nearby initial state vectors z₀ and z₀+v₀ has grown approximately to

||Fⁿ(z₀+v₀)-Fⁿ(z₀)|| » ||DFⁿ(z₀) v₀ ||,

where v₀ is the initial perturbation vector, DFⁿ(z₀) is the Jacobian matrix of the n-th iterate of F evaluated at z₀ and ||.|| denotes the Euclidean distance. The exponent l(z₀, v₀) measuring the exponential rate of divergence has to satisfy

||Fⁿ(z₀+v₀)-Fⁿ(z₀)|| » ||DFⁿ(z₀) v₀ || = e^{n l(z₀, v₀)} ||v₀||.

For a k dimensional system there exist k distinct LCEs, ordered as l₁ ł l₂ ł ... ł l_k, each measuring the average expansion or contraction along an orbit in the different directions. The largest LCE can be defined as

l(z₀, v₀)=

lim

n ® Ą

ln(||DFⁿ(z₀) v₀ ||). (47)

To calculate the largest LCE we thus have to determine ||DFⁿ(z₀) v₀ ||. We set the initial perturbation vector v₀ with ||v₀||=e, where e is some small number. We define

F(z_i + v_i)-F(z_i) » DF(z_i) v_i = v_i+1' = f_i+1 v_i+1, (48)

where v_i is a perturbation vector on the i-th iterate of F (i.e. z_i=Fⁱ(z₀)) and f_i+1 is a scalar. We define

v_i+1=

v_i+1'

||v_i+1'||

e, so that ||v_i+1||=||v_i||=...=||v₀||=e. (49)

Using the chain rule for DFⁿ(z₀) we get

DFⁿ(z₀) v₀ = DF(z_n-1)...DF(z₁) DF(z₀) v₀.

Using (6.48) recursively this relation transforms to

DFⁿ(z₀) v₀ = f_n...f₂ f₁ v_n.

Because

lim

n ® Ą

ln(||v_n||)=0,

the LCE in equation (6.47) can be written as

l(z₀, v₀)=

lim

n ® Ą

i=1

ln(f_i). (50)

Hence we can confine ourselves to the calculation of

f_i=

||v_i'||

||v_i||

||v_i'||

, for i=1...n (51)

to determine the largest LCE.

Numerically we compute the largest LCE as follows. Given an initial perturbation vector v₀, the approximation in (6.48) is used to determine v_i+1' for i ł 0, that is
F(z_i + v_i)-F(z_i) » v_i+1'. Next we compute the perturbation vector for the i+1-th iterate by using (6.49). The factor f_i+1 is computed by using (6.51). Finally, for large n, the largest LCE is computed by using (6.50).

Attractors may be characterized by their Lyapunov spectrum. For a stable steady state or a stable cycle all LCEs are negative. For a quasi-periodic attractor the largest LCE is equal to zero, while all other LCEs are negative. An attractor is called a strange or a chaotic attractor if the corresponding largest LCE is positive, implying sensitive dependence on initial conditions.

6.6.2 Parameter values

In our numerical analysis of the heterogeneous agents model with evolutionary learning we want to choose values for the model parameters which are economically sensible. We assume that there are 250 trading days in one year. The trading interval in our model is 1 day. If we are talking about daily frequencies, then the order of magnitude of percentage price changes is in basis points (1/100 of 1%).

We set the risk-free interest rate to 5% at a yearly basis with daily compounding. Thus r^f=0.05/250=0.0002, that is 2 basis points daily. The daily standard deviation of the Dow-Jones Industrial Average during the twentieth century is equal to 1.0830%, which translates to a yearly standard deviation of, if we assume that returns are independently distributed, 1.0830*250 » 17%. We take this number as the standard deviation of the returns, that is s=0.010830. Dividends are assumed to be iid and the mean dividend is set to 50 yearly, paid daily. Hence the fundamental value of the risky asset under the iid assumption is equal to 50/0.05=1000. The standard deviation of the dividend process is set equal to 10 yearly.

We choose the exponential moving average parameter µ to be equal to 0.18. The maximum fraction of individual wealth a moving average trader can go long or can go short in the risky asset we choose to be equal to g=1.25 and occurs when the price deviates from the moving average with 7 basis points (l=0.0007).

The fundamental value expectations parameter v we choose to be equal to 0.99. Because

E_t^fund(P_t+1)=P^* + v (P_t-1-P^*) ,

the expected two-day return of the stock price, not corrected for dividends, is equal to

E_t^fund(P_t+1)-P_t-1

P_t-1

=(1-v)

P^*-P_t-1

P_t-1

Thus, if the price should decline by 2% to return to the fundamental value P^*, then for v=0.99 the fundamental trader expects that the two-day price return is equal to 2 basis points, which corresponds with a one-day price return of 1 basis point.

A broad range of studies, taking into account the full range of available assets, places the degree of risk aversion a for the representative investor in the range of 2 to 4, see for example Friend and Blume (1975), Grossman and Shiller (1981). We set a initially to 4.

Costs for implementing the strategy with fundamental beliefs are higher than the costs for implementing the exponential moving-average strategy. We set the costs of determining the fundamentals to 1 basis point daily (C^fund=0.0001), which is 2.5% yearly. The costs of the moving-average strategy we set to zero.

The discrete choice model determines on the basis of the fitnesses of the beliefs with which probabilities the moving average and fundamental beliefs are chosen by the agents. The memory parameter, h, we choose to be equal to 0.25. We choose the intensity of choice parameter, b, to be equal to 250. The minimum probabilities with which the fundamental belief, m^fund, and the moving average belief, m^ma are chosen, we set equal to 0.01.

6.6.3 Model simulations

Bifurcations

We have seen in equation (6.45) that in the case of risk neutrality of the fundamental traders, i.e. a=0, there is locally always convergence to the fundamental steady state. If a=4, then for b=0 the dynamical system exhibits quasi periodic behavior and no change in the dynamics occurs by increasing b. Only for a<0.456 changes in the dynamical behavior can be observed by varying b. Therefore we set the risk aversion parameter a initially low (0.42), so that the local dynamics around the steady state is dependent on the intensity of choice parameter b.

For a=0.42 figure 6.3a shows the bifurcation diagram with respect to b. A Hopf bifurcation occurs at b_H=635. Figure 6.3b shows the corresponding largest LCE plot. Before the Hopf bifurcation occurs the largest LCE is clearly smaller than zero, indicating convergence to the steady state. After the Hopf bifurcation occurred, the largest LCE is close to zero, indicating quasi periodic dynamical behavior. Thus for costs and low risk aversion for the fundamental traders and low intensity of choice for all traders, the price locally converges to the fundamental value. However for high intensity of choice, traders quickly change to the most profitable strategy and the moving-average trading strategy can survive in the market even for low risk aversion of the fundamental traders. Price fluctuations are then driven by the evolutionary dynamics between the two different beliefs.

If the costs for the fundamental traders decrease to zero, then locally when varying b there is always convergence to the fundamental steady state, for low risk aversion. Fundamental expectations then dominate the moving-average strategy. Hence, costs can cause the fundamental steady state to become unstable, even if the risk aversion of fundamental traders is low. In the case of no costs and b=250, figure 6.4a shows the bifurcation diagram with respect to the parameter a, when a is varied between 0.1 and 5. Figure 6.4b shows the corresponding largest LCE plot. At a_H=0.456 a Hopf bifurcation occurs and the dynamics shows quasi periodic behavior after the Hopf bifurcation. Hence, if fundamental traders become more risk averse, then even in the no cost case, moving average traders can survive in the market and affect the price by their actions.

We set a equal to 4 and study the local dynamical behavior when varying the exponential moving average parameter µ. To observe a change in the dynamical behavior for the parameter µ we double the parameter l to 14 basis points and we decrease the intensity of choice parameter b to 125. Figure 6.5a shows the bifurcation diagram with respect to µ, if µ is varied between 0.04 and 0.98. Figure 6.5b shows the corresponding largest LCE plot. Remember that by increasing the parameter µ the moving average follows the price series more closely and generates earlier a trading signal when the directional trend in prices changes direction. From the bifurcation diagram and the LCE plot it can be seen that the fundamental steady state becomes locally stable if the technical traders use a very fast moving average (µ>0.82), that is if the technical traders quickly change their trading position if the directional trend in prices changes direction. For lower values of µ the LCE plot is close to zero and thus the dynamical system exhibits quasi periodic behavior.

Price simulations

Figures 6.6a, b, c and d show, given the parameter values in section 6.6.2, the time series plots of the price, return, fraction of fundamental traders and trading volume. The price series plot shows that there is a slow movement away from the fundamental value and a quick movement back. In figure 6.6a price starts below the fundamental value of 1000 and slowly increases with a declining positive return, or stated differently, the price sequence is concave. As price is increasing further and further above the fundamental value of 1000, the fundamental traders go short a larger fraction of their wealth, causing volume to increase as can be seen in figure 6.6d. The fraction of fundamental traders starts below 0.50 and is slowly increasing until the point that stock returns become smaller than the risk-free interest rate. Then the moving average forecasting rule is not profitable anymore and the fraction of fundamental traders increases sharply until approximately 0.56. These fundamental traders cause the price to turn back in the direction of the fundamental value. This change in trend is picked up by the moving average traders and they reinforce the downtrend by holding also short positions in the risky asset. Because as well the fundamental traders as the moving average traders are expecting price to decline, price falls quickly back to the fundamental value in a convex way. However, because the moving average traders are doing better than the fundamental traders, the fraction of fundamental traders declines sharply. Thus, the fundamentalists change the direction of the trend, but the chartists push prices back to the fundamental value. Because a majority of the agents was following the fundamental forecasting rule and already had short positions before the turn in price direction, volume drops sharply after the change of direction in the price trend. As price returns to the fundamental value, agents following the fundamental belief are closing their short positions, while traders following the moving average belief are holding more and more short positions, causing volume to increase. After prices dropped back to the fundamental value, prices keep on declining due to the moving average traders, with negative but increasing returns, so that the price sequence is convex. Volume increases, because traders following the fundamental belief are now holding more and more long positions as price moves below the fundamental value. Then, if the short position held by the moving average traders is not profitable anymore, the fraction of fundamental traders increases sharply turning the downward trend in price to an upward trend in price. The moving average traders detect the change in trend and will change their short position to a long position in the risky asset, causing price to increase back to the fundamental value. Because a majority of the agents was following the fundamental forecasting rule and already had long positions, volume drops sharply after the change of direction in the price trend. The price cycle is thus characterized by a period of small price changes when moving average traders dominate the market and periods of rapid decrease or increase of prices when fundamental traders temporarily dominate the market. Furthermore, volume goes by the prevailing trend as can be seen in figure 6.6d. That is, if the primary trend is upwards, then volume increases. Volume drops during a change in directional trend. Then, if the primary trend is downwards, volume also increases. This is a very important concept in technical analysis and the relation has been shown in many price charts.

Adding dynamic noise to the deterministic skeleton leads to irregular price behavior as can be seen in figure 6.7a. Clearly periods with trending behavior can be identified. Figure 6.7c shows that the fraction of fundamental traders is switching irregular between its lower- and upperbound. Because little autocorrelation, volatility clustering and fat tails are important characteristics of real financial time series, we check our return series for these features. Figures 6.8b and 6.8c show the autocorrelation function plots of the returns and the squared returns up to order 36. Figure 6.8b shows that the return series does not exhibit any serial autocorrelation, which means that price changes are linearly independent. Further, according to figure 6.8c the squared return series does not exhibit any serial autocorrelation, which means that there is no volatility clustering present in the data. The return distribution does show excess kurtosis relatively to the normal distribution (see figure 6.8a). Thus our theoretical heterogeneous agents model only fails in mimicking the feature of volatility clustering.

6.7 Conclusion

In this chapter we have built a financial market model with heterogeneous adaptively learning agents, fundamentalists and technical traders. The model is an extension of the Brock and Hommes (1998) model in that it extends the set of trading techniques the agents can independently choose from with a realistic moving-average technical trading rule. Moving averages are well known and one of the mostly used technical indicators in financial practice and therefore they deserve to be implemented in heterogeneous agents modeling. Furthermore, the model is derived under the assumption of relative risk aversion, instead of absolute risk aversion as in the Brock and Hommes (1998) case.

The model is derived under the assumption of infinitely many agents, who only differ in the forecasting rule they select each period. Under the assumption that each agent has zero market power at each date, that is his individual investment decision will not influence the equilibrium price, it is shown that the fraction of total market wealth invested by all agents according to a certain belief converges in probability to the probability that the belief is chosen by the agents. Under the assumption of zero supply of outside stocks and the use of certain beliefs types it turns out that the price equilibrium formula is exactly the same as in Brock and Hommes (1998), namely that the price is equal to the discounted value of the average expected price and dividends by all agents. Moreover if the moving-average technical trading rule is added to the model, then also risk aversion and expected dispersion of future returns play a role in our model.

In the end, our financial market model is an eight dimensional nonlinear dynamical system. The steady state price is equal to the fundamental value, which is the discounted value of all future dividends. Analytically we derive the eigenvalues of the linearized system and we examine for which parameter values bifurcations occur. It is shown that the system only can exhibit a Hopf bifurcation. We use numerical tools such as delay, phase and bifurcation diagrams, and computation of Lyapunov characteristic exponents to study the local stability around the fundamental steady state. If there is no difference in costs of applying the fundamental or moving-average strategy, then it is found that the intensity of choice parameter, measuring how quickly traders switch beliefs, has no influence on the dynamical behavior. In the presence of costs, if the risk aversion parameter of the fundamental traders is low enough, then these traders always drive prices back to the fundamental steady state for the case the intensity of choice parameter is sufficiently low. For high values of the intensity of choice parameter, even for low risk aversion, quasi periodic price behavior can occur as a consequence of a Hopf bifurcation. If costs of all trader types are set to zero and if more realistic values for the risk aversion parameter are chosen, then fundamental traders are too risk averse to drive prices to the fundamental steady state and the price exhibits quasi periodic behavior. However, if the risk aversion parameter is high and the technical traders use a very fast moving average, which follows the price closely, then the price does converge to the fundamental value.

We study a case in which we choose parameter values that are economically sensible. The solution of the dynamical system is quasi periodic price behavior. Interaction between fundamentalists and technical analysts may thus destabilize the market and lead to persistent price fluctuations around an unstable fundamental steady state. It turns out that fundamental traders change the direction of a prevailing price trend, but that once the direction has changed, the technical traders push prices back to the fundamental value. Moreover it is found that volume goes by the prevailing trend, that is if the primary trend is upwards or downwards, then volume increases, only dropping if a change in the direction of the trend occurs. This is an important concept in technical analysis. Dynamic noise to the deterministic skeleton is added and leads to irregular price behavior. The features of the return distribution of the dynamical system are examined, but it is concluded that although the model generates returns series which show zero autocorrelation and fat tails, the model fails in mimicking the important characteristic of volatility clustering.

Appendix

A. Figures

(a)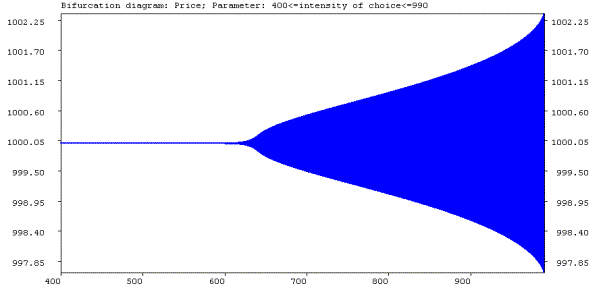

(b)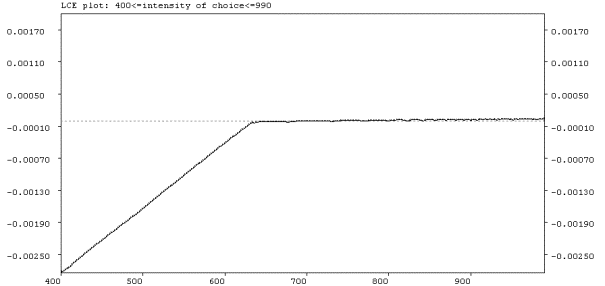

Figure 6.3: (a) Bifurcation diagram for the intensity of choice parameter b with a Hopf bifurcation leading to quasi-periodic dynamics; (b) largest LCE plot.

(a)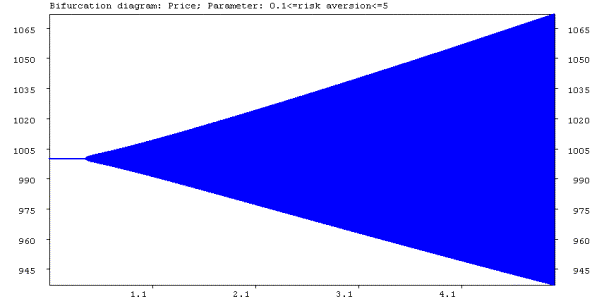

(b)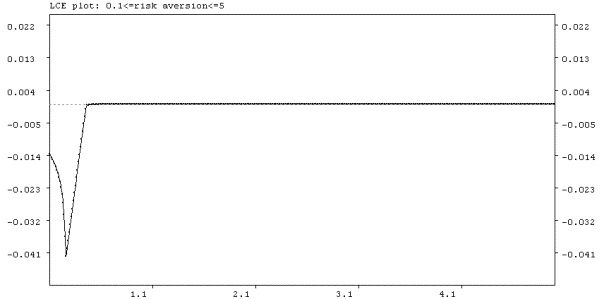

Figure 6.4: (a) Bifurcation diagram for the risk aversion parameter a with a Hopf bifurcation leading to quasi-periodic dynamics; (b) largest LCE plot.

(a)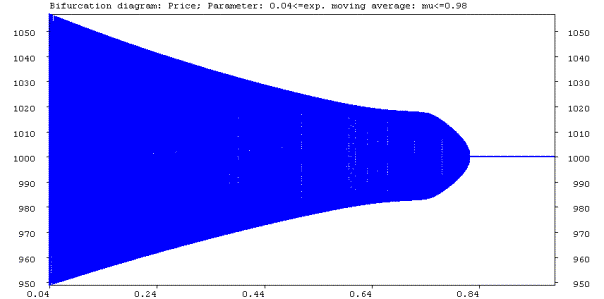

(b)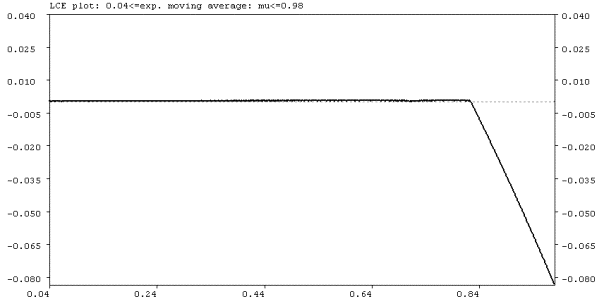

Figure 6.5: (a) Bifurcation diagram for the exponential moving average parameter µ with a Hopf bifurcation leading to quasi-periodic dynamics; (b) largest LCE plot.

(a)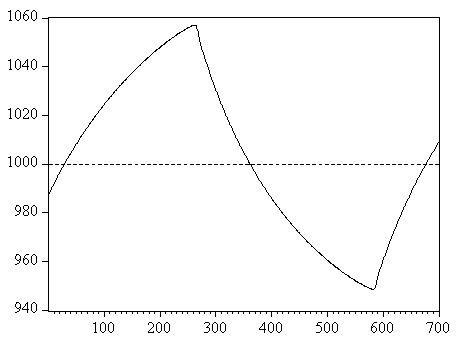

(b)

(c)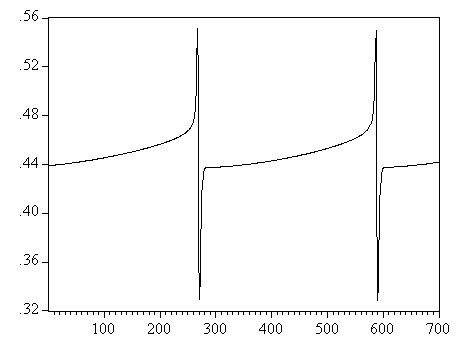

(d)

Figure 6.6: r_f=0.05/250, D=50/250, a=4, µ=0.18, g=1.25, l=0.0007, v=0.99, h=0.25, b=250, m^fund=m^ma=0.01, C^fund=0.0001, C^ma=0. (a) Price plot. Dotted line is the fundamental value; (b) Return plot. Dotted line is the risk-free interest rate; (c) Fraction of fundamental traders; (d) Trading volume.

(a)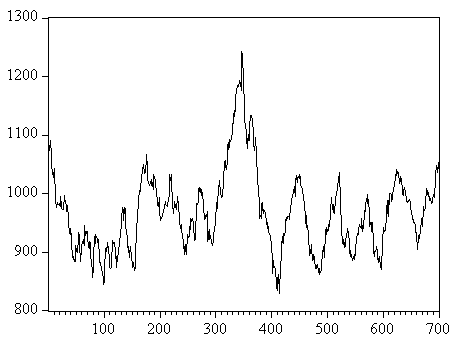

(b)

(c)

(d)

Figure 6.7: Adding dynamic noise to the deterministic skeleton of the nonlinear financial market model with fundamentalists versus moving average traders: s²=0.17/250, s_d²=10/250. (a) Price plot; (b) Return plot. Dotted line is the risk-free interest rate; (c) Fraction of fundamental traders; (d) Trading volume.

(a)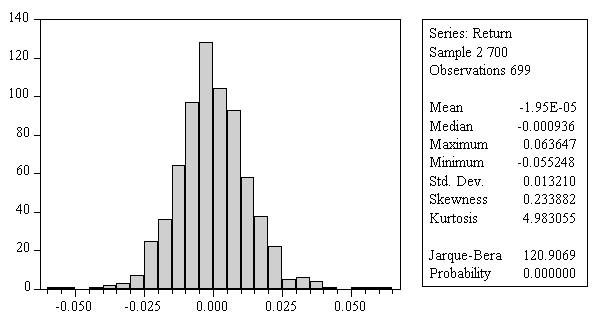

(b)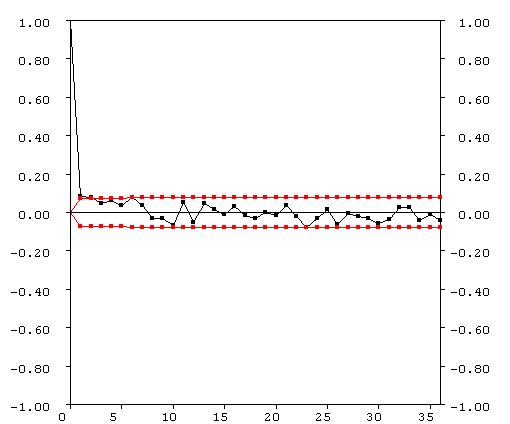

(c)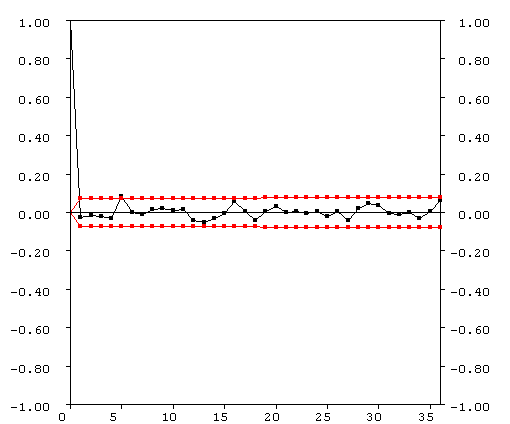

Figure 6.8: (a) Histogram and summary statistics; (b) Autocorrelation function of the returns; (c) Autocorrelation function of the squared returns.

B. Wealth invested according to belief h

Choice probability

The probability that agent j chooses belief h is determined by the discrete choice model in (6.15). The return of belief h in period t is equal to: r^F+y_t-1^h(r_t^P-r^F). Therefore the fitness measure is defined as

F_j,t^h=r^F+y_t-1^h(r_t^P-r^F) - C_j^h +h_j F_j,t-1^h; (52)

As in the BH model it is assumed that for all agents b_j=b, h_j=h and C_j^h=C^h. However, we adjust the probabilities with which each belief is chosen by introducing a lower bound m^h on the probabilities as motivated by Westerhoff (2002):

q_t^h=

exp(b F_t-1^h)

k=1

exp(b F_t-1^k)

;

q_t^h=m^h+(1-

h=1

m^h) q_t^h,

where m^hł 0 " h and 0 Ł ĺ_h=1^H m^h Ł 1. For example, Taylor and Allen (1990, 1992) found in questionnaire surveys that a small group of traders always uses technical or fundamental analysis and do not switch beliefs³. We define X_j,t^h=1 if agent j chooses belief h at time t and X_j,t^h=0 if agent j chooses a belief other than belief h. Because X_1,t^h, ..., X_N,t^h are iid with E(X_j,t^h)=q_t^h and limited variance V(X_j,t^h)=q_t^h (1-q_t^h), the fraction of agents who choose belief h converges in probability to q_t^h:

j=1

X_j,t^h

q_t^h,

as the number of agents goes to infinity. Furthermore we did assume that all agents have the same risk aversion parameter a_j=a, so that agents who follow the same belief have the same demand. Hence in the end we assume that agents are only heterogeneous in the beliefs they can choose from.

Wealth assigned to belief h by agent j

The wealth invested according to belief h by agent j at time t is equal to W_j,t^h=X_j,t^h W_j,t. From this it follows that the total wealth assigned to belief h by all agents is equal to W_t^h=ĺ_j=1^N W_j,t^h. Finally, total market wealth is equal to W_t=ĺ_h=1^H W_t^h. The expected wealth transferred from agent j to belief h conditioned on the wealth of agent j and the information set I_t={P_t-i, D_t-i; ił 0} is equal to:

E(W_j,t^h|I_t, W_j,t)=W_j,t E(X_j,t^h|I_t)= W_j,t (q_t^h 1 + (1-q_t^h) 0)=q_t^h W_j,t.

The expectation of wealth transferred from agent j to belief h conditioned only on I_t is equal to:

E(W_j,t^h|I_t)=E(E(W_j,t^h|I_t, W_j,t)|I_t)=q_t^h E(W_j,t|I_t).

According to (6.28) the wealth of agent j at time t depends on the fraction of the wealth invested at time t-1 and this chosen fraction depends on the agent's belief at time t-1. Hence the expected wealth of agent j at time t conditioned on his wealth at time t-1 is equal to:

E(W_j,t|I_t, W_j,t-1)=

h=1

ć
ç
ç
č

R W_{j, t-1} + (P_t+D_t-R P_t-1)

y_t-1^h W_{j, t-1}

P_t-1

ö
÷
÷
ř

q_t-1^h

ö
÷
÷
ř

R W_{j, t-1} + (P_t+D_t-R P_t-1)

E(y_t-1) W_{j, t-1}

P_t-1

where E(y_t-1)=ĺ_h=1^H y_t-1^h q_t-1^h. The expected wealth of agent j at time t only conditioned on I_t is equal to:

E(W_j,t|I_t)=E_{W_j,t-1}(E(W_j,t|I_t, W_j,t-1)|I_t)=

{W_j,t-1}

E(W_j,t|I_t, W_j,t-1) P(W_j,t-1)=

R E(W_{j, t-1}|I_t-1) + (P_t+D_t-R P_t-1)

E(y_t-1) E(W_{j, t-1}|I_t-1)

P_t-1

. (53)

In the end:

E(W_j,t|I_t)=

ć
ç
ç
č

R +

(P_t+D_t-R P_t-1)

P_t-1

E(y_t-1)

ö
÷
÷
ř

E(W_{j, t-1}|I_t-1)=

(1+r^F + (r_t^P-r^F) E(y_t-1) ) E(W_{j, t-1}|I_t-1),

which is a recursive formula for the expected wealth of agent j at time t given the dividends paid and given the equilibrium prices {P_t-i: i ł 0 } the auctioneer did set. Given the wealth of agent j at time 0, the expected wealth of agent j at time t is equal to:

E(W_j,t|I_t)= W_j,0

t-1

i=0

(

1+r^F + (r_t-i^P-r^F) E(y_t-1-i)

)

Assume that at time 0, all agents have equal initial wealth. Thus for all j we have W_j,0=w₀ and

E(W_j,t|I_t)=w₀

t-1

i=0

(

1+r^F + (r_t-i^P-r^F) E(y_t-1-i)

)

. (54)

According to (6.54) the expectation is equal for all agents at time t, E(W_j,t|I_t)=w_t, under the assumption that all agents have the same wealth at time 0. Finally we now have found that E(W_j,t^h|I_t)=q_t^h w_t " j.
The variance of W_j,t^h conditioned on I_t is equal to:

V(W_j,t^h\|I_t)	=	E((W_j,t^h)²\|I_t)-E²(W_j,t^h\|I_t)
	=	q_t^h E(W_j,t²\|I_t)- (q_t^h)² E²(W_j,t\|I_t)
	=	q_t^h V(W_j,t\|I_t) + q_t^h (1-q_t^h) E²(W_j,t\|I_t).

(55)

The expectation of the squared value of the wealth of agent j at time t conditioned on I_t and his wealth at t-1 is equal to:

E(W_j,t²|I_t, W_j,t-1)=R² W_j,t-1²+2R W_j,t-1² (r_t^P-r^F) E(y_t-1) + W_j,t-1² (r_t^P-r^F)² E(y_t-1²),

and the expectation only conditioned on I_t is equal to:

E(W_j,t²|I_t)=[R² +2R (r_t^P-r^F) E(y_t-1) + (r_t^P-r^F)² E(y_t-1²)] E(W_j,t-1²|I_t-1),

which iterates to:

E(W_j,t²|I_t)=W_j,0²

t-1

i=0

[R² +2R (r_t-i^P-r^F) E(y_t-1-i) + (r_t-i^P-r^F)² E(y_t-1-i²)], (56)

where W_j,0 is the initial wealth of investor j. The square of the expectation of the wealth of agent j at time t is equal to:

E²(W_j,t|I_t)=[R² +2R (r_t^P-r^F) E(y_t-1) + (r_t^P-r^F)² E²(y_t-1)] E²(W_j,t-1|I_t-1),

which iterates to:

E²(W_j,t|I_t)= W_j,0²

t-1

i=0

[R² +2R (r_t-i^P-r^F) E(y_t-1-i) + (r_t-i^P-r^F)² E²(y_t-1-i)]. (57)

Substituting (6.56) and (6.57) in (6.55) gives the variance of the wealth of agent j assigned to belief h at time t conditioned on I_t. If W_j,0=w₀ for all agents, then the variance is equal for all agents, V(W_j,t^h|I_t)=s_h,t² for all j. As a simple example we can take the return of the risky asset to be equal to the risk free rate for t=1,...,T. Then

E(W_j,T^h|I_T)=q_T^h R^T w₀,

V(W_j,T^h|I_T)=q_T^h (1-q_T^h) (R^T w₀)².

Hence in this simple example expected wealth and variance of wealth transferred by agent j to belief h both increase in time.

Fraction of total market wealth assigned to belief h by all agents

We define

W_j,t^h=

W_j,t^h

W_t

as the individual wealth assigned by agent j to belief h as a fraction of total market wealth W_t. The choices agents make at time t are dependent on the performances of the different beliefs until and including time t-1, hence the choices are independent of the price and wealth at time t. However, the price set at time t, which influences the wealth of each agent at time t and thus total wealth, is dependent on the choice of each agent at time t. Thus W_1,t^h, ... , W_N,t^h given I_t are dependent. However, if an agent is very small relative to the market, his choice will have a negligible effect on the eventual price set at time t. Hence if we assume that the market power of each agent is zero, that is

" t Ů " j:

lim

N ® Ą

W_j,t

W_t

® 0, (58)

then the law of large numbers still holds. Thus W_1,t^h, ... , W_N,t^h given I_t are dependent but identically distributed with mean E(W_j,t^h|I_t)=q_t^h w_t/W_t and finite (under assumption 6.58) variance V(W_j,t^h|I_t), so that

j=1

( W_j,t^h)=

W_t^h

W_t

q_t^h

w_t

W_t

. (59)

This means that the average wealth per agent which is assigned to belief h as a fraction of total market wealth converges in probability to q_t^h w_t/W_t as the number of agents goes to infinity. Average wealth per agent as a fraction of total wealth converges to:

W_t

h=1

W_t^h

W_t

h=1

q_t^h

w_t

W_t

w_t

W_t

. (60)

If we divide (6.59) by (6.60) we find that the fraction of total wealth invested according to belief h at time t converges to:

W_t^h

W_t

q_t^h.

C. Equilibrium price for s>0

If s>0, then the derivation of the equilibrium price becomes more complex. By substituting (6.24) and (6.29) in (6.35) we can rewrite (6.35) as the solution to a quadratic equation of P_t. The formulas for the equilibrium price P_t are:

c₁=

h Î B₁

q_t^h

c₃

E_t^h(P_t+1+D_t+1);

c₂=R(W_t-1-s P_t-1)+s D_t;

c₃=

h Î B₁

q_t^h;

c₄=

h Î B₂

q_t^h y_t^h;

Discr=(c₁ c₃ R s + c₂ c₃ R - a c₂ c₄ s²)² + 4 a c₁ c₂ c₃ R s s²;

P_t=

(c₁ c₃ R s-c₂ c₃R + a c₂ c₄ s²) + Discr

2 s (c₃ R + a (1-c₄) s²)

(61)

Here c₁ is the net present value of the average of the expected future price plus dividend by all agents in belief group B₁, c₂ is the total amount of money invested in the risk free asset by all agents, c₃ is the total fraction of market wealth assigned to beliefs in group B₁ and c₄ is the fraction of market wealth invested in the risky asset by agents in belief group B₂ at time t. For the equilibrium equation to be solvable for P_t it is necessary that there is a belief h Î B₁ for which q_t^h>0. If for all beliefs h Î B₁: q_t^h=0, then there is no solution for P_t. Further, an upperbound should be imposed on the fraction of total market wealth traders in group B₂ can go long in the market. If s>0, then the fraction of total market wealth invested in the risky asset lies between 0 and 1, that is

0 Ł

h Î B₁

q_t^h y_t^h +

h Î B₂

q_t^h y_t^h < 1,

or equivalently

h Î B₁

q_t^h y_t^h Ł

h Î B₂

q_t^h y_t^h < 1-

h Î B₁

q_t^h y_t^h.

Because of the characteristics of the demand function (6.24) for the risky asset, traders in belief group B₁ are restricted in the fraction of individual wealth they can go short, that is

a s²

<y_t^h<Ą

This implies that there is an upperbound on the fraction of total wealth traders in belief group B₂ can go long, that is

h Î B₂

q_t^h y_t^h <1+

a s²

h Î B₁

q_t^h , or equivalently c₄<1+c₃

a s²

Thus the denominator in (6.61) is positive. Now the question is whether the nominator of (6.61) is also positive, so that there is a unique positive equilibrium price. It is clear that c₁ł 0. If the initial wealth invested in the risk free asset is positive, then according to (6.30) the total wealth at time t should be at least be equal to the value of the total number of shares: W_t=c₂+ s P_t ł s P_t, implying c₂ ł 0. Because for all beliefs h: q_t^h ł 0 it is also true that c₃ł 0. c₄ Î IR and can be of either sign. Hence under these relationships the nominator of (6.61) is positive, because:

(c₁ c₃ R s-c₂ c₃R + a c₂ c₄ s²) + Discr >

(c₁ c₃ R s-c₂ c₃R + a c₂ c₄ s²) + (c₁ c₃ R s + c₂ c₃ R -a c₂ c₄ s²)²= 2 c₁ c₃ R s > 0.

We have shown that the nominator and denominator of (6.61) are both positive, so that we have proven that for s>0 the model yields a unique positive equilibrium price.

1: Henceforth abbreviated as BH.
2: However, if F_t^ma-F_t^fund becomes large which causes q_t^fundŻ0, this can cause numerical problems in computing the market equilibrium price, because of floating point errors in the computer simulations. These problems are avoided by placing a lower bound m^fund>0 on the probability with which the fundamental belief is chosen.
3: Moreover, especially in our final two type trader model, by placing a lower bound on the probabilities, we can avoid numerical problems in computing the market equilibrium price, because of floating point errors in the computer simulations.

Gerwin Griffioen's Technical Analysis Pages

Chapter 6 An Evolutionary Adaptive Learning Model with Fundamentalists and Moving Average Traders

6.1 Introduction

6.2 The Brock-Hommes heterogeneous agents model

Demand

Market equilibrium

Evolutionary dynamics

6.3 A modified heterogeneous agents asset pricing model

6.3.1 Utility-maximizing beliefs

6.3.2 Non-utility-maximizing beliefs: technical traders

6.3.3 Market equilibrium

Wealth per agent, total wealth and market clearing

The heterogeneous agents model equilibrium equation

The equilibrium price

The EMH benchmark with rational agents

6.3.4 A heterogeneous agents model with fundamentalists versus moving average traders

Utility maximizing belief: the fundamental trader

Non utility maximizing belief: the exponential moving average trader

6.3.5 The dynamical system

6.4 Trading volume

6.5 Stability analysis

6.5.1 Steady state

6.5.2 Local stability of the steady state

6.5.3 Bifurcations

Eigenvalue equal to 1

Eigenvalue equal to -1

Two complex conjugate eigenvalues of modulus 1

6.6 Numerical analysis

6.6.1 Lyapunov characteristic exponents

6.6.2 Parameter values

6.6.3 Model simulations

Bifurcations

Price simulations

6.7 Conclusion

Appendix

A. Figures

B. Wealth invested according to belief h

Choice probability

Wealth assigned to belief h by agent j

Fraction of total market wealth assigned to belief h by all agents

C. Equilibrium price for s>0

Chapter 6
An Evolutionary Adaptive Learning Model with Fundamentalists and Moving Average Traders

6.3 A modified heterogeneous agents
asset pricing model

6.3.4 A heterogeneous agents model with fundamentalists
versus moving average traders