Segunda ley de Newton
La Dinámica es la rama de la mecánica que estudia los cuerpos en movimiento y las fuerzas que intervienen.
Las leyes de Newton para el movimiento de los cuerpos han sido formuladas de una gran variedad de formas. Para nuestro propósito, las expresamos como sigue:
Una partícula bajo el efecto de un sistema de fuerzas equilibradas tiene aceleración nula.
Una partícula bajo el efecto de un sistema de fuerzas no equilibradas tiene una aceleración directamente proporcional a la resultante del sistema de fuerzas y paralela a ella.
Las fuerzas de acción y de reacción entre dos partículas son siempre iguales y de direcciones contrarias.
Peso de un cuerpo. El peso de un cuerpo es la fuerza de atracción gravitacional ejercida sobre el cuerpo por la Tierra y depende de su posición respecto al centro de la Tierra.
Masa de un cuerpo. La masa M de un cuerpo es la cantidad de materia que contiene y es independiente del lugar donde se encuentre; también se le conoce como masa inercial ya que representa la inercia de un cuerpo, es decir la resistencia de un cuerpo al cambio en su movimiento.
A la razón entre el
peso P de un cuerpo y la constante gravitacional g:
,
se le conoce como masa gravitacional M. Pero como el peso y la constante
gravitacional varían de acuerdo a su posición con respecto al centro de la
Tierra, no se ha podido demostrar ninguna diferencia entre la masa gravitacional
y la masa inercial, por lo que se tomarán indistintamente.
Partícula. El término partícula suele referirse a un objeto cuyo tamaño se reduce a un punto.
Cuerpo. El termino cuerpo suele referirse a un sistema de partículas que forman un objeto de tamaño apreciable. Sin embargo el criterio del tamaño es relativo, por lo cual los términos cuerpo y partícula se pueden aplicar al mismo objeto si es que la masa no se toma en cuenta en el análisis.
|
Sistema |
Longitud |
Tiempo |
Fuerza |
Masa |
|
Gravitacional Inglés |
pie (pie) |
segundo (seg, s) |
libra fuerza, lb, pound |
slug
|
|
Gravitacional Métrico técnico. |
metro (m) |
seg |
kilogramo fuerza (kgf) |
utm
|
|
Métrico absoluto CGS |
centímetro (cm) |
seg |
dina
|
gramo gr |
|
Métrico absoluto MKS |
metro (m) |
seg |
newton
|
kilogramo kg |
i el
coeficiente cinético de rozamiento entre las llantas de un automóvil y el
pavimento seco es de
,
determinar la distancia mínima en la cual el auto puede detenerse con una
velocidad inicial de
.
Paso 1. Fuerza
de rozamiento :
; donde
es
el coeficinete dinámico de rozamiento y N es la fuerza normal, esto es, la
reacción de la superficie de apoyo sobre el auto, que es igual en este caso al
peso del auto por considerarse una superficie de apoyo horizontal. Por lo que
; siendo m la masa del auto.
Paso 2.
Aplicando la segunda ley de Newton:
; sustituyendo a F por la fuerza de rozamiento:
; como
,
se tiene:
; simplificando:
despejando y
sustituyendo valores se tiene:
Paso 3. Para
calcular la distancia en la cual el auto se detiene, se utiliza la fórmula que
corresponde a los datos :
;
despejando y
sustituyendo:
Resp.
,
baja por una pendiente que forma un ángulo de 300 con la horizontal,
al aplicar los frenos el coeficiente de rozamiento entre las llantas y el
asfalto es de 0.8. Calcular la distancia que recorre hasta detenerse.
Paso 1.
Aplicando la segunda ley de Newton y considerando positivas las fuerzas en el
sentido del movimiento:
; sustituyendo de acuerdo al diagrama de cuerpo libre de la figura:
; como la fuerza de rozamiento está expresada por
; sustituyendo :
; eliminando la masa:
; sustituyendo los valores proporcionados:
con lo cual se obtiene
que la aceleración es de
Paso 2. La distancia en la cual se detiene, se obtiene sustituyendo los datos en la relación:
; con lo cual resulta
Resp.
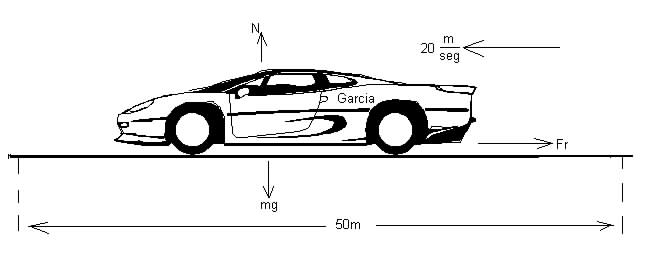
PROBLEMA 3.3.3. Un auto lleva una velocidad
de
en
el instante en que aplica los frenos en forma constante, y recorre 50m hasta
llegar al reposo. Determinar: a) el tiempo empleado en detenerse; b) el
coeficiente cinético de rozamiento entre las llantas y el asfalto.
Paso 1. Con los datos proporcionados, calcular la desaceleración:
; despejando y sustituyendo:
.
Paso 2. Con la
aceleración obtenida, se calcula ahora el tiempo que tarda en detenerse:
;
despejando y sustituyendo
valores:
Resp.
Paso 3. Para calcular el coeficiente de rozamiento dinámico, se utiliza la segunda ley de Newton:
siendo
en este caso
, por ser la única fuerza, la fuerza de rozamiento, la que se opone al
movimiento; sustituyendo
se
obtiene:
; la fuerza normal N es igual al peso del auto por estar sobre una superficie
horizontal; por lo que sustituyendo:
; quedando:
;
por lo que el valor del coeficiente de rozamiento, es
Resp.
.
Si el coeficiente cinético de rozamiento entre las superficies de contacto es de
0.2, determinar: a) la velocidad del paquete cuando se ha deslizado 5m; b) la
distancia que recorre el paquete hasta llegar al reposo.
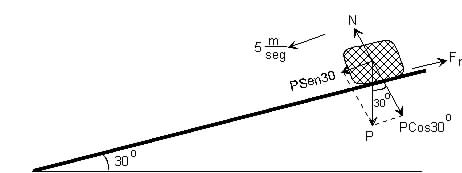
Paso 1. Aplicando la segunda ley de Newton y considerando positivas las
fuerzas en el sentido
del movimiento:
;
sustituyendo de acuardo con
el diagrama de cuerpo
libre de la figura, y sabiendo que
;
siendo P el peso del paquete:
; sustituír en esta expresión la relación
:
;
eliminando a P :
;
despejando la aceleración y sustituyendo valores:
Se
observa que no es necesario conocer el peso del paquete. Sustituyendo valores:
Paso 2. Conociendo la aceleración, calculamos la velocidad que tendrá el paquete cuando haya descendido 5m a lo largo del plano inclinado:
; sustituyendo valores:
siendo la velocidad
Resp.
Paso 3. La distancia que ecorre el paquete hasta llegar a detenerse:
;
despejando y sustituyendo valores:
Resp.
con respecto a la horizontal, con una velocidad constante de
.
¿Cuál será la aceleración del camión al llegar al plano horizontal de la
carretera?
Paso 1. Como la velocidad se mantiene constante en el plano inclinado,
entonces las únicas dos fuerzas que intervienen son:
estas dos fuerzas son iguales por lo
que la velocidad se mantiene constante; como se desconoce el coeficiente de
rozamiento, en lugar de la fuerza de rozamiento utilizaremos su equivalente que
es la fuerza
componente del peso del camión
.
Paso 2. En el instante en que el camión llega al camino horizontal :
; por lo que la aceleración es:
;
Resp.
,
se aplica una fuerza F al cable para detener al collarín. Determinar la magnitud
de la fuerza F si el collarín alcanza a recorrer 2m sobre la barra.
Paso 1. Aplicando la segunada ley de Newton y tomando en cuanta el diagrama
de cuerpo libre de la figura, se consideran positivas las fuerzas en el sentido del
movimiento:
;
Paso 2. De acuerdo con los datos, la aceleración del collarín se determina con la
relación:
;
sustituyendo los valores y despejando la aceleración:
;
Paso 3.
Sustituyendo los valores y sabiendo que la masa del collarín es
;
tenemos:
.
Resp.
