Práctica 5: Filtrado óptimo: Filtro de Wiener

(Para una buena introducción al filtro de Wiener, leer el siguiente documento: wiener.pdf )

Abre MATLAB.

Generaremos un filtro de orden 15.

P=15;

La señal deseada (señal de referencia) es una sinusoide de frecuencia 0.45 y 200 muestras.

N=200;
k=1:N;
w0=0.45;
d=sin(w0*k)'; %Senal deseada

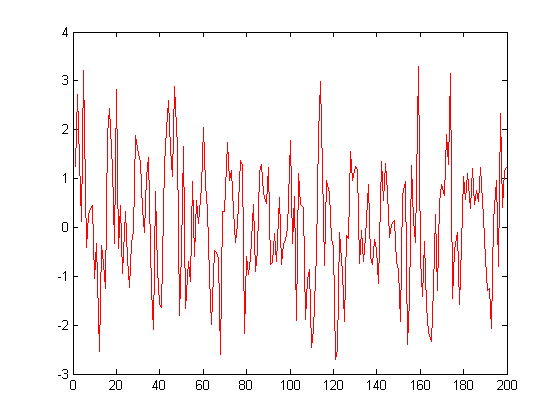
La señal a tratar es la señal deseada con un ruido blanco de distribución normal, varianza 1.

eps=1;
n=eps*randn(N,1);
x=d+n;

plot(x,'r');
%hold on;
%plot(d)
%hold off;
pause;

Sabemos de teoría que las ecuaciones de Wiener-Hopf modelan el sistema:

Calculamos la matriz R y el vector p y le decimos a Matlab que resuelva w de la ecuación. El operador "\" resuelve la ecuación de mínimos cuadrados. Es mucho más conveniente que calcular , ya que nadie nos asegura que la matriz de autocorrelación tenga inversa.

r=xcorr(x);
R=toeplitz(r(N:N+P-1));

ptemp=xcorr(x,d);
p=ptemp(N:N+P-1);

w=R\p

w =

0.1208
0.1070
0.0905
0.0416
-0.0104
-0.0574
-0.0774
-0.0922
-0.0831
-0.0703
-0.0269
0.0172
0.0613
0.0723
0.0783

Estos son los coeficientes que mejor filtran el ruido de la señal . Obviamente, la respuesta que te dará es diferente, ya que no estamos utilizando la matriz de autocorrelación real, sino una estimación en base a las muestras de que disponemos, que cambian cada vez que creamos la señal x al tener una componente aleatoria.

Vamos a ver cómo queda la señal después de filtrarla con nuestro filtro recién calculado, y lo compararemos con la señal deseada.

xrec=filter(w,1,x);

%plot(x,'r');
%hold on;
plot(xrec);
hold on;
plot(d,'g');
hold off;

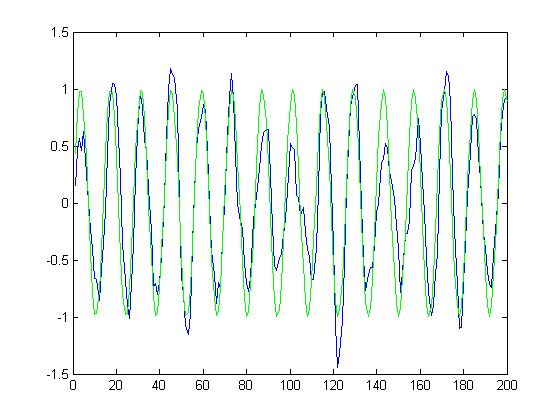
No está mal, comparándolo con la señal original. Para entender el tipo de filtrado que realiza el filtro de Wiener, vamos a ver la respuesta frecuencial del filtro frente al espectro de la señal que hemos recibido:

X=abs(fft(x,1024));
W=abs(fft(w,1024));

plot(X./max(X));
hold on;
plot(W./max(W),'r');
hold off;

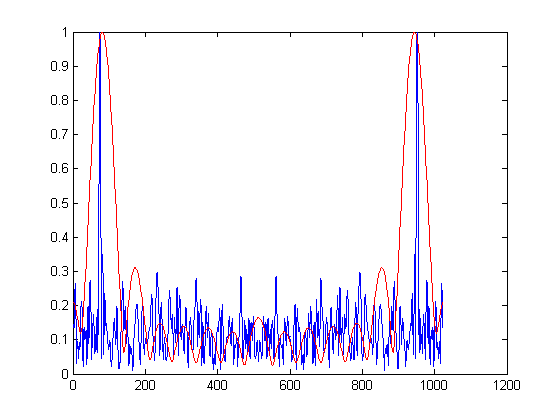
Si vemos el espectro de la señal después de filtrarla, y la comparamos con la señal deseada, vemos que realmente el filtro ha hecho un buen trabajo.

D=abs(fft(d,1024));
Xrec=abs(fft(xrec,1024));

plot(D,'g');
hold on;
plot(Xrec);
hold off;

Prueba variaciones de los parámetros de la señal y del filtro y describe cómo cambian los efectos del filtrado: prueba diferentes órdenes (P=6, 50 y 200), diferentes números de muestras (N=25 y 1000), diferentes frecuencias (w0=0.2 y 1.0) y diferentes varianzas (eps=0.25 y 5).

Comprueba el efecto de añadir un offset de 0.5 al ruido.

eps=1;
n=eps*randn(N,1)+0.5;

Volver a Índice de prácticas