
Questa pagina è la continuazione della prima pagina sulle aree e volumi; per capirla dovete leggere quella precedente. In questa uso dei metodi più sofisticati e tratto casi più specifici.

 (a2+b2)
(a2+b2) (a2+a2)
(a2+a2) (1*a2+1a2)
(1*a2+1a2) ((1+1)a2)
((1+1)a2) (2a2)
(2a2) 2*(a2)1/2
2*(a2)1/2 2*a2(1/2)
2*a2(1/2) 2*a1
2*a1 2*a
2*a 2*a
2*a 2*a=d //(
2*a=d //( 2)
2) 2*(1/
2*(1/ 2)a=d/
2)a=d/ 2
2 2
2 2
2 2*1
2*1 2)
2) 2*(1/
2*(1/ 2)
2) 2*(1/
2*(1/ 2)2
2)2 2*(12/(21/2)2)
2*(12/(21/2)2) 2*(1/2(1/2)2)
2*(1/2(1/2)2) 2*(1/21)
2*(1/21) 2*(1/2)
2*(1/2) 2/2)d
2/2)d 2/2)d)2
2/2)d)2 2/2)2d2
2/2)2d2 2)2
2)2 2/2)d
2/2)d
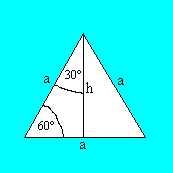
 (a2-(a/2)2)
(a2-(a/2)2) (a2-a2/22)
(a2-a2/22) (a2-a2/22)
(a2-a2/22) (a21-a2/4)
(a21-a2/4) (a24(1/4)-a2/4)
(a24(1/4)-a2/4) ((a24)/4-a2/4)
((a24)/4-a2/4) ((a24-a2)/4)
((a24-a2)/4) ((4a2-1a2)/4)
((4a2-1a2)/4) (((4-1)a2)/4)
(((4-1)a2)/4) (3a2(1/4))
(3a2(1/4)) 3(a2)1/2
3(a2)1/2 (1/4)
(1/4) 3(
3( 1/
1/ 4a2(1/2)
4a2(1/2) 3(1/2)a1
3(1/2)a1 3/2)a
3/2)a 3/2)a(1/2)
3/2)a(1/2) 3(1/2)a2
3(1/2)a2 3*a2
3*a2 3*a2
3*a2 3(1/4)a2
3(1/4)a2 3/4)a2
3/4)a2 3/2)a
3/2)a 3/4)a2
3/4)a2 3/4)a2
3/4)a2 3*a2
3*a2 3*a2
3*a2 3*a2
3*a2 3*a2
3*a2 3*a2
3*a2 3*a2
3*a2 3*a2
3*a2 3*a2
3*a2 3*a2
3*a2
 /(360°)*a (a espresso in gradi)
/(360°)*a (a espresso in gradi) /(2
/(2 )*a (a espresso in radianti)
)*a (a espresso in radianti) /2/
/2/ *a
*a (1/2)(1/
(1/2)(1/ )*a
)*a /
/ )(1/2)*a
)(1/2)*a
 (a2+b2)
(a2+b2) (d12+c2)
(d12+c2) (
( (a2+b2)2+c2)
(a2+b2)2+c2) (((a2+b2)1/2)2+c2)
(((a2+b2)1/2)2+c2) ((a2+b2)(1/2)2+c2)
((a2+b2)(1/2)2+c2) ((a2+b2)1+c2)
((a2+b2)1+c2) (a2+b2+c2)
(a2+b2+c2) (a2+b2+c2)
(a2+b2+c2) (a2+a2+a2)
(a2+a2+a2) (1a2+1a2+1a2)
(1a2+1a2+1a2) ((1+1+1)a2)
((1+1+1)a2) (3a2)
(3a2) 3*(a2)1/2
3*(a2)1/2 3*a2(1/2)
3*a2(1/2) 3*a1
3*a1 3*a
3*a 3*a
3*a 3*a=d //(
3*a=d //( 3)
3) 3(1/
3(1/ 3)a=d/
3)a=d/ 3
3 3
3 3
3 3*1
3*1 3)
3) 3*(1/
3*(1/ 3)
3) 3*(1/
3*(1/ 3)2
3)2 3*(12/(31/2)2)
3*(12/(31/2)2) 3*(1/3(1/2)2)
3*(1/3(1/2)2) 3*(1/31)
3*(1/31) 3*(1/3)
3*(1/3) 3/3)d
3/3)d 3)3
3)3 3/3)d
3/3)d , possiamo scrivere:
, possiamo scrivere: h
h
 , possiamo scrivere:
, possiamo scrivere: h/3
h/3
 h/3.
h/3. - immaginiamo il cerchio che ha per raggio il lato del quadrato (qui l' unica cosa da sapere a memoria è
- immaginiamo il cerchio che ha per raggio il lato del quadrato (qui l' unica cosa da sapere a memoria è  )
) h - immaginiamo il cilindro che ha per base il cerchio
h - immaginiamo il cilindro che ha per base il cerchio h/3 - immaginiamo di tagliare il cilindro di traverso tutto intorno fino ad ottenere il cono
h/3 - immaginiamo di tagliare il cilindro di traverso tutto intorno fino ad ottenere il cono



