Questa pagina è la continuazione della prima pagina sui perimetri e le superfici dei solidi; per capirla dovete leggere quella precedente. In questa tratto casi più specifici.


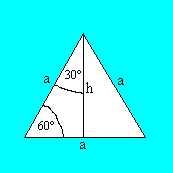
 /(360°)*a (a espresso in gradi)
/(360°)*a (a espresso in gradi) /(360°)*a
/(360°)*a /(360°)*a)
/(360°)*a) /(360°)*a)
/(360°)*a) /(360°)*a)
/(360°)*a) /(360°)*a) (a espresso in gradi)
/(360°)*a) (a espresso in gradi) /(2
/(2 )*a)
)*a) /2/
/2/ *a)
*a) (1/2)(1/
(1/2)(1/ )*a)
)*a) /
/ )(1/2)a)
)(1/2)a)
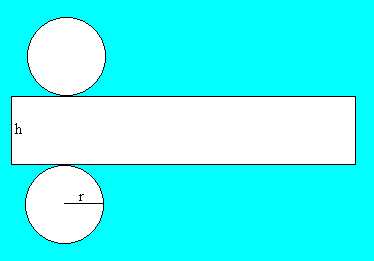
 e la sua area è uguale ad r2
e la sua area è uguale ad r2 , possiamo scrivere:
, possiamo scrivere: h+2r2
h+2r2
 h+2rr
h+2rr
 (h+r)
(h+r) (h+r)
(h+r) (h2+(b/2)2) ed h2=
(h2+(b/2)2) ed h2= (h2+(a/2)2) (e con un po' di calcoli h1=
(h2+(a/2)2) (e con un po' di calcoli h1= (h2+b2/4) e h2=
(h2+b2/4) e h2= (h2+a2/4)) possiamo scrivere:
(h2+a2/4)) possiamo scrivere: (h2+b2/4)+b
(h2+b2/4)+b (h2+a2/4)+ab
(h2+a2/4)+ab (h2+b2/4)+b
(h2+b2/4)+b (h2+a2/4)+ab
(h2+a2/4)+ab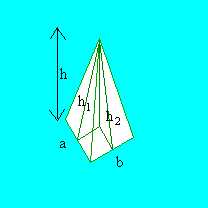

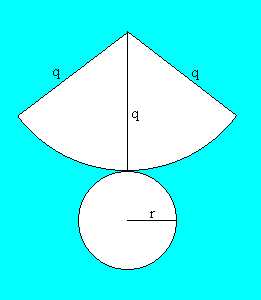
 e la sua area è uguale ad r2
e la sua area è uguale ad r2 e q=
e q= (r2+h2) (per il teorema di Pitagora), possiamo scrivere:
(r2+h2) (per il teorema di Pitagora), possiamo scrivere: q/2+r2
q/2+r2

 (r2+h2)/2+r2
(r2+h2)/2+r2

 (r2+h2)+rr
(r2+h2)+rr
 ((2/2)
((2/2) (r2+h2)+r)
(r2+h2)+r) (1
(1 (r2+h2)+r)
(r2+h2)+r) (
( (r2+h2)+r)
(r2+h2)+r) (
( (r2+h2)+r)
(r2+h2)+r)



