在當代,數學與邏輯學相互滲透,產生了多種交叉學科,「計算理論」(Computation Theory)就是這眾多學科
之一。「計算理論」不僅是「電腦科學」(Computer Science)的基礎理論,而且也涉及到數學和邏輯學的基礎
問題。在語言學方面,Chomsky把「計算理論」中有關「自動機」的理論應用於句法研究,實現了「喬姆斯基革
命」(Chomskyan Revolution)。此後語言學便廣泛採用數理邏輯工具,相繼形成「形式語言學」(Formal
Linguistics)、「計算語言學」(Computational Linguistics)等學科。
廣義量詞理論作為現代數理邏輯的引申和語言學的分支學科,當然也從「計算理論」中汲取很多有用的東西。
本章將介紹「計算理論」的兩大分支理論:「可計算性理論」(Computability Theory)和「計算複雜性理論」
(Computational Complexity Theory)在量詞上的應用。由於以上學科涉及艱深的理論,限於筆者的水平,本章
只能介紹皮毛和片面的知識。對於部分定理,本章只提供其內容及例證而略去有關證明。
早在電腦面世前,「計算理論」便已建構了多種「自動機」(Automaton)的模型,成為日後電腦的理論基礎。抽
象地說,一個「自動機」由一個「輸入字母表」(Input Alphabet)(以下記作Σ)、一組「狀態」(State)
(以下記作S)、一個「轉移函數」(Transition Function)(以下記作F)以及其他附加元件(詳見下文)組成,其中
Σ和S為有限集合。我們把由Σ中字母組成的序列稱為「字符串」(String),例如設Σ = {a,
b},那麼"abbab"便是一個可能的「字符串」。為方便下文的討論,我們把不含任何字母的空序列也視為「字符
串」,稱為「空字符串」(Empty String)(以下記作ε)。把一個「非空字符串」輸入一個「自動機」後
,該「自動機」的任務就是識別(Recognize)這個「字符串」是否滿足某些性質。我們把某「自動機」所能識別
的所有「字符串」稱為與該「自動機」相關的「形式語言」(Formal Language),每一種「自動機」都有一種相
關「形式語言」。
「自動機」識別「形式語言」的方法是首先把「自動機」設定於「起始狀態」(Start State)(以下記作
s0),然後把「自動機」的當前「狀態」、「字符串」中當前讀取的字母以及其他資料輸入「轉移
函數」F,由F確定「自動機」接著轉移至甚麼狀態以及採取甚麼行動。當「自動機」運行至某一步,滿足停機
條件,且處於「接受狀態」(Accept State)(「接受狀態」可以不只一個,故以下記作集合
Saccept)時,輸入的「字符串」就被識別,屬於與該「自動機」相關的「形式語言」。以下簡介三
種最基本的「自動機」。
最簡單的「自動機」稱為「有限自動機」(Finite Automaton)。「有限自動機」可以形式化地表達為 五元組(S, Σ, F, s0, Saccept),其中F是類型為
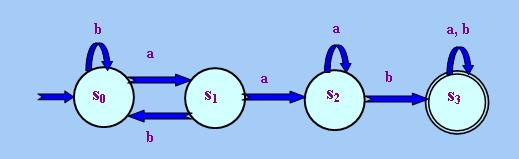
的函數,即輸入一個「狀態」和「字母」後,F便會輸出另一個「狀態」。「計算理論」使用劃一的圖示法來代 表「有限自動機」,例見下圖(以下把這個「自動機」稱為A1):

在上圖中,Σ = {a, b},S則由各個圓圈組成,即S = {s0, s1,
s2, s3}。圓圈之間箭頭上的字母則表達F的內容,其中箭頭的起點和箭頭上的字母為F
的輸入值,箭頭的終點則是F的輸出值。例如根據上圖,有F(s0, a) = s1,
F(s0, b) = s0等。沒有起點的箭頭所指著的圓圈代表s0,雙層圓圈則代
表Saccept的成員,即Saccept = {s3}。
A1所能識別的「形式語言」L1就是所有由字母"a"和"b"構成且包含"aab"的字符串,例
如"aaaaba"、"abaaba"等,理由如下:「自動機」從s0出發,只要讀取一個"b",它仍停留在
s0中,直至讀取一個"a"才轉移至s1。接著如果它讀取另一個"a",它便轉移至
s2,否則返回s0。如果在s2中它讀取"a",這個"a"是一連串"a"中的一個
,因此它仍停留在s2中。如果在s2中它讀取"b",這代表輸入的字符串包含"aab",因
此它便轉移至s3。此後,「自動機」讀取任何字母都會停留在s3中,直至讀取完最後
一個字母為止。
接著定義一種「形式語言」-「正則語言」(Regular Language)(以下記作RL),這是指可以由「
正則表達式」(Regular Expression)定義的字符串集合,「正則表達式」是一種簡化的集合表達法,有簡
單和複合兩種形式,簡單形式可以表現為Φ、ε或x,其中x ∈ Σ (這裡的ε或x
是{ε}或{x}的簡寫);複合形式則是由若干個字符串集合經「并」(Union)、「串接」(Concatenation)
和「克萊尼星號」(Kleene Star)等運算構成,以下是上述運算的定義:設A和B為字符串集合,那麼
(1)「并」運算:A ∪ B = {x: x ∈ A ∨ x ∈ B}
(2)「串接」運算:AB = {xy: x ∈ A ∧ x ∈ B}
(3)「克萊尼星號」運算:A* = {x1x2...xk: k ≥ 0 ∧
x1, x2 ... xk ∈ A}
舉例說,前述的「形式語言」L1是由字母"a"和"b"構成且包含"aab"的字符串組成的集合,因此
L1可以由以下「正則表達式」定義:
在上式中,aab是{a}{a}{b}的簡寫,即三個字符串集合的「串接」,相等於{aab}。(a ∪ b)則是{a} ∪
{b}的簡寫,即兩個字符串集合的「并」,相等於{a, b};而(a ∪ b)*則等於{ε, a, b, aa, ab,
ba, bb, aaa, ...},容易看到上式是L1的正確表達。
在「計算理論」中,我們有以下定理(證明從略):
定理1:「形式語言」L可被某「有限自動機」識別當且僅當L是一種「正則語言」。
前面說過,「有限自動機」A1能識別「形式語言」L1,而在上面筆者指出
L1可用「正則表達式」定義,由此驗證了「定理1」。
在本小節,筆者要介紹識別能力比「有限自動機」較強的「下推自動機」(Pushdown Automaton)。「 下推自動機」與「有限自動機」的區別在於,前者比後者多了一個元件-「棧」(Stack),可供「下推自動機」 用來存取文字資料,可寫入「棧」的文字資料本身構成一個「棧字母表」(Stack Alphabet)(以下記作Γ) 。「棧」的工作原理是「後進先出」,即最後寫入「棧」中的字母會存入「棧」的最頂端,並會最先被取出。 「下推自動機」可以形式化地表達為六元組(S, Σ, Γ, F, s0, Saccept) ,其中F是類型為
的函數。在上式中,Σε = Σ ∪ {ε},
Γε = Γ ∪ {ε},Power(S ×
Γε)則代表由有序對(s, x)組成的集合,其中s ∈ S,x ∈
Γε。
函數(1)與(2)有兩個重要區別。首先,在輸入方面,(2)除了多了一個輸入項外,它的第二和第三輸入項可以是
「空字符串」ε,這即是說「下推自動機」可以在沒有讀取任何字母的情況下應用函數F。其次,在輸
出方面,(2)除了多了一個輸出項外,它的輸出被表達為一個集合而非元素,這即是說「下推自動機」的輸出並
不唯一。總括而言,函數(1)只有在讀取某一字母後才會輸出唯一確定的值;(2)則可在沒有讀取任何字母的情
況下提供輸出值,而且這個值並不唯一。
(1)與(2)代表兩類很不同的「自動機」,前者稱為「確定型自動機」(Deterministic Automaton),後者則稱為
「非確定型自動機」(Non-Deterministic Automaton),分別以前述的「有限自動機」和「下推自動機」為代表
(註1)。由於「非確定型自動機」的「轉移函數」輸出值不唯一,對於某一輸入字符串,它有多個可能計算結果
,我們規定只要其中一個計算結果是處於「接受狀態」,輸入字符串便算是被識別。
「計算理論」也使用劃一的圖示法來代表「下推自動機」,例見下圖(以下把這個「自動機」稱為
A2):
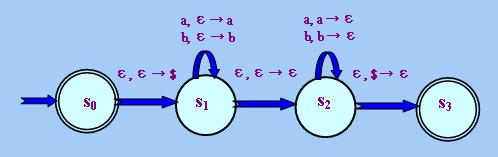
在上圖中,Σ = {a, b},Γ = {a, b, $},其中$是用來標記「棧」是空的。Saccept
= {s0, s3},即s0既是「起始狀態」,又屬於「接受狀態」,因此
A2接受ε。箭頭上的文字是F輸入/輸出值的簡化記法,例如根據上圖,有
F(s0, ε, ε) = {(s1, $)}。請注意在上圖中"a, ε →
a"與"a, a → ε"的區別,前者的意思是若輸入字符串當前讀取的字母是"a",則不論「棧」頂當
前的字母是甚麼,都把"a"寫入「棧」中;後者的意思是若輸入字符串當前讀取的字母是"a",而「棧」頂當前
的字母也是"a",則用ε取代「棧」頂的"a",亦即把「棧」頂的"a"擦去。
A2所能識別的「形式語言」L2就是所有由字母"a"和"b"構成且形如WWR的
字符串,其中WR代表把W中的字母倒轉次序而得的字符串,例如"bbaabb"、"abbbba"等,理由如下
:A2首先把"$"寫入「棧」中,然後轉移至狀態s1。在這個狀態中,「自動機」把讀入
的字母"a"或"b"依次寫入「棧」中,直至某一時刻,「自動機」便轉移至狀態s2 (註2)。在這個狀
態中,「自動機」把輸入字符串餘下部分的當前字母逐一與「棧」頂端的當前字母核對,兩者相同便把「棧」
頂端的當前字母擦去,兩者不同則不作任何事(上圖中無定義)。直至最後,若輸入字符串已讀取完結而「棧」
中只餘下字母"$",這代表輸入字符串具有WWR的形式,「自動機」便即轉移至狀態s3
,否則停留於s2。
接著定義「上下文無關語言」(Context Free Language)(以下記作CFL),這是指可用「上下文無
關語法」(Context Free Grammar)生成的字符串集合。「上下文無關語法」可以定義為四元組(N, T, R,
s),其中N是「非終端符號」(Non-Terminal Symbol)集合、T是「終端符號」(Terminal Symbol)集合、s
∈ N是「起始符號」(Start Symbol)、R則是由「代換規則」(Substitution Rule)組成的集合,「代換規
則」具有x → Y的形式,其中x ∈ N,Y ∈ (N ∪ T)*。這些規則的作用是把字符串中所含的
x代換為Y。
使用上述語法生成字符串的步驟是,首先寫出「起始符號」s,然後應用適當的「代換規則」把s代換為另一字
符串,並繼續進行這種代換,直至字符串只包含「終端符號」為止。以前述的L2為例,它便可用語
法(N, T, R, s)生成,其中N = {s},T = {a, b},而R則包含以下規則:
舉例說,字符串"bbaabb"便可按以下步驟生成:
容易看到L2中的其他字符串也可用上述語法生成。
在「計算理論」中,我們有以下定理(證明從略):
定理2:「形式語言」L可被某「下推自動機」識別當且僅當L是一種「上下文無關語言」。
前面說過,「下推自動機」A2能識別L2,而在上面筆者指出L2可用「上下
文無關語法」生成,由此驗證了「定理2」。
「圖靈機」(Turing Machine)是識別能力最強的「自動機」,我們現在使用的電腦就是以「圖靈機」 作為理論基礎。「圖靈機」的特點是有一條分成無限多個「格」(Cell)的一維「紙帶」(Tape)和一個每次可向 左或右移動一格的「讀寫頭」(Head)。輸入字符串就寫在「紙帶」上,我們並假設「紙帶」上的其他「格」都 有一個特殊的符號:Δ,代表「空白」。在開始計算時,「讀寫頭」被置於輸入字符串第一個字母所在的 「格」上。「讀寫頭」的作用是讀取紙帶上的字母,並可在紙帶上寫上字母或Δ(在某「格」上寫上 Δ等同於擦去該「格」上的字母)。可供「讀寫頭」寫上「紙帶」的字母構成一個「紙帶字母表」(Tape Alphabet)(以下記作Γ),Γ與Σ的關係為Σ ⊆ Γ − {Δ}。「 圖靈機」可以形式化地表達為七元組(S, Σ, Γ, F, s0, saccept, sreject),其中saccept和sreject分別代表(唯一一個的)「接受狀態」和 (唯一一個的)「拒絕狀態」,F是類型為(註3)
的函數。在上式中,L和R分別代表「向左移動一格」和「向右移動一格」。跟前兩種「自動機」的運作方式不
同,「圖靈機」不是以讀取完整個輸入字符串,而是以進入「接受/拒絕狀態」作為停機條件,所以不能保證
必能停機。因此把一個「圖靈機」不能識別的字符串輸入該機時,有兩種可能情況出現:它最終停於「拒絕狀
態」,或者進入「無窮迴圈」(Infinite Loop)而永不停機。
永不停機是一種不理想的情況,因為在輸入一個字符串後,當「圖靈機」尚未停機時,我們無法判斷「圖靈機」
最終會否接受該字符串。因此學者定義了「圖靈機」的一個次類:「全圖靈機」(Total Turing
Machine),而把一般的「圖靈機」稱為「偏圖靈機」(Partial Turing Machine)。「全圖靈機」的特
性是在輸入任何字符串後總會停於「接受/拒絕狀態」,我們把這種特性稱為「可判定性」(Decidability),
以區別於一般的「可識別性」(Recognizability)。相應地,與「圖靈機」相關的「形式語言」也分為兩種,我
們把可被「圖靈機」識別的語言稱為「遞歸可枚舉語言」(Recursively Enumerable Language)(記作
REL),而把可被「圖靈機」判定的語言稱為「遞歸語言」(Recursive Language)(記作RL)。由於「可
判定性」是比「可識別性」更嚴格的性質,我們有RL ⊂ REL。在本節我們將集中討論較一般的「偏圖靈機」
(儘管以下介紹的「圖靈機」實際都是「全圖靈機」),而在第3節我們將把焦點轉移至「全圖靈機」。
「計算理論」也使用劃一的圖示法來代表「圖靈機」,例見下圖(以下把這個「自動機」稱為A3):

在上圖中,Σ = {a, b, c},Γ = {a, b, c, $, Δ}。箭頭上的文字是F輸入/輸出值的簡化
記法,例如根據上圖,有F(s0, a) = (s1, $, R),意思是若當前狀態為
s0而且當前讀取的字母為"a",則「自動機」轉移至狀態s1,把紙帶上的"a"改為"$",
並把「讀寫頭」向右移一格。請注意為簡單起見,上圖沒有實際繪出指向sreject的箭頭,因為我
們可以規定,凡圖中沒有定義的輸入值,其輸出值的第一項一律為sreject,而第二和第三項則無
需註明,因為反正「自動機」將要停機,第二和第三項是甚麼都無關宏旨。根據此一規定,我們有
F(s0, b) = (sreject, ?, ?)。
A3所能識別的「形式語言」L3就是所有形如
"anbncn"的字符串,其中an代表n個連續的"a",n ≥ 0,
例如ε 、 "aabbcc"等,理由如下:「讀寫頭」從s0出發,若讀取"Δ",即代表輸入
字符串為ε,「讀寫頭」便即轉移至saccept並且停機。若讀取"a",則把這個"a"改為"$"
以作記認。接著「讀寫頭」在s1狀態下向右穿越整排"a",並在遇到"b"後進入s2。接
著「讀寫頭」向右穿越整排"b",並在遇到"c"後向左返回最後一個"b"的位置,把這個"b"改寫為"c",並進入
s4。接著「讀寫頭」向右穿越整排"c",並在遇到"Δ"後進入s5,這時「讀寫頭」
已到達輸入字符串的末端。接下來「讀寫頭」向左把兩個"c"擦掉,這實際等於把輸入字符串中的一個"b"和"c"
擦掉(因為「讀寫頭」曾在s3狀態下把一個"b"改寫為"c")。擦掉這兩個字母的目的是要檢查輸入字
符串中"b"和"c"的數目是否等於"a"的數目。接著「讀寫頭」在s7狀態下向左穿越所有"c"、"b"和
"a",直至遇到"$",然後進入s0,再從頭進行上述步驟。
接著定義「短語結構語言」(Phrase Structure Language)(以下記作PSL),這是指可用「短語結
構語法」(Phrase Structure Grammar)生成的字符串集合。「短語結構語法」的定義跟「上下文無關語法
」大致相同,唯一不同之處在於前者的「代換規則」具有X → Y的形式,其中X為包含至少一個「非終端符
號」的字符串,Y則同前。
以前述的L3為例,它可用語法(N, T, R, s)生成,其中N = {s, t, u, v},T = {a, b, c},而R則
包含以下規則:
舉例說,字符串"aabbcc"便可按以下步驟生成:
容易看到L3中的其他字符串也可用上述語法生成。
在「計算理論」中,我們有以下定理(證明從略):
定理3:「形式語言」L可被某「圖靈機」識別當且僅當L是一種「短語結構語言」,亦即REL = PSL。
前面說過,「圖靈機」A3能識別L3,而在上面筆者指出L3可用「短語結構
語法」生成,由此驗證了「定理3」。
至此筆者已介紹了三種「自動機」及其相關「形式語言」,這些「形式語言」之間具有以下包含關係(證明從略
)(註4):
定理4:RL ⊂ CFL ⊂ RL ⊂ PSL = REL
綜合運用以上定理,我們還可以推得「自動機」與「形式語言」之間的其他關係,例如由於所有「正則語言」
都是「短語結構語言」,根據「定理3」,我們知道每種「正則語言」都可被某「圖靈機」識別。
在「計算理論」中,「圖靈機」是計算能力最強的「自動機」,今天電腦所能進行的各種運算都能用「圖靈機」
進行。不過,「計算理論」亦發現一些連「圖靈機」也不能計算的問題,由於這些問題頗為抽象,而且跟量詞
關係不大,本文不予介紹。
van Benthem在Semantic Automata一文中提出用「自動機」表述量詞,從而把廣義量詞理論與「可計算 性理論」聯繫起來。為簡化討論,以下只考慮「有限論域邏輯限定詞」,即屬於LOG ∩ FIN的限定詞。要建 立這種限定詞與「自動機」之間的聯繫,我們首先要為量化句Q(A)(B)的語義模型「編碼」(Encoding),即把它 們轉化為字符串。設A和B為有限論域U上的集合,這兩個集合把U分割為下圖所示的四個互不重疊的區域:

但在LOG ∩ FIN下,我們只需考慮A − B和A ∩ B這兩個區域。因此Q(A)(B)的語義模型只需包含
A中元素的資料,這些元素要麼屬於A − B,要麼屬於A ∩ B。假設我們把A的元素按某個順序排成一
個序列,對於每個元素,我們按它是屬於A − B還是A ∩ B而把它編碼為"0"或"1",這樣我們便會得
到一個由字母"0"和"1"組成的字符串。舉例說,設在某語義模型下,A = {a, b, c, d, e},A − B =
{b, e},A ∩ B = {a, c, d},如果我們按abcde的順序排列A的元素,那麼上述語義模型便可編碼為字符串
"10110"。由於每個語義模型對應著一個字符串,使Q為真的語義模型集合便對應著一個字符串集合,即一個「
形式語言」LQ,這樣Q便對應著一個「自動機」AQ,這個AQ以
LQ作為其相關「形式語言」。我們把AQ這種「自動機」稱為「量詞自動機」
(Quantifier Automaton) (van Benthem稱為「語義自動機」Semantic Automaton)。
舉例說,以下兩個「有限自動機」便分別對應著"every"和"(at least 3)":

以上兩個「自動機」可分別識別由「正則表達式」"1*"和"0*10*10*1(0 ∪ 1)*"定義的「形式語言」,前者
的元素為只包含"1"的字符串,後者的元素為包含至少三個"1"的字符串。請注意以上兩個「自動機」具有
「排列不變性」(Permutation Invariance),即給定某一字符串,無論如何重排該字符串中的字母順序,
輸入「自動機」後都會得到相同的結果,因此雖然我們在上面假設以某一順序排列語義模型中的元素,這個順
序其實並無重要性,上述「排列不變性」正與本文所研究限定詞的「邏輯性」相協調。
根據限定詞「外部否定」、「內部否定」和「對偶」的定義(見《廣義量詞系列
:對偶性推理基礎》),我們可以從某限定詞的「有限自動機」推導出另一限定詞的「有限自動機」。設Q
為限定詞,AQ為其「有限自動機」。如果把AQ上的所有「接受狀態」和「非接受狀態」
對調,便可得到~Q的「有限自動機」A~Q;如果把AQ上的所有字母"0"和"1"對調,便可
得到Q~的「有限自動機」AQ~;如果把AQ上的所有「接受狀態」和「非接受狀態」對調
,並同時把所有字母"0"和"1"對調,便可得到Qd的「有限自動機」AQd。
舉例說,以下便是"(not every)"、"no"和"some"的「有限自動機」:

接著讓我們按照「自動機」的特性為限定詞分類。前面介紹的「量詞自動機」都具有「非循環性」
(Acyclicity),即不存在一條「循環路徑」(我們可以把「自動機」上的「狀態」看成區域,把箭頭看成區域之
間的通道)從一個「狀態」經其他「狀態」返回原來的「狀態」。從某個角度看,這類「自動機」是最簡單的「
量詞自動機」,我們有以下定理(以下把在某邏輯系統L下可定義的量詞的集合記作L-D):
定理5:限定詞Q ∈ FO-D當且僅當AQ是「非循環排列不變有限自動機」。
在上述定理中,FO代表「一階邏輯」。以下證明上述定理,由於以下的證明要用到「數字三角形」,讓我們重
溫「數字三角形」的一般結構:

首先設Q ∈ FO-D,根據《廣義量詞系列:量詞的邏輯性質》,Q的「 數字三角形」具有以下特徵:

在上圖中,存在一條「第2n對角線」使得在該「對角線」以下的「+/−」號分佈呈以下規律性:以[n,
n]為頂點的整個三角形同號;對[n, n]左面各個位置而言,該位置所在的「列」由該位置起向下全部同號;對
[n, n]右面各個位置而言,該位置所在的「行」由該位置起向下全部同號。
接著我們把上述「數字三角形」轉化為「有限自動機」,「數字三角形」上的位置可以轉化為「自動機」的「
狀態」,其中「+」號和「−」號分別對應著「接受狀態」和「非接受狀態」,[0, 0]位置則對應著「起
始狀態」。此外,我們還要加上一些代表「轉移函數」的箭頭。從「第0對角線」到「第2n − 1對角線」
,我們加上以下箭頭:從每一個位置[x, y]都有一個帶"0"的箭頭指向[x + 1, y],以及另一個帶"1"的箭頭指
向[x, y + 1]。請注意這些箭頭是語義模型的正確反映,例如設「自動機」當前正處於[x, y]位置,這代表「
自動機」至今已確定有x和y個元素分別屬於A − B和A ∩ B。「自動機」接著讀取一個字母,若這個
字母是"0",這表示A − B應有多一個元素,所以「自動機」應轉移至[x + 1, y]位置;若這個字母是"1"
,這表示A ∩ B應有多一個元素,所以「自動機」應轉移至[x, y + 1]位置。
理論上我們可以把上述加箭頭的方法應用於每條「對角線」,但由於「數字三角形」有無限多條「對角線」,
這樣我們將會得到一個「無限自動機」。為避免這個問題,我們可以利用上述「數字三角形」的特徵,在「第
2n對角線」上加上以下箭頭來代替「第2n對角線」以下的無限個箭頭:

請注意上述箭頭正確反映了「第2n對角線」以下「+/−」號的分佈,例如設「自動機」當前正處於[2n,
0]位置,並接著讀取一個字母。若這個字母是"0",「自動機」按理應轉移至[2n + 1, 0]位置,但由於[2n +
1, 0]與[2n, 0]同號,這實際等於把「自動機」停留在[2n, 0]位置;若這個字母是"1",「自動機」按理應轉
移至[2n, 1]位置,但由於[2n, 1]與[2n − 1, 1]同號,這實際等於把「自動機」轉移至[2n − 1,
1]位置。以上就是上圖所示箭頭的理據。
利用上述方法,我們便可以把Q轉化為一個「有限自動機」,這個「自動機」顯然具有「非循環性」和「排列不
變性」,而且它能識別一個字符串,當且僅當這個字符串所代表的語義模型使Q為真,亦即等於AQ
。至此我們證明了若Q ∈ FO-D,則AQ是「非循環排列不變有限自動機」。
以上面的「數字三角形」為例,我們可以把它轉化為以下「自動機」:

我們可以用一些字符串來驗證上述「自動機」是正確的,例如在上述「數字三角形」中,位置[3, 4]取「+」號
。如果我們把一個包含3個"0"和4個"1"的字符串(例如"0100111")輸入上述「自動機」,「自動機」最終將停留
於狀態[2, 2],而這正是一個「接受狀態」。
接著設有一個「非循環排列不變有限自動機」A4,對於A4的每個「接受狀態」而言,
只有有限種路徑從「起始狀態」轉移至該狀態,而這些路徑(亦即A4可識別的字符串)都可表達為由
"0" 、 "1" 、 "0*" 或"1*"經「串接」而形成的「正則表達式」,這些「正則表達式」都可表達為以下四類
「一階可定義限定詞」之一:
例如"0101101*"便可表達為"(exactly 3)(A)(~B) ∧ (at least 4)(A)(B)"。由於 A4只有有限個「接受狀態」,它所對應的限定詞Q等同於有限個「一階可定義限定詞」的析取,因 此Q ∈ FO-D。「定理4」至此得證。
上一小節討論的「排列不變有限自動機」都具有「非循環性」,現在如果我們放棄「非循環性」,所得「自動 機」的識別能力將會更高。舉例說,以下這個包含「兩狀態循環」的「自動機」便是對應"(an even number of)"的「自動機」:

請注意在上圖中,狀態s0和s1構成一個循環,而(an even number of)
~∈ FO-D。
我們還可以把上述「兩狀態循環」進一步推廣為「n狀態循環」,從而得到一些特殊的「量詞自動機」,例如
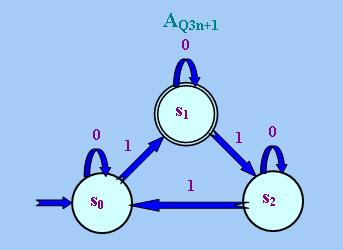
以上這個「自動機」AQ3n+1能識別所有由"0"和"1"組成且所含"1"的數目是一個被3除餘數為1的整 數(例如1、4、7等),因此它對應著以下限定詞:
請注意Q3n+1 ~∈ FO-D。雖然上述兩個限定詞都是「一階不可定義」的,但我們可以在「一階 邏輯」中加入以下<1>型「整除性量詞」(Divisibility Quantifier):
其中n為大於1的整數(註5),從而得到FO(D2, D3, ...),以下記作FO(DN) ,稱為「整除性邏輯」(Divisibility Logic)。請注意上述兩個限定詞在「整除性邏輯」下是可定義 的,舉例說,由於Q3n+1(A)(B)當且僅當從A ∩ B剔除一個元素後所得集合的基數可被3整除, 我們有
| Q3n+1(A)(B) | ⇔ ∃x (x ∈ A ∩ B ∧ D3({y: A ∩ B − {x}})) |
| ⇔ ∃x (A(x) ∧ B(x) ∧ D3y (A(y) ∧ B(y) ∧ y ≠ x)) |
從上述結果,我們可以猜想「n狀態循環」與Dn有一定聯繫。事實上,根據Mostowski的
Computational Semantics for monadic quantifiers一文,我們有以下定理(證明從略):
定理6:限定詞Q ∈ FO(DN)-D當且僅當AQ是「排列不變有限自動機」。
某些常用的限定詞(例如"most"以及很多「右比例限定詞」和「右補右比例限定詞」等)即使在「整除性 邏輯」下也是不可定義的,即不能被任何「排列不變有限自動機」識別。對於這些限定詞,我們要使用「排列 不變下推自動機」。舉例說,以下便是"most"所對應的「自動機」:
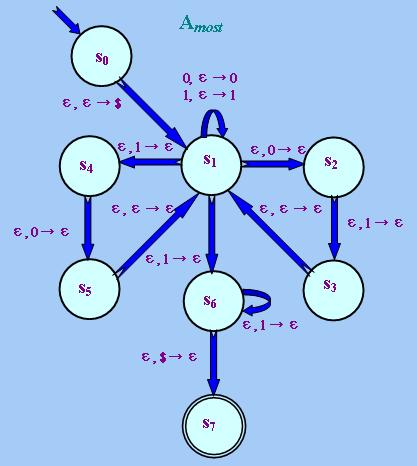
上述「自動機」能識別所有由"0"和"1"組成並且所含"1"的數目較"0"為多的字符串,其運作程序如下:開始時
首先把符號"$"寫入「棧」中以作記認,接著在狀態s1把讀取到的"0"和"1"依次寫入「棧」中。在
適當時候,「自動機」會進入狀態s2,把「棧」頂的一個"0"及緊接其下的一個"1"擦掉;或者進入
狀態s4,把「棧」頂的一個"1"及緊接其下的一個"0"擦掉,然後返回s1。上述操作的
作用是從「棧」中把相同數目的"0"和"1"擦去。如是者直到已讀取完所有字母後,如果「棧」中仍有未擦去的
"1",「自動機」便會進入狀態s6,把「棧」頂餘下的"1"全部擦去。這時如果「棧」頂的字母是
"$",「自動機」便會進入「接受狀態」s7。
在上述程序中,擦掉相鄰的一個"0"和一個"1"的操作是關鍵的步驟。可是,我們能否保證,所有能被
Amost識別的字符串都能進行上述操作?答案是肯定的,因為如果一個字符串所含"1"的數
目較"0"為多,即使該字符串包含一些連續的"0",這些"0"的左側或右側必有至少一個"1",我們可以先把這個
"1"與其鄰接的"0"擦去,這樣本來不與"1"相鄰的"0"早晚也會變成與"1"相鄰而被擦去。舉例說,設輸入字符串
是
當「自動機」讀取完首三個字母後,「棧」中所儲存的字母為"$001" (這裡最右的字母位於「棧」頂),這時「
自動機」可以先把「棧」頂的一個"1"和一個"0"擦掉。接著「自動機」繼續讀取兩個字母,使「棧」中所儲存
的字母為"$001",這時「自動機」又可以把「棧」頂的一個"1"和一個"0"擦掉。接著「自動機」再讀取一個"1"
,使「棧」中所儲存的字母為"$01",這時「自動機」又可以把「棧」頂的一個"1"和一個"0"擦掉。接著「自動
機」讀取最後一個"1",使「棧」中所儲存的字母為"$1"。接著當「自動機」把「棧」中所有"1"擦去後,發覺
僅餘下"$",進入「接受狀態」,由此可知輸入字符串屬於Amost所能識別的語言。
根據van Benthem,各種「右比例限定詞」、「右補右比例限定詞」以及前述的「整除性可定義限定詞」在一種
賦有「加法」的「一階邏輯」(以下稱為「加法邏輯」(Additive Logic),記作FO(+))是可定義的。
舉例說,"most"以及前述Q3n+1的真值條件乃分別建基於數值比較關係"<"和「模3同餘」
(Congruence Modulo 3)關係(在數學上我們把「x被3除餘數為1」記作x ≡ 1 (mod 3)),而這兩個關係可
以用「加法」定義如下(在以下定義中,x、y和n為自然數):
根據van Benthem,我們還有以下定理(證明從略):
定理7:限定詞Q ∈ FO(+)當且僅當AQ是「排列不變下推自動機」。
根據「定理7」,「排列不變下推自動機」所能識別的限定詞已包含最常用的限定詞,自然語言中是否有任何量 詞超出「排列不變下推自動機」的識別能力?筆者在2.1.3小節介紹了一個可識別「形式語言」L3 = {anbncn: n ≥ 0}的「圖靈機」A3,L3便超 出了「下推自動機」的識別能力。L3可被視為對應著以下「<13,1>型結構化量詞」:
為簡化討論,我們假設上式中的集合A、B和C兩兩互不相交,例如句子
中的"elderly"、"middle aged"和"youngsters"便可以表達為兩兩互不相交的集合。如何用「圖靈機」識別上
述量詞?由於上述量詞不是限定詞,我們需要採用另一種編碼方法。根據筆者在
《廣義量詞系列:量詞的普遍性質與操作》中討論的「結構化量詞的守恆
性」,上述量詞的語義模型只需包含集合A ∪ B ∪ C中元素的資料,但由於A、B和C兩兩互不相交,我
們可以按這些元素是屬於A ∩ D、B ∩ D、C ∩ D、A − D、B − D或C − D而把
它們編碼為"a"、"b"、"c"、"d"、"e"或"f",這樣我們便會得到一個由字母"a"至"f"組成的字符串。
接著我們用兩個「圖靈機」來模擬所需的「排列不變圖靈機」。首先,我們設計一個「圖靈機」A4
來對輸入字符串進行篩選和重新排序,A4首先檢查輸入字符串是否包含"a"至"f"以外的字母,然後
從頭到尾掃描輸入字符串三次,第一次把所有"d"、"e"、"f"刪去,第二次把所有"b"移至字符串的尾端,第三
次則把所有"c"移至字符串的尾端,這樣便把輸入字符串改寫為"aibjck"
的形式。接著,我們便可以用前述的A3來識別上述改寫了的字符串。
究竟是否存在連「排列不變圖靈機」也不能識別的量詞?這是一個艱深而抽象的問題,因此我們不能像「定理5
-7」那樣列出「排列不變圖靈機」所對應的量詞類別。此外,在自然語言中並非所有量詞都具有「邏輯性」,
例如"John's"等,而在「可計算性理論」中也並非所有「自動機」都具有「排列不變性」。有關一般量
詞與一般「自動機」的對應關係,還有待學者研究。
「可計算性理論」研究一種「形式語言」是否能被某種「自動機」計算(註6)的問題,而「計算複雜性理論」則 研究「自動機」計算「形式語言」的效率。為比較效率,「計算複雜性理論」採用一種特殊的符號。設f(n)和 g(n)為把自然數映射為非負實數的函數,那麼我們有
當且僅當存在自然數c和m,使得對所有大於或等於m的n,都有f(n) ≤ cg(n),在實際應用中,通常把g(n)寫 成系數為1的單項函數。以f(n) = 5n3 + 2n2 + 22n + 6為例,容易驗證當n ≥ 10 時,5n3 + 2n2 + 22n + 6 ≤ 6n3,因此我們有
上述定義其實是把數學表達式按大小排成層級,例如屬O(n2)的函數顯然不會大於屬 O(n3)的函數。我們有以下層級:
接著我們可以用上述概念來比較「自動機」的效率,這裡的「自動機」一般為「全圖靈機」,而效率則用計算
所需耗用的資源來量度,耗用的資源越少,「自動機」的效率便越高。這裡的資源分為時間資源和空間資源兩
種,時間資源一般用「全圖靈機」在「紙帶」上所需移動的總步數來量度,空間資源則用「全圖靈機」在整個
計算過程中所需用到「紙帶」的最大「格」數來量度。我們把以上兩個數目表達為輸入字符串長度n的函數。請
注意對於空間資源來說,「計算複雜性理論」一般以前述「全圖靈機」的一種變體-「多帶圖靈機」
(Multitape Turing Machine)作為基準,這種「圖靈機」含有多條「紙帶」,其中一條是用來儲存輸入字符串
、只供讀取的「輸入紙帶」(Input Tape),其餘的是用來進行計算、可供讀和寫的「工作紙帶」(Work Tape)。
在量度空間資源時,我們只計算所需用到「工作紙帶」的最大「格」數。因此之故,「多帶圖靈機」所用的空
間資源有可能少於輸入字符串的長度。
以2.1.3小節計算L3 = {anbncn: n ≥ 0}的「確定型全圖
靈機」A3為例,設輸入字符串w的長度為n,讓我們粗略地估計它識別w所需移動的總步數。
A3的運作方式是,只要w中仍有字母,它便重覆進行以下步驟:從頭向右掃描w一次,把最前的一個
"a"改寫成"$",並把一個"b"和一個"c"擦掉,然後從尾向左返回最後的"$"位置。粗略地看,每次掃描共需移動
約2n步(從頭向右 + 從尾向左);由於每次進行上述掃描都會使w減去三個字母,上述掃描共需進行n / 3次,因
此A3所需移動的總步數約為2n(n / 3) = O(n2),我們把O(n2)稱為
A3的「時間複雜性」(Time Complexity)。
類似地,我們也可以分析A3的「空間複雜性」(Space Complexity)。由於A3是普通的
「全圖靈機」,它的「輸入紙帶」也就是它的「工作紙帶」,所以我們要考慮所用到整條「紙帶」的最大「格」
數。由於A3自始至終最多只用到「紙帶」上的n個「格」,而n = O(n),所以其「空間複雜性」就
是O(n)。
我們可以按「確定型全圖靈機」的「時間/空間複雜性」把「形式語言」分為各個「複雜性類別」(Complexity
Class)。具體地說,我們把「時間/空間複雜性」為O(g(n))的「確定型全圖靈機」所能計算的「形式語言」組
成集合TIME(g(n))或SPACE(g(n)),例如根據上面的討論,我們有
{anbncn: n ≥ 0} ∈ TIME(n2) ∩ SPACE(n)。
除了「確定型全圖靈機」外,我們還可按「非確定型全圖靈機」的「時間/空間複雜性」把「形式語言」分類
。請注意「確定型全圖靈機」和「非確定型全圖靈機」儘管在計算能力上等價,但它們在「計算複雜性」方面
卻可能有不同的表現。類似上段的定義,我們可以定義集合NTIME(g(n))或NSPACE(g(n)),其中"N"代表這些語
言是被「非確定型全圖靈機」計算。
我們還可以把上述「複雜性類別」按其函數類型組成更大的類別,定義如下:
| 名稱 | 代號 | 定義 |
|---|---|---|
在上表中,"LOG"、"P"、"EXP"和"N"分別代表「對數函數」(Logarithmic Function)、「多項式函數」
(Polynomial Function)、「指數函數」(Exponential Function)和「非確定型」(Non-Deterministic)。
上表中的類別構成以下層級關係(證明從略):
定理8:LOGSPACE ⊆ NLOGSPACE ⊆ PTIME ⊆ NPTIME ⊆ PSPACE = NPSPACE
⊆ EXPTIME ⊆ NEXPTIME
「定理8」的層級基本上按照「對數函數」、「多項式函數」和「指數函數」的次序遞增。在「計算複雜性理論
」中,一般認為EXPTIME或以上的語言是「不可處理」(Intractable)的,這是因為「指數函數」的增長速度遠
較其餘兩種函數高。以下讓我們比較指數時間與多項式時間的差別,設有兩個「全圖靈機」,輸入長度為n的字
符串後,它們分別須移動n2和2n步,並假設每移動一步需時0.0001秒。現設n = 100,
那麼前者的運算時間為0.0001秒 × 1002 = 1秒,而後者的運算時間卻是0.0001秒 ×
2100 = 4.02 × 1018年!
在「定理8」的層級中,PTIME與NPTIME的包含關係最引人注目,至今學者尚未搞清楚PTIME是否等於NPTIME。為
了探討這個問題,學者提出了「完備性」(Completeness)的概念。以下首先定義一些預備概念。設f為某種「形
式語言」上的函數,我們說f是「多項式時間可計算」(Polynomial Time Computable)的當且僅當存在一個可在
多項式時間內完成計算的「全圖靈機」Af,使得對任何輸入字符串w,Af都會停於「接
受狀態」,並且在計算結束時,「紙帶」上的字符串等於f(w)。
現在設有兩個「形式語言」L和L',我們說L'「多項式時間可歸約」(Polynomial Time Reducible)為L,記作L'
→PTIME L,當且僅當存在一個「多項式時間可計算」函數f,使得對任何字符串w,w ∈
L' ⇔ f(w) ∈ L。容易看到"→PTIME"具有傳遞性。
接著定義以下「形式語言」類別。設L為「形式語言」,我們說L是「非確定型多項式時間困難」
(Non-Deterministic Polynomial Time Hard)(記作NPTIME-H)的當且僅當對所有「形式語言」L' ∈
NPTIME,都有L' →PTIME L。從上述定義可以推出以下定理:
定理9:設L和L'代表兩個「形式語言」,若L' →PTIME L並且L ∈ PTIME,則
L' ∈ PTIME。
以下證明上述定理。根據PTIME和"→PTIME"的定義,我們有一個計算L的「確定型全圖靈機」
AL以及函數f,使得對任何字符串w,w ∈ L' ⇔ f(w) ∈ L,其中AL和f
都可在多項式時間內完成計算。現在我們設計一個計算L'的「確定型全圖靈機」AL'如下:給定任
何字符串w,首先計算f(w),然後用AL判定f(w),所得結果就是AL'計算w的結果。上述
AL'能在多項式時間內判定w,這是因為根據f的上述特性,我們有AL'接受w當且僅當
AL接受f(w),而且AL'作為AL和f的複合,也可在多項式時間內完成計算,
至此證得L' ∈ PTIME。
至此,我們可以定義以下「完備性類別」(Completeness Class)。設L為「形式語言」,我們說L是「非確
定型多項式時間完備」(Non-Deterministic Polynomial Time Complete)(記作NPTIME-C)的當且僅當L
∈ NPTIME ∩ NPTIME-H。根據上述定義,NPTIME-C是NPTIME的子集,而且其成員是NPTIME中最關鍵的
,這是因為若L ∈ NPTIME-C,那麼根據NPTIME-H的定義,對所有L' ∈ NPTIME,都有L'
→PTIME L。因此只要我們找到一個可在多項式時間內判定L的「確定型全圖靈機」
AL,那麼根據「定理9」的證明,我們便可以利用AL來設計可在多項式時間內計算L'的
「全圖靈機」。
接著提供NPTIME-C成員的實例,以下實例是一個「判定問題」(Decision Problem)。到目前為止,我們都把「
計算」定義為用某種「自動機」判定某種「形式語言」的過程。以下我們將採取一種較廣泛的定義,把「計算」
看成用某種「算法」(Algorithm)解決某種「判定問題」的過程,即在有窮步驟內判斷某種對象是否具備某種性
質的問題。請注意由於我們可以把上述「對象」和「算法」分別編碼為「形式語言」和「自動機」,所以上述
兩種定義是等價的。
NPTIME-C問題的一個實例是「圖論」(Graph Theory)中的「分團問題」(Clique Problem)。「分團問題」就是
:給定一個圖(Graph) G,G是否包含一個含有至少k個點的「完全子圖」(Complete Subgraph)的問題,其中k為
任意自然數,而「完全子圖」的意思則是指G的某個子圖,其中任意兩個點之間都有一條邊連接。舉例說,在以
下這個圖中,由點集{1, 2, 5}以及這三個點之間的邊組成的子圖便是含有至少3個點的「完全子圖」:

請注意在上述定義中,必須把k理解為變數。如果把k看成常數,則有關問題便屬於PTIME。
我們可以把計算命題的真值看成:給定一個語義模型M和命題p,判定p在M中是否為真的問題,由此我們亦可以 討論命題的複雜性。現在如果我們把某邏輯系統看成該系統所能表達的命題組成的集合,那麼我們有以下重要 定理(證明從略):
| 定理10: | (i) FO ⊂ LOGSPACE (ii) FO(+) ⊂ PTIME |
根據上述定理,日常語言中很多包含「一階可定義限定詞」的量化句都屬於LOGSPACE。至於包含其他常用量詞 的量化句,包括各種「整除性限定詞」(例如"(an even number of)")、「右比例限定詞」(例如 "most")和「右補右比例限定詞」等,由於這些量詞屬於FO(+)-D,因此都屬於PTIME。某些包含「結構 化量詞」的量化句,例如2.2.5小節介紹的"(an equal number of)"等,雖然不屬於FO(+),但也屬於 PTIME。因此,LOGSPACE和PTIME似乎涵蓋了幾乎全部「同構封閉單式量詞」,如要發掘不屬這兩個類別的命題 ,似乎只能從包含「多式量詞」的量化句或者某些特殊算子/結構的邏輯系統中尋找。以下筆者將從這兩方面 作一介紹。
筆者在《廣義量詞系列:量詞的迭代運算》和 《廣義量詞系列:非迭代多式量詞》中介紹了若干種構造「多式量詞」的運 算:「迭代」、「一元複合體」、「概括」、「分枝」、「累指」、「相互」等。Syzmanik在其博士論文 Quantifiers in TIME and SPACE: Computational Complexity of Generalized Quantifiers in Natural Language中討論了上述各種運算對量化句複雜性的影響,以下引述他的部分研究成果。為簡化討論,以下 集中討論由限定詞組成的量化句。我們有以下定理:
| 定理11: | 設Q、Q'為限定詞,並且以Q、Q'構成的量化句屬於 PTIME,則由Q、Q'經「迭代」、「一元複合體」、「概括」或「累指」運算所得多式量詞構成的量化句也屬於 PTIME。 |
以下證明上述定理,設AQ和AQ'分別為可在多項式時間內計算含Q和Q'量化句的算法。 首先考慮「迭代」運算,我們有以下定義:
其中
以下設計一種算法用來確定{x: Q'(B)(Rx)},對論域中每個x,重覆進行以下步驟:先確定(5)(請
注意在固定x後,(5)是一個一元謂詞,所以可以在多項式時間內確定),然後用AQ'判定量化句
Q'(B)(Rx)。如判定結果為真,則x ∈ {x: Q'(B)(Rx)}。用上述算法確定上述
集合後,我們便可以用AQ來判定量化句Q(A)({x: Q'(B)(Rx)})。以上整個過程都可在
多項式時間內完成。
其次考慮「一元複合體」,即對迭代量化句進行各種布爾運算的結果。這裡的「布爾運算」包括「外部否定」
、「內部否定」、「合取」和「析取」,以下逐一討論。對於「外部否定」,我們可以對Q(A)(B)的計算結果進
行簡單的變換(把「接受」變成「拒絕」,把「拒絕」變成「接受」),便可得到~Q(A)(B)的計算結果。對於「
內部否定」,由於Q~(A)(B) ≡ Q(A)(~B),我們可以先確定~B,然後再用AQ來判定Q(A)(~B)
,所得結果就是Q~(A)(B)的計算結果。對於「合取」,我們可以用AQ和AQ'分別判定
Q(A)(B)和Q'(C)(D),當且僅當兩個計算結果都是「接受」時,我們接受Q(A)(B) ∧ Q'(C)(D)。至於「析取
」,其算法跟「合取」大同小異,只須把前文的「接受」改為「拒絕」便可。容易看到,把上述四種運算作用
於屬PTIME的量化句,所得量化句也屬於PTIME。
其次考慮「概括」運算,我們有以下定義:
其中R、S為n元謂詞。由於Resn(QU)除了是以n元謂詞作為論元外,其真值條件與
QU具有完全相同的形式,因此含Resn(QU)與QU的量化句在計
算上的差異僅在於兩者語義模型的編碼方式,而編碼方式對計算複雜性沒有影響。
最後考慮「累指」運算,我們有以下定義:
請注意利用(4)和(5),可以把上式改寫為
由於上式是「迭代」和「合取」複合的結果,把「累指」運算作用於屬PTIME的量化句,所得量化句也屬於
PTIME。
在各種構造多式量詞的運算中,「分枝」和「相互」運算的情況較為複雜,這是因為把這兩種運算作用於不同
量詞,所得量化句的複雜性可能各有不同。以下重溫這兩種運算的定義(註7) :
當(9)和(10)中的量詞是固定的「左、右遞增絕對數量比較詞」時,所得量化句可表達為一階邏輯表達式,例如 當Q = (at least 2),Q' = (more than 1)時,(9)和(10)分別等同於以下兩式:
以上兩個量化句顯然屬於PTIME。請注意以上結果是在固定(9)和(10)中的Q、Q'的條件下才得到的,如果沒有這 個條件,即如果考察的對象是形如(9)和(10)的量化句,其中Q和Q'為限制在「左、右遞增絕對數量比較詞」中 取值的變項,那麼根據Syzmanik,這些量化句屬於NPTIME-C。事實上,當Q = (at least k)時,(10)的 判定問題相當於上一小節介紹的「分團問題」,而筆者在上一小節已指出,當我們把k看成變量時,「分團問題 」屬於NPTIME-C。
提高邏輯系統表達力的另一種方式是在邏輯系統中加入特殊的算子/結構,這是「描述複雜性理論」
(Descriptive Complexity Theory)的研究課題。「描述複雜性理論」是「計算理論」的一個分支,專門研究邏
輯系統的表達力與計算複雜性的關係。Fagin、Immermann、Vardi等人在這方面做了大量工作,本節主要引述
Immermann在Languages That Capture Complexity Classes一文中的部分研究成果。本小節討論的邏輯
系統都是「有序結構」,即論域中的所有元素均按某一順序排序。
一種較簡單的邏輯算子是「傳遞閉包」(Transitive Closure),記作TC。設R為某論域U上的二元關係,TC(R)就
是在U中包含R的最小傳遞關係。舉例說,設U為某個圖上的點集,對任何a, b ∈ U,R(a, b)代表有一條邊
連接a和b,那麼TC(R)便代表「圖論」上的「連通關係」(Connectivity)。具體地說,TC(R)(a, b)當且僅當有
一條「路徑」連接a和b,容易看到TC(R)滿足傳遞性。
以下是TC的形式定義,設R為U上的二元關係,a, b ∈ U,則
例如設U = {a, b, c, d, e},R = {(a, b), (b, c), (d, e), (e, d)},那麼我們有
請注意由於(11)包含對自然數變項n的存在量化,它是一階不可定義的,因此把TC加入「一階邏輯」中,可得到
比「一階邏輯」強的邏輯系統,稱為「傳遞閉包邏輯」(Transitive Closure Logic),記作FO(TC)。
另一種邏輯算子是「最小不動點」(Least Fixed Point),記作LFP。「不動點」本來是數學上的概念,給定函
數f,f的「不動點」就是滿足f(x) = x的數。如果有多於一個數滿足上述等式,我們便把最小的一個稱為「最
小不動點」。例如設f(x) = x2,f的「最小不動點」就是
我們可以把上述概念推廣應用於邏輯學。設F為把二元關係映射為二元關係的算子並且F滿足「單調性」,即若S ⊆ S',則F(S) ⊆ F(S'),則
以前述「傳遞閉包」的定義為例,(11)等價於
現在如果定義
我們便可以利用(12)-(14)把「傳遞閉包」TC(R)定義為LFP(F),這是因為LFP(F)是使F(S) = S為真的最小二元
關係S,而根據(13)和(14),我們正好有F(TC(R)) = TC(R),而且TC(R)是滿足這個等式的最小二元關係。從上
述討論可知,如果把LFP加入「一階邏輯」中,我們可得到比FO(TC)更強的邏輯系統,稱為「最小不動點邏
輯」(Least Fixed Point Logic),記作FO(LFP)。
此外,我們還有比上述兩者更強的「二階邏輯」(Second Order Logic)(記作SO)以及「二階邏輯」的
各種變體,包括「存在二階邏輯」(Existential Second Order Logic)(記作SO∃)(即只有「存
在量詞」的「二階邏輯」)、「二階(傳遞閉包)邏輯」(Second Order (Transitive Closure) Logic)
(記作SO(TC))和「二階(最小不動點)邏輯」(Second Order (Least Fixed Point) Logic)(記作
SO(LFP))。
學者研究了上述各種邏輯的複雜性,得出以下結果(證明從略)(請注意以下邏輯系統都是有序結構)(註8):
| 定理12: | (i) FO(TC) = NLOGSPACE (ii) FO(LFP) = PTIME (iii) SO∃ = NPTIME (iv) SO(TC) = PSPACE (v) SO(LFP) = EXPTIME |
本小節的內容雖然頗為抽象,但從廣義的觀點看,量詞表達的是集合的集合或集合之間的關係,而以上這些算
子/結構正可用來表達某些集合的集合或集合之間的關係,所以本小節的內容也可歸入廣義量詞理論的研究範
圍。此外,自然語言中某些結構,例如「統指量詞」(Collective Quantifier)和某些副詞,需要用「二階邏輯
」才能表達其語義,所以上述部分邏輯系統的理論在形式語義學上有其應用價值。
當代數理邏輯學還有其他增強表達力的方法,例如容許「無窮長命題」(Infinitary Proposition)的存在;加
入「計數器」(Counter)、「WHILE迴圈」(WHILE Loop)、「後繼函數」(Successor Function)、「額外謂詞」
(Extra Predicate)等,形成各種新穎的邏輯系統,本文無法一一介紹這些內容。


