筆者在《廣義量詞系列:時間量化結構》中介紹了「時間論域」上的量化結
構,一個自然的推論是,是否可以將「時間論域」推廣為「空間論域」(Spatial Domain),從而得到
「空間量化結構」(Spatial Quantified Structure)?但在事實上,語義學界對「空間」範疇的研究
遠少於對「時間」範疇的研究,這可能是由於「空間」的三維結構遠較「時間」的一維結構複雜。
不過,從另一角度看,人類經過千百年對幾何學、拓樸學、物理學的深入研究,已累積了對「空間」特性的豐
富知識。此外,對「空間」的感知也是人類的基本認知能力之一。事實上,在當今「認知語言學」的理論框架
中,無論是Lakoff有關「隱喻」(Metaphor)的理論,還是Langacker的「認知語法」(Cognitive Grammar),乃
至Talmy的「動力圖式」(Force Dynamics Schema),都與「空間」有著密切的關係。但遺憾的是,形式語義學
界對「空間」範疇的研究卻不多,其中一個較有影響的「空間」語義理論是由Zwarts、Winter等人開創的「向
量空間語義學」(Vector Space Semantics)。
有些人可能認為,在自然語言中,「時間」有豐富的「時」、「體」等「語法範疇」,容易引起人們注意。但
自然語言其實也有豐富的與「空間」有關的「語法範疇」,這就是「介詞」(Adposition)和「格
」(Case)。
傳統語法一向把"Preposition"列為基本詞類之一,"Preposition"一名在漢語中一般譯作「介詞」或「前置詞」
,這是因為在很多語言中,這類詞都放在它們所支配的名詞短語前("pre"這個「前綴」含有「前」的意思)。可
是通過「語言類型學」的深入研究,人們發現在某些語言中,扮演「介詞」角色的詞是放在它們所支配的名詞
短語後,這些詞應稱為"Postposition" (「後置詞」)。舉例說,英語的"through"除了作"Preposition"外,有
時也可作"Postposition",例如在"the whole night through"中,"through"便放在名詞短語"the whole
night"的後面。後來,人們還發現放在所支配名詞短語前後兩邊的"Circumposition",例如英語"from then
on"中的"from ... on",以及放在所支配名詞短語中間的"Interposition",例如以下拉丁語句子中的"cum":
| summa | cum | laude | |
| 最高 | 以 | 讚美 | = 「以最高讚美」 |
由於"Preposition"一名已不適宜用來概括上述具有相同功能但位置各有不同的詞,因此現代的「語言類型學」
為這類詞創造了"Adposition"這個新的名稱。不過,由於漢語的「介詞」一名本身並無位置的意思,筆者贊成
某些中國「語言類型學」者的主張,沿用「介詞」作為"Adposition"的譯名,並把"Preposition"、
"Postposition"、"Circumposition"和"Interposition"分別譯作「前置介詞」、「後置介詞」、「框式介詞」
和「中置介詞」。
Zwarts在Vectors Across Spatial Domains: From Place to Size, Orientation, Shape and Parts一
文中指出,「介詞」是自然語言中表達「空間」關係的最突出的詞類。當然,「空間」關係並非所有「介詞」
所能表達的唯一語義。但無庸置疑的是,對於最典型的「介詞」來說(例如英語的"in"、"on"以及漢語的「在」
、「到」等),「空間」關係的確是它們的最基本語義。有些學者更認為,上述「介詞」的很多其他語義其實都
是透過詞義引伸或「隱喻」從「空間」關係派生出來的。
除了「介詞」外,「格詞尾」(Case Ending)是表達「空間」關係的另一種重要語法形式(有關「格」的介紹,
請參閱拙文《論「格」(Case)》)。在某些含有多種「格」的語言(例如含
有15種「格」的芬蘭語以及含有17種「格」的匈牙利語)中,大部分「格」的作用便是表達「空間」關係。因此
我們可以說,這些語言中的「格」起著其他語言中「介詞」的作用。舉例說,匈牙利語便以"lakasban"表達英
語"in the house"的意思,其中"lakas"相當於英語的"house",而詞尾"ban"則起著相當於英語介詞"in"的作用
。由於這些「格詞尾」位於名詞詞根的後面,而它們在語義上又起著「介詞」的作用,因此我們可以把這些「
格詞尾」看成虛化(即失去單詞地位,變成黏著語素)的「後置介詞」(註1)。在這一種觀點下,「格詞尾」與「
後置介詞」便具有相同的性質。
看到這裡,有些讀者可能指出,在漢語中表達「空間」關係的詞類主要不是「介詞」,而是「方位詞」,即「
上」、「中」、「下」、「內」、「外」、「間」等,而當前漢語語法學界的主流意見則把「方位詞」看成「
名詞」的一個次類。不過,根據劉丹青的《語序類型學與介詞理論》一書,從「語言類型學」的角度看,漢語
的「方位詞」可以被視為「後置介詞」,而某些同時包含「前置介詞」和「後置介詞」的結構,例如「在...上
」等,更可被看成「框式介詞」。因此,在這種分析下,漢語跟其他語言相同,也是主要以「介詞」作為表達
「空間」關係的詞類。
此外,在自然語言中,還有一些無需借助「介詞」或「格詞尾」而能直接指稱地點的「處所名詞」,這些名詞
既可以是專有名詞(例如「香港」、"Britain"等),也可以是普通名詞(例如"site"、"area"等)。不過,由於從
句法功能方面看,「處所名詞」與一般表達個體的「可數名詞」(以下簡稱「個體名詞」)沒有甚麼分別,也能
充當主語、賓語等句法成分,所以我們不必把「處所名詞」與「個體名詞」區別看待,而可以把涉及「處所名
詞」的量化結構與涉及「個體名詞」的量化結構等量齊觀。舉例說,對於語句
我們可以把「處所名詞」"states"當作「個體名詞」處理,即定義一個由美國所有州份組成的集合STATE,並把 上句表達為以下「三分結構」(在下式中,c代表個體"the US presidential candidate"):
基於以上的討論,本文以下將集中討論以「介詞短語」形式出現的「空間量化結構」。
「向量空間語義學」的特點是利用數學上的「向量」概念來刻劃「介詞短語」所表達的「空間」關係。由於數
學和物理學的教科書已包含有關「向量」的豐富知識,本文不擬對「向量」作出詳細介紹,以下僅就本文所要
用到的概念作一些簡介。「向量」(Vector)是一種既有大小又有方向的量,在數學上通常用箭頭代表
「向量」,箭頭的長度代表「向量」的大小(又稱為「向量」的「模」Modulus或「範數」Norm),箭頭的指向則
代表「向量」的方向。基於「向量」的上述特性,它特別適合用來代表某些同時具有大小和方向的物理量,例
如「位移」、「速度」、「力」等。我們還可以對「向量」進行各種運算,包括「向量」的「加法」、「數乘」
(Scalar Multiplication)、「內積」(Inner Product)、求「逆」(Inverse)、求「模」等運算。
「向量」還有一種獨特的「分解」(Decomposition)運算,即把某「向量」分解為若干個「線性無關」
(Linearly Independent)的「分量」(Component)。在很多實際應用中,我們可以設定一個「笛卡爾坐標系」,
即選定一個「原點」、兩個或三個互相垂直的方向作為「坐標軸」,以及一個單位長度,這樣我們便可以定義
各個「坐標軸」方向上的「單位向量」(Unit Vector),並把任何「向量」表達為這些「單位向量」的「線性組
合」(Linear Combination)。

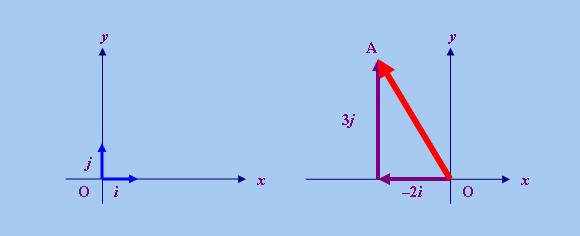
舉例說,在上面左圖中,我們選定了「原點」O、「坐標軸」x和y以及單位長度,這樣我們便有兩個「單位向量 」,分別為與x軸平行的i和與y軸平行的j (註2)。在上面右圖我們有一個「向量」OA (這種寫法表示該「向量」是以點O為「起點」Start-Point,並以點A為「終點」End-Point)。利用上述「單位 向量」,我們便可以把OA分解為兩個互相垂直的「分量」:−2i和3j,並且根據 「向量」的加法有:
請注意上式包含了「向量」之間的「加法」以及「實數」與「向量」的「數乘」(註3)。
有了以上的預備知識,我們便可以定義「向量空間」的概念。簡言之,「向量空間」(Vector Space)
是一種代數結構,這個結構包含由「向量」組成的集合V和「實數」組成的集合R (註4),以及V中元素之間的「
加法」運算(+)和R中元素與V中元素的「數乘」運算(•),並且這兩種運算滿足某些條件,例如對V中任意
兩個元素v和w,均有v + w = w + v等。此外,我們還可以定義
V中元素之間的「內積」(又稱「點積」Dot Product或「純量積」Scalar Product)運算,從而把「向量空間」
擴大為「內積空間」(Inner Product Space)。
「內積」的一個主要作用是表達「向量」在某一方向上的「分量」的長度。以上面右圖為例,「向量」
OA在x軸和y軸方向上的「分量」的長度分別為2和3。在向量代數上,我們可以用以下算式求得上述結果
:
上式表示當我們求某「向量」與某一方向上的「單位向量」的「內積」時,所得「內積」的絕對值就是該「向
量」在該方向上的「分量」的長度。根據「內積」的正負號,我們還可以判斷某「向量」的大致方向,這是因
為若「向量」v與某個軸上的「單位向量」的「內積」為正數,則代表v在該軸方向上的「分量」
與該軸同向;若為負數,則代表v在該軸方向上的「分量」與該軸反向;若為0,則代表v為「零
向量」(0)或者v與該軸垂直。仍以上面右圖為例,由於OA • i和
OA • j分別取負值和正值,這代表OA在x軸方向上的「分量」(即
−2i)與x軸反向,而在y軸方向上的「分量」(即3j)則與y軸同向。由此可以判斷
OA的終點位於第二象限。
此外,我們還可以透過「內積」定義「向量」的「模」。在數學上,通常把「向量」v的「模」記為
|v|,並且有
舉例說,利用上式,便可求得上面右圖中「向量」OA的「模」(從幾何學的角度看,「向量模」就是「 向量」的長度,因此以下結果亦可以用「畢氏定理」求得):
與「模」密切相關的另一個概念是點與點之間的「距離」(Distance)。在數學上,通常把點p與點q之間的「距 離」寫成Dist(p, q)。請注意如果p和q是以上述兩點為「終點」的「向量」,那麼我們可以利 用「模」來定義點與點之間的「距離」:
此外,我們還可以定義兩個點集合之間的「距離」。設A和B為兩個點集合,那麼A和B之間的「距離」就是A中元 素與B中元素之間的最小「距離」,即
在上面的定義中,min代表「最小值」(嚴格地說,這裡應使用「下確界」Infimum代替「最小值」,但為免引入
太多艱深的數學概念,這裡採用「最小值」作為「下確界」的近似概念)。
最後,我們還可以利用「內積」定義「向量」之間的「角度」。設有兩個「向量」v和w,那麼
它們之間的「角度」可用以下公式求得:
除了沿用數學上的「向量」和「向量空間」等概念外,「向量空間語義學」還引入一些新概念。Zwarts和
Winter在Vector Space Semantics: a Modeltheoretic Analysis of Locative Prepositions一文中定
義了「點域」和「向量域」的概念。「點域」(Point Domain) DP就是由某一範圍內所有
「點」組成的集合。由於「點」是幾何學上的基本元素,它自然成為「向量空間語義學」上的基本概念。
不過這裡存在一個問題,正如在「時間論域」下我們有時難以用「時刻」表達複雜的時間量,同樣在「空間論
域」下我們有時也難以用「點」表達複雜的空間量,因為有一些行為是不能在一個限定的細小空間範圍內完成
的。就以下句為例:
上句跟《廣義量詞系列:時間量化結構》中的某一個例句很相似,上句的問
題在於,我們難以說出愛恩斯坦是在美國內的哪一「點」發表「狹義相對論」,我們只能把上句看成籠統地說
愛恩斯坦在美國這一區域內完成了「發表『狡義相對論』」這個行為。因此,正如在「時間論域」下,我們需
要以「時段」作為基本元素;在「空間論域」下,我們需要以「區域」而非「點」作為基本元素。不過,由於
「空間」的結構較「時間」複雜,這裡所說的「區域」不像「時段」那樣具有固定的形狀,其形狀可以是不規
則的。在「時間論域」下,我們可以用「秒」、「分鐘」、「小時」等計量單位定義「時段」;但在「空間論
域」下,由於「區域」可以具有不規則的形狀,我們無法用標準的計量單位定義「區域」,因此這裡所說的「
區域」只能是籠統的概念,例如上句便是籠統地以整個「美國」作為「區域」。由此可見,上述「點域」中的
「點」實應改為「區域」才對。不過為免製造太多術語,本文將沿用「點域」此一名稱。
其實,以「區域」作為「空間論域」的基本元素實際上等於把「區域」當作「點」處理,這在科學研究和日常
生活中並非罕見的現象。舉例說,地球對我們來說雖然是龐然大物,但在計算地球圍繞太陽的軌道時,我們卻
可以把地球當作「點」處理,因為地球相對太陽來說只是一個「點」而已。同樣,在世界地圖上,像上海這樣
的大城市也只表現為一個「點」。由此可見,我們可以根據實際需要選取大小不等的「區域」作為「空間論域」
的基本元素,這一點就正如我們可以根據實際需要選取「秒」、「分鐘」、「小時」等「時段」作為「時間論
域」的基本元素一樣。
「向量域」(Vector Domain) DV則是由某一範圍內所有「向量」組成的集合。由於我們
可以利用兩個「點」定義一個「向量」(例如「向量」的「起點」和「終點」),所以「向量域」又可看成由「
點」的「有序對」組成的集合,即DV = DP × DP (註5)。
在本節我們將確定最簡單的「方位介詞」(Locative Adposition)的形式化定義。最簡單的「方位介
詞」稱為「非投射介詞」(Non-Projective Adposition),包括英語的"in(side)"、 "outside"、
"on"、 "at"、 "near"、 "between"、 "among"等。要確定含有這些介詞的句子的真假,我們只需知道物件之
間的相對位置。在作出定義前,我們需先作出一些假設。首先我們假設,本文所討論的「空間」都是「閉集」
(Closed Set)和「凸集」(Convex Set)。直觀地說,「閉集」是指包含其「邊界」(Boundary)以及邊界內所有
點的集合。至於「凸集」,則是指沒有任何凹陷位的形狀。有關「凸集」的精確定義,請參閱筆者的
《凸包(Convex Hull)》網頁。
接著設A為某個由「點」組成的集合,即「點域」DP的某個子集,而v是某個「向量」,即
「向量域」DV的元素。我們把A的「邊界」記作Boundary(A),把v的「起點」和「終點」分
別記作S-point(v)和E-point(v)。那麼我們有以下定義:若S-point(v) ∈
Boundary(A),則我們說v是A的一個「邊界向量」(Boundary Vector)。對應於Boundary(A)以
外每一點p,都有無限多個「邊界向量」以p為「終點」。在這無限多個「邊界向量」中,我們選擇長度最小的
一個「向量」v,稱為(對應於p的)「最近向量」(Closest Vector)。假如p ∈ A,我們
便說v是A的「內部最近向量」(Internally Closest Vector),記作Int(v, A);否則
便說v是A的「外部最近向量」(Externally Closest Vector),記作Ext(v, A)。現以
下圖說明上述概念:

在上圖中,橙色的長方形是點集合A,黑色的圍邊就是Boundary(A)。在圖中五個「向量」中,
v1-v3是「邊界向量」,v4和
v5則不是。對應於Boundary(A)以外的點p來說,v1是以p為「終點」的
長度最小的「邊界向量」。請注意對於其他「邊界向量」例如v2來說,均有
|v2| ≥ |v1|。由於p ~∈ A,所以v1是A
的「外部最近向量」,即Ext(v1, A)。同理,我們有Int(v3, A)。
有了上述概念,我們便可以確定「非投射介詞」"in(side)"和"outside"的定義(註6):
在上面,INSIDE和OUTSIDE被定義為「一元函項」,這兩個函項以點集合為輸入值,並輸出一個向量集合。舉例
說,假如我們的輸入值A就是上圖所示的那個橙色長方形,那麼INSIDE(A)就是所有像v3那
樣的「內部最近向量」組成的集合,而OUTSIDE(A)則是所有像v1那樣的「外部最近向量」
組成的集合。
INSIDE和OUTSIDE是最基本的「非投射介詞」,其他「非投射介詞」的定義都在上述定義的基礎上附加一些條件
,例如介詞"on / at"、"near"和"far away from"的定義便包含某種模糊成分:
在上述定義中,ON的輸出值是所有那些長度接近0的A的「外部最近向量」組成的集合。這裡之所以採用「接近0
」而非「等於0」,大概是為了遷就某些凹凸不平表面的情況。當我們把一個物體B放在一個凹凸不平的表面A上
時,B的某些點與A的最短距離可能大於0,所以使用上述定義能概括較多情況。至於NEAR和FAR-AWAY-FROM,其
輸出值則分別是所有那些長度少於某個標準s或大於某個標準s'的A的「外部最近向量」組成的集合。請注意這
裡的「接近0」、「少於某個標準s」和「大於某個標準s'」都涉及到語境和模糊語義的問題,這裡為簡化討論
,使用「≈ 0」、「< s」和「> s'」來表達這些概念,因此上述定義只是一種近似定義。
最後考慮"between"和"among"的定義,這兩個介詞的輸入值都包括超過一個點集合。為簡化討論,這裡只討論
"between",這個介詞的輸入值包括兩個點集合。這裡我們要用到「凸包」(Convex Hull)的概念。給定一個點
集A,該點集的「凸包」Hull(A)就是包含A中所有點的最小面積的凸多邊形(有關「凸包」的詳細介紹,請參閱
筆者的《凸包(Convex Hull)》網頁)。利用「凸包」的概念,我們可以作出如下定
義:
現以下圖說明上述定義:

在上圖中,由藍色粗線條框著的部分就是Hull(A ∪ B)。根據上述定義,BETWEEN(A, B)包括所有類似 v1-v3的「向量」,但不包括v4這樣的「向量」 (因為這個「向量」的「終點」不在Hull(A ∪ B)之內)。容易看到,上述集合內的「向量」的「終點」就是 直觀上位於A與B之間的點。
「方位介詞」還有另一個類別-「投射介詞」(Projective Adposition),這類介詞包括英語的 "above"、 "below"、 "under"、 "in front of"、"behind"、"beside"等(註7)。這類介詞跟「非投射介詞」 的區別在於,要判斷含有這些介詞的語句的真假,不能單靠物件之間的相對位置,還需要更多資訊,包括說話 者的所在位置、朝向以及物件的形狀、結構等。舉例說,在判斷語句
的真假時,我們不僅要知道樹與房子的相對位置,還要知道哪一方向是房子的「後面」。這個方向可能視乎說
話者所在的位置而定,也可能視乎房子門口的所在位置而定。由此可見,「投射介詞」的語義涉及頗為複雜的
問題。
為簡化討論,我們不考慮如何確定「上」、「前」、「右」這三個方向的問題。我們假設給定任何一個具體應
用問題,總能確定這三個方向,並分別用「單位向量」up、front、right表示,這三個
「單位向量」類似向量代數中的i、j、k,又稱為「軸」(Axis),以下用axis來
統稱這三個「軸」。以上述三個「軸」為基礎,我們還可定義更多概念。我們可以定義這三個「軸」的「逆」
−axis以代表「下」、「後」、「左」這三個方向,例如−up便是指向「下」的「
軸」。我們還可以定義與某個「軸」垂直的平面,例如對於up而言,⊥up便代表與
up垂直的平面,即水平面(假如我們只考慮二維空間,那麼⊥up則代表與up垂直的
直線,即水平線)。
根據向量代數,給定任一「向量」v,我們可以把v分解為兩個「分量」之和,其中一個「分量」
與某個axis平行,我們把這個「分量」記作vaxis;另一個「分量」則與
axis垂直,即在平面⊥axis上,我們把這個「分量」記作v⊥axis
。換句話說,給定任一「向量」v,我們有
請注意根據向量代數,我們有
利用上述概念,我們便可以定義介詞"above"、"below / under"、"on / to the right of"、"on / to the left of"的語義:
上面之所以採取如此複雜的定義,是為了遷就下圖的情況:

在上圖中,p和q是A以外的點,v是以p為「終點」的「向量」。該「向量」被分解為
vup + v⊥up,其中vup與up平行,
v⊥up則在直線⊥up上。由於v • up > 0,這說明
v在垂直方向上的「分量」(即vup)與up同向,即v大致上是向上指
的。此外,由於|vup| > |v⊥up|,「向量」v符合上述
ABOVE(A)的另一條件,所以我們可以說點p位於A的上方。
上述例子顯示"above"等介詞語義的廣泛性,儘管點p並非位於A的正上方,但由於v與
vup的夾角少於45°,我們仍可認為該點是位於A的右上角的上方。事實上,在上圖中兩
條綠色虛線夾著的範圍內(不包括綠色虛線)的點都可認為是位於A的右上角的上方。容易驗證,所有以A的右上
角為「起點」並以上述範圍內的點為「終點」的向量v都滿足|vup| >
|v⊥up|。至於上圖中的點q,由於不在上述範圍內,所以我們認為該點不在A的右上角
的上方,因而也不在A的上方。
最後討論介詞"beside"的語義,我們可以把這個介詞看成相當於"on the right or left of",這樣便可以把這
個介詞定義為
容易看到,上式其實是ON-THE-RIGHT-OF(A)與ON-THE-LEFT-OF(A)的結合。
除了表示靜態位置的「方位介詞」外,我們還有表示動態位置的「方向介詞」(Directional
Adposition)。自然語言中的「方向介詞」一般可以根據其所表示動態的部分而分為三類:(1)源點介詞(Source
Adposition),例如英語的"from"、"out of"、"away from"等;(2)終點介詞(Goal Adposition),例如英語的
"onto"、 "into"、 "towards"、 "up"、 "down"等;(3)路線介詞(Route Adposition),例如英語的"across"
、"through"、 "(a)round"、 "over"、 "along"等。
由於「方向介詞」表達某一物件的位置相對於某一點集A的變化,我們可以把這種位置變化看成以Boundary(A)
上的點為「起點」的「向量」構成的「路徑」(Path),用數學語言表達就是把區間[0, 1]映射到以
Boundary(A)上的點為「起點」的「向量」的函項。我們把這個函項記作θ,這樣
θ(0)便代表「路徑」的源點向量,θ(1)則代表「路徑」的終點向量。為了保證所
得「路徑」是連續的,我們還規定θ是連續函項。此外,為了與前文介紹的「最近向量」相協調
,我們還規定本文所指的「路徑」是A的「最近路徑」(Closest Path),即對所有t ∈ [0, 1]而
言,θ(t)都是A的「最近向量」。我們用Closest(θ, A)表示θ是A的
「最近路徑」。現以下圖說明上述概念:

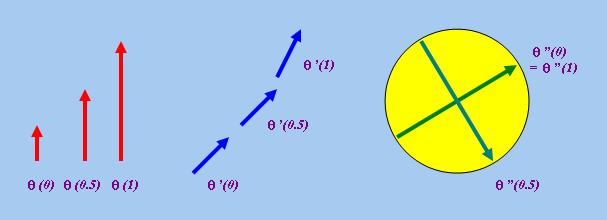
上圖刻劃"over A"的語義,θ (即藍色虛線)代表符合"over A"語義的其中一條「路徑」。
θ的輸出值都是A的「最近向量」,其中θ(0)、θ(0.5)和
θ(1)分別為該「路徑」的源點向量、中間點向量和終點向量。請注意"over A"的語義並不要求整
條「路徑」都必須在A的上方,例如在上圖中θ' (即綠色虛線)便是另一條符合"over A"語義的「
路徑」。
根據以上討論,我們可以把「方向介詞」看成由「路徑」組成的集合,而且很多「方向介詞」都與某些「方位
介詞」在語義上有關連。舉例說,前述的"over"便在語義上與「方位介詞」"above"有關連。不同類別的「方向
介詞」與「方位介詞」的關連方式各有不同:「源點介詞」在「路徑」的源點上與「方位介詞」有關連,「終
點介詞」在「路徑」的終點上與「方位介詞」有關連,而「路線介詞」則在「路徑」的某一段上與「方位介詞」
有關連。以下首先給出「源點介詞」和「終點介詞」的形式化定義:
以上定義顯示,每個「方向介詞」的輸出值都是由A的「最近路徑」組成的集合,每個「方向介詞」在源點或
終點方面與某個「方位介詞」有關連,例如FROM(A)的定義便規定,有關「路徑」的源點必須在A之上,這反映
了"from"的語義(註9)。
接著考慮「路線介詞」的定義。由於這類介詞的語義涉及有關「路徑」的某一段,所以它們的定義較為複雜,
現列出如下:
在自然語言中,某些「方位介詞」在與表達動態的動詞連用時,也會獲得「方向介詞」的語義,試看下句:
在上句中,「方位介詞」"under"在與動詞"swam"連用後獲得了「路線介詞」的語義。仿照上文,我們可以把上 句中的"under"定義為:
上式中的UNDERd帶有下標d,表示它是一個「方向介詞」,以區別於一般的「方位介詞」UNDER。其
他「方位介詞」變成「方向介詞」的情況類此,這裡不再贅述。
並非所有「方向介詞」都可借助某個「方位介詞」來作出定義,對於這些「方向介詞」,我們要用其他方法作
出定義。舉例說,由於"towards A"和"away from A"分別含有「逐漸接近A」和「逐漸遠離A」的意思,我們可
以用有關「路徑」上的「向量」與A的「距離」的變化來定義這兩個「方向介詞」(註10):
接著討論"up A"和"down A",這兩個介詞短語所表達的語義有以下特點:它們表達的「路徑」必須一直保持在 物體A上,並且其終點的水平高度須高於或低於其源點的水平高度。為此,我們引入符號Level(p)代表點p的「 水平高度」。根據以上規定,我們便可以把"up A"和"down A"定義為
最後討論介詞"(a)round"的定義,這是一個多義詞,"(a)round A"既可表示「在A以外圍繞A(至少)一周」的意 思(例句:The earth moves around the sun.),也可表示「在A以內走遍A的邊界或大部分地區」(例句:John walked around the park.),本文只討論第一種意思。對於這種意思,我們可以利用有關「路徑」上各「向量」 與源點向量的夾角來作出定義,即上述夾角應窮盡區間[0°, 360°)內的所有實數。這樣,我們便有以 下定義:
請注意上式沒有規定有關「路徑」的具體形狀,但卻規定了「路徑」上各「向量」必須為A的「外部最近向量」
,並且各「向量」(即θ(t))與源點向量(即θ(0))的夾角須窮盡區間[0°,
360°)內的所有實數,這反映了"(a)round A"的上述第一種意思。
在自然語言中,我們有時可以用「方向介詞」表達「方位介詞」的意義。舉例說,在語句
中,「方向介詞短語」"along the railway"所表達的不是動態的「路徑」,而是靜態的位置。為了準確表達 這個介詞短語的意思,我們要把它所代表的「路徑」集合轉化為「向量」集合。這樣,我們便得到以下定義:
上式中的ALONGl帶有下標l,表示它是一個「方位介詞」,以區別於一般的「方向介詞」ALONG。 其他「方向介詞」變成「方位介詞」的情況類此,這裡不再贅述。
到目前為止,我們討論的還只是介詞短語而不是整句的形式化表達法。在本小節我們將討論一種簡單句子的表 達法,這種句子以"be"作謂語動詞並以介詞短語作為主語補語,表達靜態的空間關係。首先考慮以下語句:
由於上句的意思是John整個人都在房子內,我們可以把上句表達為集合之間的包含關係。可是這裡存在一個問
題,在「向量空間語義學」的框架下,介詞"inside"被處理成把點集合(即DP的子集)映射為向量集
合(即DV的子集)的函項INSIDE。可是上句中的"John"和"the house" (以下分別用j和h代表)作為「
專有名詞」和「有定摹狀詞」,卻是「個體論域」U中的元素,不適合作為INSIDE的輸入值或輸出值。為此,我
們必須對這些名詞短語進行「類型轉換」(Type Shifting)。
我們可以引入一個轉換函項Loc,它的作用是把「個體論域」U中的元素映射為該元素所在位置的點組成的集合
,例如Loc(j)和Loc(h)便分別代表John和房子所在位置的點組成的集合。透過這個函項,我們便可以把INSIDE
作用於Loc(h),所得結果INSIDE(Loc(h))為從房子的邊界向內指的「向量」組成的集合,即代表「房子內」的
「向量」集合。由於Loc(j)和INSIDE(Loc(h))分別為點集合和向量集合,我們必須借助函項E-point把「向量」
轉化為「點」後才能進行集合運算。因此我們最終把語句(1)表達為以下含有集合包含關係「⊆」的「量化
結構」:
在上式中,變項p和v分別為DP和DV的元素,這裡為簡化表達式,所以略去「
∈ DP」和「∈ DV」這兩個條件,下文亦作相同處理。上式的意思是,John
所在位置的每一點都是代表「房子內」的某個「向量」的「終點」。換句話說,John整個人位於房子之內,這
正是上句的意思。
在上面我們把含有介詞"inside"的語句處理成集合之間的包含關係,此一方法也適用於包含其他介詞的語句。
試看以下語句:
儘管語句(1)和(3)表達兩種截然相反的空間關係,但由於我們把所有「方位介詞短語」都處理成向量集合,這 兩句都可表達為John所在位置的每一點都是某個「向量集合」內的「向量」的「終點」。這樣上句便可表達為
請注意上式跟(2)非常相似,兩式的差異僅在於(2)使用函項INSIDE,而上式則使用OUTSIDE。由於INSIDE和 OUTSIDE是最基本的「方位介詞」,其他「方位介詞」的定義都建基於這兩個介詞,我們可以得出結論:包含「 方位介詞短語」的靜態句都應表達為集合之間的包含關係。
除了上一小節討論的靜態句外,介詞短語亦可出現於含有其他動詞的語句中,例如以下語句:
由於上句包含"John is standing"此一信息,我們不能單純採用Loc(j)來表達John站立位置的點集,但可以引 入一個函項Place(s),這個函項的論元是代表命題的變項s,其輸出值就是在「點域」DP中使命題s 為真的點的集合。利用此一函項,我們可以把上句表達為
類似地,對於包含「方向介詞短語」的句子,我們引入另一個函項Route(s)。這個函項的論元也是命題變項s, 其輸出值則是使命題s為真的「路徑」組成的集合。試看以下語句:
類似對語句(5)的處理方法,我們把上句表達為含有集合包含關係「⊆」的量化結構:
除了作為句子中的狀語外,介詞短語亦可作為定語(即名詞修飾語)。作定語的介詞短語可以像 《廣義量詞系列:特殊單式量詞》介紹的「相交形容詞」那樣處理成集合, 並與代表名詞中心語的集合構成「交集」。不過,由於介詞短語是「向量」集合或「路徑」集合,我們必須先 把這些集合轉換為「個體」集合,才能進行上述「交集」運算。我們可以使用前述函項Loc的「逆函項」 Loc−1,這個函項把某個點集合轉化為這些點所在之處的個體的集合。利用這個函項,我們 便可以把名詞短語
表達為
在上式中,{p: ∃v: ∈ INSIDE(Loc(h)) (p = E-point(v))}是代表「
房子內」的「向量」的「終點」組成的集合。把Loc−1作用於這個集合後,便得到這些點所
在之處的個體的集合,即「房子內的東西」的集合。把這個集合跟CHAIR相交後,便得到「房子內的椅子」的
集合。
運用上述原理,我們還可以表達某些多重介詞短語。舉例說,在以下「雙重介詞短語」中,
介詞"on"的賓語是名詞短語"the chair inside the house",而後者又是由介詞短語作定語的名詞短語。利用 前述(7)的集合論表達式(8),我們可以把上述「雙重介詞短語」表達為
以上兩小節討論的內容適用於表達物體的空間位置或運動路徑的語句,但對於表達物體間距離的語句卻並不適 合。試看以下語句:
以上語句可用下圖表示:

上圖中的虛線圓形代表NEAR(Loc(h))的範圍,其中s代表某長度標準。從上圖可以看到,要令上句真,只需 Loc(j)的部分點(即離Loc(h)最近的那些點,例如p)在NEAR(Loc(h))的範圍內便可以。事實上,即使Loc(j)上的 點q離Loc(h)較遠,也無損於上句的真實性。因此,對於表達距離的語句而言,不適宜像上面(2)那樣表達為 Loc(j) ⊆ {...}的形式,因為這裡無需要求整個Loc(j)被包含在集合{...}內。為正確表達上句的語義, 我們需要把Loc(j)換成另一個點集合,即Loc(j)中離Loc(h)最近的那些點組成的集合,這個集合就是{p ∈ Loc(j): Dist({p}, Loc(h)) = Dist(Loc(j), Loc(h))}。利用這個集合,我們可以把上句表達為
除了NEAR外,前面介紹過的ON和FAR-AWAY-FROM的語義也涉及距離概念,所以也要作類似的處理。此外,自然語 言還有一種表達距離的方法,就是在介詞短語前加某些修飾語。對於這些修飾語,我們可以把它們處理成「向 量」集合,並與代表介詞短語的「向量」集合構成「交集」。我們把這類修飾語稱為「相交修飾語」 ,包括表達絕對距離(例如"10 m")、相對距離(例如"halfway")和模糊距離(例如"just"、"far")的修飾語。下 表列出部分「相交修飾語」的集合論表達法:
| 相交修飾語 | 集合論表達法 |
|---|---|
利用上表,我們可以表達某些含「相交修飾語」的介詞短語。舉例說,介詞短語
便可以表達為
這樣,語句
便可以表達為
上表並未列出「相交修飾語」"halfway"的集合論表達法,這是因為這個詞的語義不僅涉及「向量」變項 v的長度,也涉及介詞賓語的某個度量。試看以下語句:
上句可以被理解為,John所在的位置剛好是樹與房子之間的中間位置。為了表達此一意思,我們要用到樹(用t 代表)與房子(用h代表)之間「距離」的概念。由於函項Dist是以點集合為論元,我們首先要用函項Loc把個體t 和h轉化為點集合,這樣樹與房子之間的距離就是Dist(Loc(t), Loc(h)),而上句便可表達為
當"halfway"與其他介詞短語連用時,我們便要定義其他度量,例如對於"halfway inside the tunnel",我們
便要定義隧道的長度,這裡不再深入討論。
除了表達距離外,我們還有表達方向的「相交修飾語」"straight",當這個詞與不同介詞短語連用時,所涉及
的方向可能各有不同。試看以下語句:
上句的意思是燈懸吊在盒子的正上方,用向量代數的語言說,就是從盒子指向燈的「向量」v與 up平行,即v的「分量」v⊥up等於0。根據以上討論,我們可 以把上句表達為下式(以下用b和l分別代表"the box"和"the lamp"):
請注意這裡要運用前面第3節討論到的「區域」概念才能正確理解上式。由於燈與盒子各有不同的形狀,由盒子
的某一點指向燈的某一點的「向量」不可能全部都是垂直的,這豈不意味著上式是假的?不過,我們可以「區
域」而非「點」作為「空間論域」的元素,把燈和盒子看成兩個「區域」,並以這兩個物件的幾何中心代表這
兩個「區域」(這在實質上等同於把燈和盒子當作「點」處理),那麼當燈的幾何中心剛好位於盒子的幾何中心
的正上方時,上式便是真的,而這也正好符合上句的直觀意義。
當"straight"與「方向介詞短語」連用時,它所代表的意思是,該介詞短語所代表的「路徑」是筆直的,從向
量代數的角度看,這就是「路徑」上各個「向量」都與「源點向量」平行(亦即兩者的夾角等於0)。因此語句
便可以表達為下式(以下用c代表"the corridor"):
在前面各小節,句子的主語與介詞短語的關係都被處理成集合的包含關係。不過,假如我們在介詞短語前加上 某些特殊的修飾語(例如"partly"、"everywhere"等),便可能改變這種關係,筆者把這類修飾語稱為「量 化修飾語」。修飾語"partly"在語義上的作用是告訴我們語句的行為只是部分地在介詞短語表示的範圍內 進行。舉例說,語句
便應表達為下式(以下用c和g代表"the car"和"the garage"):
上式的意思是說,汽車有一部分位於車房內,一部分位於車房外,這表達了"partly"的意思。當然我們還可以 用「相對數量比較詞」標出汽車有多大一部分位於車房內,例如下句中的"more than half":
相應地,我們也要用對應於量詞"(more than 1/2)"的形式表達上句的意思:
修飾語"everywhere"、"somewhere"、"nowhere"等則是對介詞短語所表達的空間範圍的限制。其實我們可以認 為,含有一般介詞短語的語句都隱含著修飾語"somewhere"。舉例說,語句(6)便可以理解為等同於
當然如果我們想強調"somewhere"與量詞"some"的對應關係,我們可以把上句表達為
請注意上式可以從式(6)推導出來。
當句子的「量化修飾語」是"everywhere"或"nowhere"時,我們便要使用對應於量詞"every"或
"no"的表達式。舉例說,語句
便可以分別表達為
請注意語句(9)的表達式(10)中的「點」應理解為「區域」,因為當我們說出(9)時,我們的意思不大可能是說
John逛遍了房子內的每一個空間點,而只是籠統地說John逛遍了房子內的每一個部分。
"everywhere"、"somewhere"、"nowhere"等副詞其實不一定要作為介詞短語的修飾語出現,它們也可以單獨出
現以表達空間位置,這時有關的表達式便無需帶有介詞的信息。舉例說,語句
便可以表達為
由於「點域」DP具有「全集」的性質,上式在邏輯上等同於
上式的意思是說,John閑逛的範圍等同於整個「點域」,這正好反映了"everywhere"所要表達的意思。
最後還要談談"there"和"where",這兩個副詞一般都單獨出現,它們分別對應著「個體論域」上的「指示詞」
和「疑問量詞」,因此我們可以沿用以往介紹有關「指示詞」和「疑問量詞」的處理方法表達含有這兩個副詞
的句子的語義。舉例說,語句
便可以分別表達為
請注意在上面第一式中,筆者把「指示詞」"there"處理成「語境函項」there(X'),該函項以語境X'為輸入值 ,並以一個點集合為輸出值。
空間是人類認知中的一個極為重要的範疇。除了上述的「方位介詞」和「方向介詞」外,自然語言中還有多種 表達空間關係的方法,所能表達的空間關係也不只「方位」和「方向」兩種。以下將主要根據Zwarts的 Vectors Across Spatial Domains: From Place to Size, Orientation, Shape and Parts一文簡介「 空間論域」上的其他量化現象。
Zwarts在其文章中區分了「位置向量」(Place Vector)和「軸心向量」(Axis Vector)這兩 個概念。「位置向量」用來表達物體之間的相對位置,此即前文一直使用的「向量」概念。「軸心向量」則代 表某物體的「軸心」,它是物體的組成部分之一。下圖顯示這兩種「向量」的區別:

上面左圖顯示一個從點p指向點q的「位置向量」v,右圖的A則是一個長方形物體(亦可看成圓柱體的某
個切面),圖中的v就是該物體的「軸心向量」。我們可以仿照Zwarts,使用Axis(A, v)的形式
表示向量v是物件A的「軸心向量」。
「位置向量」與「軸心向量」是兩個既有區別又有關聯的概念,因此我們可以利用它們的關聯來表達某些空間
關係。首先,「大小」(Size)的概念與空間位置的概念便存在對應關係。舉例說,語句
便可以改寫為
基於"short"與"near"的這種對應關係,我們可以利用前面有關介詞"near"的定義把語句(11)表達為下式(以下 用u代表"the umbrella",s則代表某種長度標準):
其次,物體的「方向」(Orientation)可以理解成「軸心向量」的方向。舉例說,根據"upside down"與方向 up的關聯,我們可以把語句
表達為
最後,某些表達物體「部分」(Part)的概念也與空間位置存在對應關係。舉例說,英語中很多表達空間位置的 介詞,例如"in front of"、"at the back of"、"to the side of"、"on top of"等便是來自物體「部分」的 名稱。利用這種對應關係,我們可以表達某些涉及物體「部分」的語句。舉例說,語句
便可以表達為下式(以下用c代表"the car",並假設汽車的「軸心」是從車尾指向車頭):
在上式中,{p: p = E-point(tv) ∧ 0.5 < t < 1}代表所有那些其長度超過汽車一半長度的「向量 」終點組成的集合,因此這個集合就是汽車「前部」的點組成的集合。請注意上式實際上只考慮汽車「軸心」 (即一維空間)上的位置,而沒有考慮John和汽車的不規則形狀。
為了表達某些動態空間關係,Zwarts區分了「位置路徑」(Place Path)與「軸心路徑」
(Axis Path)的概念。前者就是前面第6節介紹的「路徑」,它表達物體之間的相對位置的變化;後者則代表某
物體軸心的路徑,它表達該物體本身的變化趨向。仿照上一小節,我們可以用Axis-Path(A, θ)
來表示θ是物體A的軸心的「路徑」。
利用「位置路徑」與「軸心路徑」的對應關係,我們可以表達某些物體的運動變化。以下筆者將介紹三種運動
變化,下圖顯示以下三個例句中的「軸心路徑」:
首先,我們可以表達物體「大小」的變化。試考慮以下語句:
上句可以用John的「軸心路徑」θ來表達(見上面左圖),在θ上的所有「向量」都 是垂直向上的,並且這些「向量」的長度在不斷遞增。根據以上分析,我們可以把上句表達為:
其次,「軸心路徑」的概念可以用來表達物體位置或方向的變化。試考慮以下語句:
如果我們以鳥的身體作為其「軸心」,那麼上句所描述的是一個逐漸上升的「軸心」的「路徑」 θ'(見上面中圖),而且這個「軸心」的方向是大致朝上的(儘管不一定垂直向上)。綜合以上討論 ,我們可以把上句表達為下式(以下用b代表"the bird",並用Level(p)代表點p的水平高度):
最後,我們還可以用「軸心路徑」的概念來表達某些物體的「形狀」(Shape),這是因為某些「形狀」可以被表 述為運動「軌蹟」(Locus)。以下筆者將使用Locus(θ)表示「軸心路徑」θ的「軌 蹟」(即該「軸心」在「路徑」上所曾經過的空間點的集合)。利用這個概念,我們便可以把語句
表達為下式(以下用d代表"the disk"):
上式是說,碟子所在位置的點集Loc(d)等於碟子的「軸心」(即碟子的某條「直徑」)所走過的「路徑」 θ''(見上面右圖)留下的的「軌蹟」(即上面右圖中黃色的部分),而這個「路徑」是一個「旋轉」 運動。在這個運動中,「路徑」上各「向量」的長度保持不變,而且「路徑」上各「向量」與源點向量的夾角 窮盡區間[0°, 180°)內的所有實數(註12)。
在7.1小節筆者把介詞處理成「一元函項」,並把大多數包含介詞的語句處理成集合之間的包含關係,這相當於
把這類句子處理成「全稱量化句」,這種處理方法著眼於主語與介詞短語之間的關係。現在如果我們把介詞看
成兩個名詞短語(即主語與介詞賓語)之間的中介,我們將看到某些介詞與量詞存在微妙的對應關係。除了介詞
外,某些表達空間關係的動詞/形容詞,例如表達「重疊」關係的動詞/形容詞"overlapping",也與量詞存在
對應關係。
當我們使用集合論語言表述量詞的語義時,這種對應關係便特別明顯,這是因為在數學上,我們常可用「溫氏
圖」表達集合之間的關係,而圖形之間的關係正是一種空間關係。舉例說,"inside"、"outside"和
"overlapping"便分別與量詞"every"、"no"和"some"相對應。用幾何語言表達,我們可
以把
分別表達為以下「三分結構式」(為簡化討論,以下把介詞理解成表達點集合之間的關係,而略去向量的概念) (註13):
這樣我們便把"inside"、"outside"和"overlapping"解釋成「點域」 DP上的量詞。我們甚至可以 把上述詞項處理成類似「<1,1>型量詞」的「二元函項」,而把上述「三分結構式」改寫為更簡潔的形式:
其他表達空間關係的詞項也可作類似的處理。以下筆者將把這些詞項處理成「二元函項」,並以斜體
表示。
上述對應關係還表現在「對稱性」和「傳遞性」方面。首先討論「對稱性」,我們知道在上述三個量詞中,只
有"no"和"some"是對稱的,例如
有趣的是,介詞"outside"和"overlapping"也是對稱的,例如
其次討論「傳遞性」,在上述三個量詞中,只有"every"是傳遞的,例如
與此對應,介詞"inside"也是傳遞的,例如
至於其他介詞,則情況較為複雜。儘管根據前面的討論,絕大多數「方位介詞」的語義都包含著 "outside"的語義,但不能就此推斷,這些「方位介詞」都與量詞"no"存在對應關係。事實上, 在本文討論過的「方位介詞」中,只有"near"、"(far away from)"、"beside"以及帶 有「相交修飾語」的"(10 m away from)"等具有對稱性。試比較
而"above"、"(below / under)"、"(on / to the right of)"、"(on / to the left of)"等卻具有傳遞性,例如
這樣看來,上述這些介詞反倒與量詞"every"有相似的性質。不過,筆者在這裡必須強調,除了 "inside" 、 "outside"和"overlapping"這三個詞外,其他「方位介詞」與量詞的對應 關係都是不完全的,這是因為這些「方位介詞」的語義除包含點集之間的關係外,還包含方向、距離等信息, 因此不能把這些「方位介詞」簡單比附為「點域」上的量詞。
在前面的討論中,所有介詞短語都是以「專有名詞」或「有定摹狀詞」作為介詞賓語,如果我們不考慮「專有
名詞」或「有定摹狀詞」的內部結構,這兩種詞類都可簡單地表達為個體常項。但除此以外,在自然語言中介
詞短語還可以「量化名詞組」(即帶有量詞的名詞短語)作為介詞賓語,本小節討論這類介詞短語的形式化表達
法。
如果介詞短語含有「量化名詞組」,有關量詞的轄域一般都大於介詞的轄域。試考慮語句
由於John和Mary不可能於同一時間在兩個不同的地點碰頭,上句其實是表達至少兩個「John碰見Mary」的事件 ,而這些事件的發生地點包含至少兩個圖書館。根據此一分析,上句的準確意思應為
把上句改寫為上述形式,我們便可把該句表達為以下「三分結構」:
請注意在上式中,我們把表示「事件」的變項e定為Power(T)的元素,這裡T代表「時間論域」,Power(T)則代
表「時間論域」的「冪集」,這是因為筆者在《廣義量詞系列:時間量化結構》
中把「事件」定義為由「時段」(即T的元素)組成的集合,因此e是T的子集,亦即Power(T)的元素。此外,
在上式中筆者用inside(PLACE(e))(Loc(x))表示「John碰見Mary」的事件發生在x之內。由於x是「個體
論域」中的元素,我們必須先用函項Loc作用於x,以得到一個「點集合」Loc(x),然後才可以Loc(x)作為
"inside"的論元。此外,我們也假設上式中的PLACE是把「事件」映射為「點集合」的函項,所以
PLACE(e)可直接作為"inside"的論元。
為貫徹「三分結構」的表達法,我們還可以把上式改寫為


