Studie porovnává tři algoritmy nalezení K-tého nejmenšího z N prvků: Hoarův FIND [1], moji modifikaci programu FIND [3] (nazval jsem jej MODIFIND v Algorithms, Data Structures, and Problems Terms and Definitions of the CRC Dictionary of Computer Science, Engineering and Technology, version February 4, 1999) a Floydův a Rivestův SELECT [4], [5]. Pro měření doby výpočtu, počtu porovnání a výměn prvků jsem využil implementace algoritmů v jazyce Rexx (Quercus Systems' Personal REXX for Windows) na počítači PC s procesorem 6x86MX-PR233, 32MB RAM v prostředí Windows 98.      Problém nalezení K-tého nejmenšího z N prvků definoval C. A. R. Hoare v [1] takto: Je dáno pole A obsahující N navzájem různých prvků a celé čílo K, 1 <= K <= N, má se určit K-tý nejmenší prvek A a pole se má přerovnat tak, aby prvek A[K] výsledného pole byl K-tým nejmenším prvkem a všechny prvky s indexem menším než K měly menší hodnotu a všechny prvky s indexem větším než K měly větší hodnotu. Musí tedy platit: A[1], A[2], ..., A[K - 1] <= A[K] <= A[K + 1], ..., A[N] Řešení tohoto problému můžeme využít v praxi pro nalezení mediánu nebo jiného kvantilu stejně jako pro určení nejmenšího, největšího nebo druhého největšího atd. prvku. Přímočaré řešení - pole nejdříve vytřídit - by mohlo být časově náročné při velkém počtu prvků. Rychlejší algoritmus publikoval poprvé C. A. R. Hoare a nazval jej FIND. V této práci jej budu označovat jako H. Algoritmus H      Hoarův algoritmus je založen na zřejmém důsledku známé definice: DEFINICE K-tý nejmenší z N prvků je ten prvek pole, který je menší než K - 1 jiných prvků ale větší než N - K prvků. DŮSLEDEK Prvek nemůže být K-tým nejmenším prvkem pole, je-li větší než K (a více) jiných prvků nebo menší než N - K + 1 (a více) jiných prvků.     Při výpočtu vyjdeme z předpokladu, že A[K] je K-tým nejmenším prvkem a pokusíme se to dokázat následujícím postupem: Pole se prohlíží zleva (tj. zkoumají se prvky s indexy I = 1, 2, ...) až se nalezne prvek A[I] >= A[K], pak se prohlíží pole zprava (tj. zkoumají se prvky s indexy J = N, N - 1, ... ) až se nalezne prvek A[J] <= A[K], oba prvky se vymění, v procesu zkoumání a výměn se pokračuje tak dlouho, dokud se ukazatelé I a J nestřetnou. Pak může nastat jeden ze tří možných případů: PŘÍPAD 1 (J < K < I) Tvrzení je dokázáno. K-tý nejmenší prvek je na správném místě a program končí. Příklad: PŘÍPAD 2 (J < I <= K) Prvky A[1] ... A[J] jsou menší než N - K + 1 jiných prvků, přesně řečeno jsou menší než N - I + 1 >= N - K + 1 prvků, žádný z nich tedy nemůže být K-tým nejmenším prvkem. Pokračovat ve výpočtu proto budeme hledáním prvku, který je (K - I + 1)-ním nejmenším prvkem v poli A[I] ... A[N]. Příklad: PŘÍPAD 3 (K <= J < I) Prvky A[I] ... A[N] jsou větší než K jiných prvků, přesně řečeno jsou větší než J >= K prvků. Žádný z nich tedy nemůže být K-tým nejmenším prvkem. Pokračovat budeme v řešení úlohy redukovaného rozsahu: Nalézt K-tý nejmenší prvek pole A[1] ... A[J]. Příklad:     Popsaný algoritmus ilustruje program H, který je mým překladem programu Niklause Wirtha z [6] do jazyka Rexx. H: procedure expose A. parse arg N, K L = 1; R = N do while L < R   X = A.K; I = L; J = R   do until I > J     do while A.I < X; I = I + 1; end     do while X < A.J; J = J - 1; end     if I <= J then do       W = A.I; A.I = A.J; A.J = W       I = I + 1; J = J - 1     end   end   if J < K then L = I   if K < I then R = J end return Analýza algoritmu H     Složitost algoritmu budeme posuzovat z počtu porovnání, jako je A.I < X a z počtu výměn W = A.I; A.I = A.J; A.J = W. Nechť C(N, K) označuje počet porovnání a S(N, K) počet výměn nutných při provádění programu H k nalezení K-tého nejmenšího z N prvků.     V nejhorším případě je: Cmax(N, 1) = Cmax(N, N) = (N2 + 5N - 8) / 2 Cmax(N, K) = (N2 + 5N - 12) / 2, for K = 2, 3, ..., N - 1     V [3] ukazuji příklady polí, které vedou k nejhoršímu případu (prvek v K-té pozici je označen červeně): for K = 1:    N    2    1    3    ...    N-1 for K = 2:    1    N     2    3    ...    N-1 for K = 3:    3    2    N    1    4    5    ...    N-1 for 3 < K < N-1:    2    ...      K-2     K    K-1    N    1    K+1    ...    N-1 for K = N - 1:    2    ...    N -1    1    N for K = N:    2    ...     N-2    N    N-1    1       V průměrném případě platí podle D. E. Knutha [2]: C(N, K) = 2((N + 1)HN - (N - K + 3)HN - K + 1 - (K + 2)HK + N + 3)     kde HN = 1 + 1/2 + ... + 1/N     V speciálních případech tedy platí: C(N, 1) = C(N,N) = 2N + o(N) C(N, median)= 2N(1 + ln2) + o(N) = 3.39N + o(N)     Já jsem odvodil vzorec pro určení průměrného počtu výměn: S(N, K) = (1 / 3)((N + 1)HN - (N - K + 2.5)HN - K + 1- (K + 1.5)HK + N + 2)     Důsledek: S(N, 1) = S(N,N) = HN S(N, medián) = (1 / 3) ((ln2 + 1)N - 3lnN) = 0.56N + o(N) Algoritmus Z      Uvažme pole 1, 10, 2, 3, 4, 5, 6, 7, 8, 9, a K = 2. Pole se rozdělí výše uvedeným postupem na dvě části A[1], ..., A[9] a A[10]: 1, 9, 2, 3, 4, 5, 6, 7, 8, 10 pomocí jedné výměny a 12-ti porovnání. Zjistím-li však, že 10 je větší než dva prvky (1 a 9), pak už přece vím, že nemůže být druhým nejmenším prvkem, a další porovnání jsou tedy zbytečná. Stejného výsledku (1, 9, 2, 3, 4, 5, 6, 7, 8, 10) dosáhnu jen s pomocí jedné výměny a třech porovnání. A pak mohu hned přejít na řešení redukované úlohy najít v poli A[1], ..., A[9] druhý nejmenší prvek. Modifikaci algoritmu H, pracující tímto způsobem, popisuje následující program Z. Je překladem mého programu z [3] do jazyka Rexx. Z: procedure expose A. parse arg N, K L = 1; R = N do while L < R   X = A.K; I = L; J = R   do until J < K | K < I     do while A.I < X; I = I + 1; end     do while X < A.J; J = J - 1; end     W = A.I; A.I = A.J; A.J = W     I = I + 1; J = J - 1   end   if J < K then L = I   if K < I then R = J end return Analýza algoritmu Z     V nejhorším případě: Cmax(N, K) = NK + N + K - K2 - 1, for K = 1, 2, ..., N U algoritmu Z maximální počet porovnání závisí na K. Následující graf ukazuje naměřenou dobu výpočtu H a Z v nejhorším případě.     V [3] jsem uvedl jen odhady pro průměrnou hodnotu C(N, 1), C(N, N) a S(N, K): C(N, 1) = C(N, N) = N + HN S(N, K) = 0.5((N + 1)HN - (N - K)HN - K + 1 - (K - 1)HK)      V speciálním případě tedy: S(N, 1) = S(N,N) = lnN + o(N) S(N, medián) = 0.5(Nln2 + 2lnN) + o(N) = 0.35N + o(N) Algoritmus FR Ve svém článku Expected Time Bounds for Selection [4] R. W. Floyd a R. L. Rivest popsali nový, efektivní algoritmus. Počet porovnání je v průměrném případě roven N + min(K, N - K) + o(N). Následující program FR je mým překladem původního programu z [5] do jazyka Rexx. FR: procedure expose A. parse arg L, R, K do while R > L   if R - L > 600 then do     N = R - L + 1; I = K - L + 1; Z = LN(N)     S = TRUNC(0.5 * EXP(2 * Z / 3))     SD = TRUNC(0.5 * SQRT(Z * S * (N - S)/N) * SIGN(I - N/2))     LL = MAX(L, K - TRUNC(I * S / N) + SD)     RR = MIN(R, K + TRUNC((N - I) * S / N) + SD)     call FR LL, RR, K   end   T = A.K; I = L; J = R   W = A.L; A.L = A.K; A.K = W    if A.R > T then do; W = A.R; A.R = A.L; A.L = W; end    do while I < J      W = A.I; A.I = A.J; A.J = W     I = I + 1; J = J - 1     do while A.I < T; I = I + 1; end     do while A.J > T; J = J - 1; end   end   if A.L = T then do; W = A.L; A.L = A.J; A.J = W; end     else do; J = J + 1; W = A.J; A.J = A.R; A.R = W; end   if J <= K then L = J + 1   if K <= J then R = J - 1 end return     Floyd a Rivest v [5] píší: Konstanty 600, 0.5, 0.5, vykytující se v popisu algoritmu, minimizovaly dobu výpočtu na používaném počítači. Ověřil jsem experimentálně, že hodnoty 600, 0.5, 0.5 jsou dobrým výběrem. U klasického Rexxu je tu problém s funkcemi LN, EXP a SQRT, protože nejsou součástí jazyka. Stovky experimentů ukázaly, že pro N = 10000 vystačíme s přesností výpočtu určenou příkazem numeric digits 6. Proto jsem použil algoritmy známé z učebnic: EXP: procedure parse arg Tr; numeric digits 3; Sr = 1; X = Tr do R = 2 until Tr < 5E-3   Sr = Sr + Tr; Tr = Tr * X / R end return Sr SQRT: procedure parse arg X; numeric digits 3 if X < 0 then return -1 if X=0 then return 0 Y = 1 do until ABS(Yp - Y) <= 5E-3   Yp = Y; Y = (X / Yp + Yp) / 2 end return Y LN: procedure parse arg X; numeric digits 3 M = (X + 1) / (X - 1); Ln = 1 / M do J = 3 by 2   T = 1 / (J * M ** J)   if T < 5E-3 then leave   Ln = Ln + T end return 2 * Ln     Experimentálně jsem zjistil, že nejrychleji výpočet proběhne, vydáme-li ve výše uvedených procedurách příkaz numeric digits 3 a srovnáváme-li hodnotu právě vypočteného členu s hodnotou 5E-3. Pro určení co nejmenšího počtu porovnání jsem ale jednoznačně nejlepší hodnoty těchto konstant nenašel. Někdy byla nejúspěšnější volba konstant 3 a 5E-3, jindy 4 a 5E-3, jindy zase 5 a 5E-5 nebo 6 a 6E-6. Nakonec jsem použill hodnoty 3 a 3E-5, s kterými byl výpočet zároveň nejrychlejší. Výsledek průměrného počtu porovnání při nalezení mediánu, 1.5N v dále uvedeném grafu, ukazuje, že program FR s těmito hodnotami pracuje podle očekávání. Porovnání algoritmů     Pro porovnání jsem použil program COMPARISON. Dále uvedený zjednodušený příklad tohoto programu měří jen dobu výpočtu pro hodnoty K >= 500. /* COMPARISON */ N = 10000 do K = 500 to 5000 by 500   TH = 0; TZ = 0; TFR = 0   do Trial = 1 to 100     call RANDARRAY; call INITIALIZE     call TIME "R"; call H N, K; TH = TH + TIME("R")     call INITIALIZE; call TIME "R"; call Z N, K     TZ = TZ + TIME("R"); call INITIALIZE     call time "R"; call FR 1, N, K     TFR = TFR + TIME("R")   end Trial   say K TH/100 TZ/100 TFR/100 end K exit RANDARRAY: procedure expose B. N do J = 1 to N; B.J = RANDOM(1, 100000); end return INITIALIZE: procedure expose A. B. N do J = 1 to N; A.J = B.J; end return     První graf ukazuje, že Z je rychlejší než FR jen pro K = 1. Mnohokrát jsem opakoval měření, abych si potvrdil, že algoritmus FR vyžaduje méně operací porovnání pro nalezení mediánu, a spotřebuje proto i méně času, než pro nalezení prvku, který je v pořadí podle velikosti 3000. nebo 4000.     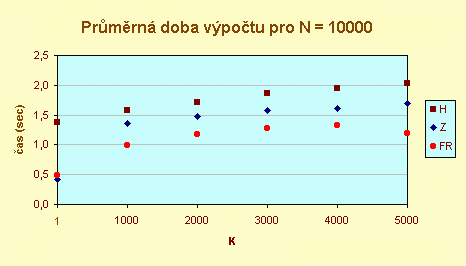Druhý graf porovnává počet porovnání (povšimněte si anomálie týkající se nižšího počtu operací porovnání u mediánu). Graf zároveň ukazuje, že Knuthův odhad pro průměrný počet operací porovnání u algoritmu H je správný. Algoritmus Z je nejlepší pro K = 1 a je o něco lepší než H; ale jasným vítězem v této kategorii je FR. Graf konečně dokazuje, že implementace v jazyce Rexx SELECTu neublížila - pro výpočet mediánu je opravdu v průměru zapotřebí jen 1.5N porovnání.     Poslední graf ukazuje, že Z potřebuje v průměru nejméně výměn. Navíc ukazuje, že můj odhad hodnoty S(N,K) pro Z je přesný. Závěr Algoritmy Z a FR jsou vždy lepší než H; FR provede v průměru méně operací porovnání než Z; Z provede v průměru méně výměn než FR. Další informace uvádím v článku O algoritmu MODIFIND. Komentář Richarda Hartera v comp.programming To je zajímavé. K přitažlivým vlastnostem algoritmu Z patří jeho jednoduchost. To není maličkost. Při výběru algoritmu často srovnáváme jeho časovou složitost s dobou strávenou na jeho kódování a ladění. V každém případě je hezké mít tyto algoritmy k dispozici on-line.   Richard Harter, cri@tiac.net, The Concord Research Institute http://www.tiac.net/users/cri   Jaký je rozdíl mezi civilním a vojenským inženýrem? Vojenský staví zbraně, civilní cíle.   Literatura   1. C. A. R. HOARE: Proof of a Program: FIND. CACM, Vol 14, No. 1, January 1971, pp. 39-45. 2. D. E. KNUTH: The Art of Computer Programming. Sorting and Searching. Addison-Wesley, Reading, Mass., 1973. 3. V. ZÁBRODSKÝ: Variace na klasické téma. Elektronika, No. 6, 1992, pp. 33-34. 4. R. W. FLOYD, R. L. RIVEST: Algorithm 489 The Algorithm SELECT - for Finding the ith Smallest of n Elements [M1]. CACM, March 1975, Vol. 18, No. 3, p. 173. 5. R. W. FLOYD, R. L. RIVEST: Expected Time Bounds for Selection. CACM, March 1975, Vol. 18, No. 3, pp. 165-172. 6. N. WIRTH: Algorithms and data structures. New Jersey 07632, Prentice Hall, Inc., Engelwood Cliffs, 1986.