Indietro | Home | Avanti

Introduzione | Cap.1 | Cap.2 | Cap.3 | Cap.4 | Cap.5 | Appendice | Bibliografia

Esaminiamo adesso piu' da vicino due algoritmi che tracciano curve di livello, precisamente TRICP [A1] e FARB-E-2D [A2], presi a campione per confrontare le diverse filosofie di base. Il primo, infatti, opera su dati distribuiti irregolarmente, mentre le funzioni locali sono polinomi di 5° grado di due variabili. Il secondo opera su dati distribuiti regolarmente e le funzioni locali sono polinomi (di 6° grado) di Hermite.

Abbiamo scelto di restringere la nostra analisi soltanto a questi dal momento che:

1) altri algoritmi meno recenti (GCONTR,CNTOUR), sebbene utili in molti problemi particolari, risentono ormai del peso degli anni;

2) solo per questi algoritmi e' possibile un implementazione parallela;

Piu' avanti, comunque, viene data una breve descrizione di GCONTR [A3] l' algoritmo che rappresenta il modo tradizionale di tracciare curve di livello.

L' algoritmo TRICP utilizza uno schema di interpolazione che si basa su polinomi di quinto grado di due variabili per ogni triangolo. La funzione interpolante e' differenziabile con continuita' attraverso i lati dei triangoli e, accanto ai valori della funzione, sono assunte nei punti dati le derivate prime e seconde. Le formule per il calcolo dei coefficienti dei polinomi sono quelle sviluppate da Akima [B2] ed utilizzate dallo stesso autore nell' algoritmo 526 dell' ACM [B2].

Basandosi sulle idee di Akima l' algoritmo TRICP implementa un metodo alternativo per trovare le linee di livello che e' stato, fino, ad oggi considerato troppo complesso e costoso da usare in pratica: la soluzione successiva di equazioni non lineari per trovare i punti di una curva di livello. Il metodo su cui si basa evidenzia le caratteristiche della funzione interpolante. Infatti dal momento che ogni punto plottato e' valutato direttamente da questa funzione, che e' continua e smooth, le linee di livello che ne risultano saranno in genere smooth. Le distanze tra i punti sono scelte opportunamente brevi in modo che ogni punto puo' essere unito al successivo da una linea retta. Questa e' l' unica interpolazione che avviene in aggiunta alla determinazione della funzione interpolante di due variabili. Cosi', ogni punto plottato riflette la vera forma della superficie interpolante. Quindi, le linee di livello passeranno per i punti della stesso valore, e le linee di contorno di differenti livelli non potranno intersecarsi. Il tempo di calcolo non e' influenzato dal numero dei punti della griglia, ma dipende dalla lunghezza e dalla forma delle linee plottate.

L' algoritmo si basa sui seguenti passi:

i)calcolo dei coefficienti del polinomio di quinto grado che rappresenta la funzione interpolante lungo i tre lati del triangolo. La formula per il polinomio sul terzo lato e' stata aggiunta alla formula di Akima.

ii)calcolo sui tre lati della posizione dei punti in cui le derivate prime ed i rispettivi polinomi sono uguali a zero. I polinomi vengono valutati su questi punti. Vengono determinati gli estremi dei polinomi lungo i lati, tenendo conto dei valori su questi punti e dei vertici.

iii)calcolo degli zeri delle funzioni che sono definite come differenze tra le linee di livello e i polinomi lungo ciascuno dei tre lati . I punti trovati in ii) vengono usati come punti iniziali per le iterazioni. Gli zeri trovati sono i punti in cui le linee di livello attraversano i lati del triangolo.

iv)se vengono trovati punti di questo tipo, viene calcolata la rappresentazione del polinomio all' interno del triangolo.

v)calcolo consecutivo dei punti di una linea di livello che iniziano e terminano sui punti trovati al passo iii). Ogni punto di una linea e' calcolato come zero di una funzione di una variabile.Questa funzione e' definita lungo una linea retta che e' normale alla tangente alla curva, ad una certa distanza dall' ultimo punto calcolato. La forma analitica di questa funzione non viene determinata; i valori sono presi dal polinomio di due variabili in iv).

Segue una descrizione dettagliata dei passi riportati. Prima di tutto l' algoritmo e' organizzato in modo che ogni triangolo e' processato separatamente. Cio' semplifica il processo permettendo di evitare di seguire una linea attraverso tutti i triangoli incontrati. In particolare evita la scelta, impegnativa dal punto di vista del tempo di calcolo, di quali coefficienti del polinomio utilizzare. Da questo primo principio base segue anche che i punti calcolati sui lati che separano due triangoli vengono calcolati due volte, uno per ogni triangolo. Questo e' un prerequisito indispensabile per operazioni parallele su tutti i triangoli allo stesso tempo.

Il secondo principio riguarda il controllo delle linee di livello. La ricerca degli zeri e' limitata ai lati dei triangoli per ragioni di efficienza. La stessa strategia come descritta dai passi (i)-(iii) potrebbe anche essere usata lungo alcune linee all'interno del triangolo. Quindi, con l'algoritmo presentato, le linee di livello chiuse all' interno di un triangolo non possono essere determinate. Cio' e' considerato accettabile, in quanto solo linee trascurabili e brevi sono di questo tipo. Inoltre, il valore di un estremo all' interno di un triangolo, distante da un punto dato, e' difficile da determinare per interpolazione e piuttosto impreciso. Se la posizione dei punti dati in un problema puo' essere scelta, e non puo' essere usata una griglia rettangolare, si puo' sempre tentare di posizionare i punti piu' vicini possibile all' estremo. Cosi' e' abbastanza probabile che tutte le linee di livello richieste attraversano i lati dei triangoli. Se cio' non capita, allora si puo' considerare una differente triangolazione in modo che un lato di un triangolo attraversa l' area in cui e' importante trovare tutte le linee di livello. Naturalmente la funzione interpolante non e' invariante per simili modifiche.

La terza considerazione e' che il metodo richiede che le coordinate x e y usate per il disegno siano introdotte all' inizio della procedura. Questo e' necessario per due motivi. Uno degli obiettivi dell' algoritmo e' di produrre linee smooth e di approssimare il corso di una linea di livello esattamente com'e' richiesto per scopi di disegno. Quindi, il numero di punti calcolati per linea puo' cambiare se vengono usate scale differenti. Per plottaggi di grandi dimensioni, devono essere calcolati piu' punti. In secondo luogo, uno dei criteri di arresto nelle computazioni iterative e' che venga raggiunta una certa precisione. Quindi, la precisione relativa in plottaggi di grandi dimensioni deve essere piu' alta e puo' impiegare piu' tempo per essere raggiunta. Il fatto che il tempo di calcolo dipende dalla scala del disegno rivela la proprieta' base del metodo che e' differente dalla maggior parte degli algoritmi di disegno di contorni esistenti in letteratura. Vediamo adesso con quali metodi le strategie discusse sono state realizzate.

La difficolta' principale nel calcolare zeri successivi di una funzione non lineare e' trovare uno zero che appartiene ad una designata sequenza di zeri (curva di livello) e non ad un' altra. A tale scopo, devono essere usati dei metodi di predizione per calcolare i valori iniziali per la prossima iterazione. Deve essere garantito ad ogni passo che il valore iniziale porti ad uno zero accettabile. A tal proposito non e' possibile raggiungere una assoluta affidabilita', in quanto la ricerca per il prossimo zero deve essere condotta ad una certa distanza dall' ultimo. In termini delle linee di livello, per esempio, questo significa che in casi limite linee dello stesso livello possono incrociarsi, sebbene dal punto di vista algebrico dovrebbe esserci una piccola distanza fra loro. Per questo motivo questo algoritmo non e' adatto per mostrare la struttura topologica di funzioni polinomiali correttamente in tutte le situazioni.

Una prima difficolta' si incontra nei triangoli molto sottili. Questo poteva essere atteso in quanto viene determinato un polinomio di 5° grado per ogni triangolo quale che sia la sua forma. Quindi, e' stato introdotto un parametro "h min" per l' altezza minima accettabile per i triangoli. Quando h min e' piu' piccolo di un certo valore, la precisione dei punti calcolati e la distanza massima fra di essi dipende da questo parametro. Dal momento che il calcolo delle linee di livello dura a lungo, triangoli molto sottili dovrebbero essere evitati. Determinata la precisione, vengono calcolati lungo i lati i coefficienti dei polinomi del 5° ordine. Il calcolo dei coefficienti per due lati e' parte della procedura di Akima [B2]. Nel metodo tradizionale essi sono necessari soltanto per la valutazione del polinomio di due variabili all' interno del triangolo. I coefficienti per il terzo lato possono essere trovati cambiando ad un vertice differente l' origine di un sistema locale di coordinate. Il massimo e il minimo per ogni lato sono determinati per mezzo dei coefficienti delle derivate dalla 1a alla 4a di questi polinomi. Se un dato livello e' sopra il massimo o sotto il minimo di tutti i lati, cio' significa che la linea di livello non attraversa il triangolo che viene scartato per questo livello. Altrimenti, considerando i punti estremi di un lato e i punti in cui le derivate prime si annullano lungo tale lato, viene determinato l' intervallo in cui la funzione di interpolazione incrocia la linea di livello. Gli estremi di questo intervallo sono usati come punti iniziali per la ricerca di una radice locale. Il punto trovato e' preso come il primo o l' ultimo punto della linea di livello. Quando viene cominciata una linea, la sua direzione e' stimata approssimando con un piano la superficie interpolante nel primo punto. A questo scopo, usiamo la derivata prima nella direzione del lato.

Una volta che e' stata determinata la direzione iniziale, possono essere calcolati i punti successivi della linea di livello. Dal momento che questa e' la parte centrale dell' algoritmo, spieghiamo questo processo in dettaglio.

Come gia' detto, i punti calcolati possono essere visti come zeri di funzioni definite normali alla attuale direzione della curva. Sia f(x,y) la funzione interpolante per il triangolo e c e' la quota della curva di livello. Le coordinate (x,y) di un punto p di una linea di livello, devono verificare la f(x,y)-c=0. (1)

Per ogni punto p viene stimato preliminarmente un punto f di coordinate xf ,yf . I punti p sono cercati lungo le linee per cui valgono le seguenti equazioni:

x(r) = xf + cos(J)´ r (2a)

y(r) = yf + sin(J)´ r (2b)

dove r e' una variabile in direzione normale alla curva; cos(J) e sin(J) definiscono questa direzione; xf e yf sono estrapolati dalle coordinate degli ultimi tre punti p. Il punto F, stima del prossimo p, e' calcolato in questa direzione ad un' opportuna distanza ds dall' ultimo p; ds e' chiamato "step size".

Poiche' il punto F normalmente giace da un lato della curva e' facile trovare un secondo punto su una linea definita dall' eq. (2), su cui la (1) assume segno opposto. Se un punto di questo tipo non puo' essere trovato entro una certa distanza rmax dal punto F, cio' normalmente significa che la curvatura della linea di livello e' aumentata. Quindi lo step size ds e' ridotto di un fattore .5 fino a che non viene trovato un punto di questo tipo. Adesso il processo iterativo per calcolare il prossimo p come zero di una funzione di variabile r puo' cominciare usando l'eq. (1) e (2). Se l' r che risulta per p e' piu' piccolo di un certo valore rmin , allora lo step size ds e' raddoppiato per il passo successivo. In questo modo, rmax e rmin controllano lo step size ds e vengono prodotte linee smooth.

La velocita' di convergenza puo' essere misurata dal numero delle valutazioni della funzione necessarie per raggiungere la precisione richiesta. Necessita circa 5-6 valutazioni aggiuntive della funzione lungo i lati quando vengono trovati come punti iniziali due punti con segni discordi. Normalmente solo due valutazioni aggiuntive della funzione sono necessarie dentro il triangolo.

Osserviamo che la funzione interpolante usata e' differenziabile con continuita', non solo lungo i lati dei triangoli ma anche sugli stessi punti dati, cioe' i nodi della griglia triangolare. Questo implica che le derivate parziali seconde, così come le prime, siano specificate nei punti dati. Questo e' normalmente considerato uno svantaggio, in quanto la pendenza e la curvatura devono essere stimate dai valori della funzione, e deve essere fatta particolare attenzione per ottenere valori utili. D' altra parte, questi dati qualche volta hanno significato fisico e sono gia' disponibili. Inoltre, con sei parametri per punto, e' molto pratico costruire la superficie.

In conclusione i vantaggi principali del metodo proposto in confronto ai metodi tradizionali per il tracciamento di contorni con l' interpolante usato sono i seguenti:

1) e' metodologicamente piu' diretto e esatto, in quanto i punti plottati sono valutati direttamente dalla funzione interpolante.

2) richiede meno memoria e in casi normali meno tempo di calcolo.

Caratteristiche che potrebbero essere considerate svantaggi sono:

1) le linee di contorno sono create a tratti.

2) le linee di livello che non attraversano i bordi dei triangoli non vengono scoperte.

L' algoritmo FARBE, a differenza di TRICP, utilizza come funzione interpolante polinomi di Hermite di sesto grado. I polinomi di Hermite sono ben conosciute ed ampiamente utilizzate per la definizione di superfici su griglie rettangolari. Sedici valori ai vertici di ogni rettangolo individuano univocamente 16 coefficienti di un polinomio di Hermite di due variabili . Questi valori sono le coordinate z, le due derivate parziali zx,zy , e le derivate miste zxy. Il polinomio e' del terzo ordine su linee parallele agli assi coordinati e del sesto ordine in tutte le altre direzioni. Per il calcolo delle derivate parziali viene usato il metodo di Akima gia' presentato, comunque il terzo livello dell' interfaccia utente e' stato progettato in modo che l' utente possa fornire i propri valori per le derivate.

Il programma permette di colorare le aree tra le linee di livello. Ripetiamo brevemente le linee generali del Trip Algorithm. Esso descrive come si possono trovare i punti, che definiscono aree di differenti colori o retini fra due linee di livello, per interpolazione di funzioni non lineari dentro un dominio delimitato da confini lineari. In FARB-E-2D, la funzione e' il polinomio di sesto grado, ed il dominio un rettangolo. Dapprima, i punti di intersezione S dei contorni con i lati di un rettangolo sono calcolati come zeri delle funzioni di terzo grado f-ci , dove f e' la funzione interpolante sulle linee della griglia e ci la linea di livello. Questi zeri sono chiamati stazioni S. Invece di calcolarli livello per livello per ogni lato, vengono generati in sequenza topologica. Vengono ordinati in senso antiorario sui lati. Per ogni stazione, in direzione antioraria dei lati, vengono immagazinati le linee di livello ci e le derivate prime di f . Il segno di questa derivata e la linea di livello definiscono i due differenti colori da dare alle aree sui lati della stazione. 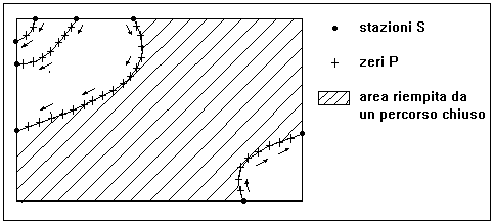Adesso (Fig.2.1) viene determinato un percorso non retto calcolando gli zeri P della funzione f-ci sulla linea di livello, dove f e' adesso la funzione interpolante di due variabili definita sul rettangolo. Noi chiamiamo questo processo un percorso in quanto essa collega due stazioni dello stesso livello. Come in TRICP gli zeri P sono cercati col metodo della regula falsi su linee normali al vettore tangente alla curva ottenuta .La deviazione dalla tangente e dagli altri parametri locali determina la dimensione del passo. La dimensione e' rappresentata dalla distanza ,in cui giace la prossima linea di ricerca. A differenza dell' algoritmo TRICP ci si assicura che la derivata normale (perpendicolare alla curva) non cambia di segno durante un percorso. Cio' evita l'intersecarsi di curve in vicinanza di punti a sella.

FIG.2.1- IL Trip Algorithm CALCOLA POLIGONI PIENI PER INTERPOLAZIONE NON LINEARE DI FUNZIONI. QUESTA E' UNA SITUAZIONE TIPICA SU UN RETTANGOLO FORMATO DALLE LINEE DELLA GRIGLIA.

Dopo aver raggiunto una stazione termina un percorso, quindi viene compiuto un trasferimento lungo i lati fino alla prossima stazione , dove comincia un nuovo percorso fino a qunando non viene compiuto un ciclo chiuso (round trip) e viene raggiunta la stazione di partenza del percorso. I trasferimenti vengono compiuti sui lati in direzione antioraria. Se necessario al poligono vengono aggiunti i vertici del rettangolo durante un trasferimento. Il percorso coprira' l' intera area del rettangolo quando tutte le stazioni sono usate due volte, una volta come inizio e una come fine del percorso. I punti P di ciascun percorso trovato vengono tenuti in uno stack in quanto essi spesso sono parte di un percorso adiacente .In ogni caso questi punti torneranno utili in ordine inverso. La Fig.2.1 illustra il Trip Algorithm.

Vogliamo fissare adesso l' attenzione su alcuni problemi numerici che si presentano in questo algoritmo. Una classe di problemi e' comune a tutti gli algoritmi che tentano di trovare il corso di una curva algebrica per mezzo di metodi puramente numerici. Per tracciare le curve, sono determinati un numero finito di punti con precisione limitata. Questo si verifica in quanto non e' possibile conoscere in anticipo la struttura topologica della curva . Cosi' e' teoricamente possibile che il processo di tracciamento salti ad un altro ramo della curva, che puo' persino essere una linea chiusa o una parte gia' incontrata di un percorso. In questo modo possono verificarsi viaggi che non possono essere completati. Questi eventi indesiderati non possono essere completamente evitati, ma la loro ricorrenza puo' essere resa piu' difficile con una attenta selezione dei parametri locali nel processo di ricerca. In FARB-E-2D, questo e' fatto automaticamente; l' utente non ha bisogno di esserne a conoscenza . Un altro problema e' che noi implicitamente assumiamo che la curva di un percorso sia continua e smooth. Questa supposizione e' permessa in tutti i casi eccetto uno: nei punti a sella, cioe' se deve essere tracciata la linea di livello su un punto a sella. In punti di questo tipo, in cui le linee dello stesso livello si intersecano, un percorso deve cambiare direzione in modo discontinuo in modo da evitare percorsi che attraversano se stessi che porterebbero ad avere alcune aree vuote se abbiamo scelto l' opzione per il riempimento delle aree. In questa situazione e' di aiuto la scelta di un segno costante per la derivata normale di un percorso: il percorso non continuera' nella stessa direzione verso l'altro lato del punto a sella. Si fermera' o prendera' la giusta direzione . Se si ferma la direzione della linea di ricerca viene cambiata di 90 gradi, e viene ripetuta la ricerca per una continuazione corretta.

Il calcolo delle stazioni S puo' anche risultare mal condizionato in quanto una linea di livello puo' interamente o in parte coincidere con un lato di un rettangolo. In questi casi, la posizione di S e' indefinita, e procedure diverse possono portare a risultati differenti. Cosi' potrebbe essere impossibile per un percorso trovare il suo giusto termine, oppure esso potrebbe addirittura non cominciare. L' affidabilita' dell' algoritmo in questi casi e' stata accresciuta aggiungendo alcune estensioni alla procedura base dascritta. Ripetiamo alcune di queste. Si permette per esempio che un percorso finisca tra due stazioni vicino ad un lato. E soprattutto, se un percorso non puo' essere terminato con successo, esso viene lanciato di nuovo da un altra stazione. Se infine vengono raggiunte stazioni che sono state usate una volta sola, i percorsi potrebbero anche cominciare in direzione oraria. Inoltre, quando sono attesi valori vicini allo zero, vengono usate le differenze per determinare il segno delle derivate invece di valutare il polinomio. Cio' dovrebbe eliminare gli effetti di errori di arrotondamento sul segno.

Problemi di questo tipo si presentano raramente nei grafici che risultano da simulazioni numeriche di fenomeni naturali o di ingegneria , per esempio, nella soluzione di equazioni differenziali alle derivate parziali. Comunque nel modellamento di superfici o quando i valori sulla griglia sono interi, queste situazioni si possono presentare facilmente se vengono scelti valori particolari per le linee di livello. Come per l'algoritmo TRICP le linee di livello chiuse all' interno di un rettangolo non vengono trovate per il fatto che i punti di partenza S sono ricercati soltanto sui lati dei rettangoli.

Per quanto riguarda l' implementazione, per l' algoritmo e' stata progettata un interfaccia utente a tre livelli. Per accedere al primo e piu' alto livello, un utente ha bisogno soltanto di fornire una matrice bidimensionale Z, contenente i valori Zij nei punti della griglia, la dimensione del suo primo indice NXDIM, e i limiti NX e NY dei due indici ad una subroutine di nome FARBE (i=1,NX j=1,NY). Una chiamata di questo tipo dovrebbe apparire come

call FARBE(Z,NXDIM,NX,NY,MODE)

Per default MODE dovrebbe essere posto a zero. Il programma si prende cura della scalatura e della selezione di linee di livello convenienti. Il risultato sara' un completo disegno di linee di livello con contorni pieni. I differenti colori o retini usati per le aree fra le linee di livello sono identificabili per mezzo di una legenda che verra' disegnata automaticamente. Chiamando FARBE, il risultato sara' sempre una griglia di forma quadrata , perfino se NX¹NY. I due indici della matrice determinano la posizione dei valori Z alle intersezioni delle linee della griglia , rispettivamente in direzione x e y. Se la forma del disegno dovrebbe apparire come un rettangolo oppure l' utente vuole spacificare esplicitamente le linee della griglia, deve essere utilizzata una chiamata a FARB2D (secondo livello). La scalatura delle coordinate x e y deve essere compiuta dall' utente e devono essere forniti anche i valori delle linee di livello. Una chiamata a FARB2D e' del tipo

call FARB2D(X,NX,Y,NY,Z,NXDIM,CN,ICOL,NC,MODE)

dove i vettori X e Y di lunghezza NX e NY danno rispettivamente le coordinate delle linee della griglia, CN sono i valori delle linee di livello in ordine ascendente , e i valori (interi) di ICOL rappresentano i colori scelti o i retini per le NC-1 differenti aree fra le linee di livello (NC= numero delle linee di livello ). Il primo valore ICOL(1) del vettore ICOL di lunghezza NC+1 e' usato per le aree al di sotto della prima linea di livello CN(1), L' ultimo ICOL(NC+1), per le aree oltre il piu' alto livello CN(NC). Il parametro MODE indica se e' richiesto un puro tracciamento di linee, o riempimento delle aree o entrambi. Scegliendo il primo livello, l'utente riceve il controllo su ogni singolo rettangolo formato dalle linee della griglia. Cosi' l'utente puo' specificare tutti i valori ai vertici del rettangolo che sono necessari per costruire le funzioni locali. In teoria i calcoli per tutti i rettangoli potrebbero essere eseguiti in parallelo in quanto non ci sono legami fra di essi, quando tutti i valori ai nodi sono stati calcolati. Comunque, l' algoritmo implementa un' opzione che risparmia tempo di calcolo sequenziale: se il prossimo rettangolo da processare e il confinante a destra dell' ultimo, la posizione delle stazioni S del lato in comune non vengono ricalcolate.

Dando una matrice bidimensionale modello di una superficie, i valori di livello, la subroutine GCONTR determina la successione di punti nel piano che possono essere usati per tracciare contorni attraverso i punti della superficie che hanno stessi valori.

GCONTR e' del tipo che segue i contorni. Su un problema tipico, un programma che usa l' algoritmo GCONTR genera 11.000 comandi plotter contro i 57.000 comandi generati da un programma che usa il metodo a celle. Esso usa l' interpolazione per stimare i punti in cui una linea di livello interseca il bordo di una cella. Una volta determinati i punti di intersezione di un contorno con i bordi essi vengono uniti con linee rette. GCONTR implementa un mezzo con il quale l' utente puo' indicare elementi della matrice da escludere. I lati che collegano elementi esclusi con elementi non esclusi non vengono esaminati. Questa caratteristica e' stata trovata molto utile in pratica, in cui i dati sono frequentemente non forniti su una griglia rettangolare completa. Quando si usano metodi che non hanno questa caratteristica, si trovano frequentemente disegnati contorni estranei fra le regioni che contengono i dati e le regioni che non ne contengono.

Per migliorare l' output del programma si potrebbe utilizzare una seconda procedura di interpolazione non lineare per il disegno delle linee (tecnica di smoothing). Ma questo comporterebbe che le linee plottate non corrispondono piu' strettamente alla superficie interpolante determinata. Inoltre se lo smoothing e' eseguito senza attenzione puo' capitare che linee di diverso livello si intersechino.

Indietro | Home | Avanti

Introduzione | Cap.1 | Cap.2 | Cap.3 | Cap.4 | Cap.5 | Appendice | Bibliografia