Umberto Marzo - Tesi di Laurea

Introduzione | Cap.1 | Cap.2 | Cap.3 | Cap.4 | Cap.5 | Appendice | Bibliografia

CAPITOLO 3

L' Algoritmo Contour

Per verificare la possibilita' di implementare in parallelo gli algoritmi per il tracciamento di linee di livello e studiarne le prestazioni e' stato realizzato dall' autore un programma che implementa le idee esposte nei paragrafi precedenti. Piu' precisamente il programma implementa un algoritmo cellulare, per dati distribuiti ai nodi di una matrice rettangolare, usando come funzioni locali piani che approssimano il comportamento della superficie. L' equazione analitica di questi ultimi non viene determinata dal momento che sono necessarie soltanto le posizioni dei punti in cui questi intesecano le linee di livello sui lati del rettangolo. E' sufficiente quindi determinare l'equazione della retta che passa per gli estremi di ciascun lato e da questa stimare la posizione in cui la linea di livello interseca il lato.

Segue il listato commentato del programma.

dichiarazione dei sottoprogrammi (Sub) e delle funzione (Function) utlizzate.

DECLARE SUB legenda (n%, c!())

DECLARE SUB lato (i%, j%, m%, n%, c!, x!, y!, flag%)

DECLARE SUB rettangolo (i%, j%, c(), col%(), numlin%)

DECLARE FUNCTION funz! (x!, y!)

DECLARE FUNCTION interp (x1, z1, x2, z2, c)

dimensionamento delle matrici e dei vettori.

grid e' la matrice bidimensionale che contiene i dati della superficie da interpolare

xdim,ydim indicano il numero di righe e colonne della matrice grid.

col il vettore che rappresenta i colori da assegnare alle linee di livello.Esso viene condiviso (Shared) dalla routine principale e dalla sub Legenda.

c e' il vettore che contiene le linee di livello.

DIM grid(100, 100), xdim AS INTEGER, ydim AS INTEGER

DIM xdim1 AS INTEGER, ydim1 AS INTEGER

DIM SHARED col(1 TO 15) AS INTEGER, c(1 TO 14)

Sezione di input.Viene chiesto all' utente il dominio su cui campionare la funzione, il numero delle linee di livello ed i loro valori. Viene eseguito un controllo sui dati immessi per evitare errori.

CLS

PRINT "dominio in cui campionare la funzione:"

INPUT "intervallo delle ascisse (a,b) "; xx, xx1

INPUT "intervallo delle ordinate (c,d)"; yy1, yy

IF xx >= xx1 OR yy1 >= yy THEN RUN

INPUT "num. punti sulle x"; xdim

INPUT "num.punti sulle y"; ydim

INPUT "numero di linee di livello (max 14)"; numlin%

PRINT "vettore delle linee di livello"

FOR i% = 1 TO numlin%

INPUT c(i%)

NEXT i%

SCREEN 12

hx e hy contengono le misure dei lati dei rettangoli della reticolazione

hx = (xx1 - xx) / (xdim - 1)

hy = (yy1 - yy) / (ydim - 1)

gridcol% = 15

definizione delle variabili per l'ingrandimento opportuno del grafico e per la sua centratura sullo schermo

zoomx = 300 / ABS(xx1 - xx)

zoomy = 300 / ABS(yy1 - yy)

specular = 240 + (yy - (ABS(yy1 - yy) / 2)) * zoomy

specularx = 320 - (xx + (ABS(xx1 - xx) / 2)) * zoomx

definizione di un vettore per i colori delle linee di livello e costruzione della legenda

CALL legenda(numlin%, c())

costruisce una reticolazione del dominio in base ai dati forniti. I valori ai nodi della griglia sono forniti dalla funzione FUNZ

ydim1 = ydim - 1

xdim1 = xdim - 1

FOR j% = 0 TO ydim1

y = yy + hy * j%

FOR i% = 0 TO xdim1

x = xx + hx * i%

grid(j%, i%) = funz(x, y)

NEXT i%

NEXT j%

traccia il bordo del grafico

LINE (xx * zoomx + specularx, specular - yy * zoomy)-((xx + (xdim - 1) * hx) * zoomx + specularx, speculaar - ((yy + (xdim - 1) * hy) * zoomy)), gridcol%, B

GOTO 20 ' togli questa riga se vuoi anche la griglia

disegna la griglia sullo schermo:

assi orizzontali

FOR j% = 0 TO ydim - 1

LINE (xx * zoomx + specularx, specular - ((yy + j% * hy) * zoomy))-(xx1 * zoomx +specularx, specular - ((yy + j% * hy) * zoomy)), gridcol%, , 4681

NEXT j%

e verticali

FOR i% = 0 TO xdim - 1

LINE ((xx + i% * hx) * zoomx + specularx, specular - yy * zoomy)-((xx + i% * hx) * zoomx + specularx, specular - (yy1 * zoomy)), gridcol%, , 4681

NEXT i%

e finalmente si processano uno alla volta tutti i rettangolini che formano la griglia

FOR i% = 0 TO ydim - 2

FOR j% = 0 TO xdim - 2

CALL rettangolo((i%), (j%), c(), col%(), numlin%)

NEXT j%

NEXT i%

END

questa e' la definizione della funzione utilizzata per la costruzione della griglia. Sono comprese come commenti alcune funzioni da utilizzare per il test del programma.

FUNCTION funz (x, y)

' funz = x + y

' funz = 3 / 2 * (COS(3 / 5 * (y - 1)) + 5 / 4) / (1 + ((x - 4) / 3) ^ 2)

' funz = ABS(x + y)

funz = SIN(x ^ 2) + COS(y ^ 2) + SIN(x)

' funz = TAN(y - x) + 1

' funz = 8 / 3.14 * EXP(-8 * (x * x + y * y))

' funz = 9 * (3 / 4 * EXP(-(x - 3) ^ 2 - (y - 3) ^ 2) / 4) + EXP(-(x / 7) ^ 2 - (y / 10) - 1 / 5 * EXP(-(x - 5) ^ 2 - (y - 8) ^ 2) + 1 / 2 *

EXP((-(x - 8) ^ 2 - (y - 4) ^ 2) / 4))

END FUNCTION

questa function calcola per interpolazione lineare l'ascissa del punto di ordinata c (linea di livello). I parametri di input sono le ascisse dei punti (x1 e x2) ,le loro ordinate (z1 e z2) e la quota della linea di livello. L' output e' la posizione del punto rispetto ad un sistema di riferimento con origine in x1 in cui ,secondo l'interpolazione lineare, la linea interseca il lato.

FUNCTION interp (x1, z1, x2, z2, c)

IF (z2 - z1) = 0 THEN

interp = 0

ELSE

interp = (c - z1) * (x2 - x1) / (z2 - z1)

END IF

END FUNCTION

questa sub determina se la linea di livello specificata interseca questo lato e la posizione del punto relativamente al sistema di riferimento del grafico.

SUB lato (i%, j%, m%, n%, c, x, y, flag%)

SHARED hx, hy, grid()

IF (grid(i%, j%) <= c AND c <= grid(m%, n%)) OR (grid(m%, n%) <= c AND c <= grid(i%, j%)) THEN

x = j% * hx + interp(j% * hx, grid(i%, j%), n% * hx, grid(m%, n%), c)

y = i% * hy + interp(i% * hy, grid(i%, j%), m% * hy, grid(m%, n%), c)

flag% = 1

END IF

END SUB

Questa sub definisce il vettore dei colori da assegnare alle linee di livello e costruisce la legenda.

SUB legenda (n%, c())

SHARED col() AS INTEGER

col(1) = 8: col(2) = 7: col(3) = 3: col(4) = 11: col(5) = 2: col(6) = 10

col(7) = 14: col(8) = 13: col(9) = 5: col(10) = 4: col(11) = 9

col(12) = 1: col(13) = 6: col(14) = 15: col(15) = 12

SCREEN 12

a = 0

FOR i% = 1 TO n%

LINE (10, a + i% * 16)-(23, a + 16 + 16 * i%), col(i%), BF

LOCATE 2 * i%, 4

PRINT c(i%)

a = a + 16

NEXT i%

END SUB

Questa sub processa il rettangolino della griglia individuato dagli indici i e j.

SUB rettangolo (i%, j%, c(), col%(), numlin%)

SHARED xx, yy, specular, specularx, zoomx, zoomy

DIM x(1 TO 4), y(1 TO 4), flag%(1 TO 4)

FOR k% = 1 TO numlin%

CALL lato(i%, j%, i%, j% + 1, c(k%), x(1), y(1), flag%(1))

CALL lato(i%, j%, i% + 1, j%, c(k%), x(2), y(2), flag%(2))

CALL lato(i% + 1, j%, i% + 1, j% + 1, c(k%), x(3), y(3), flag%(3))

CALL lato(i% + 1, j% + 1, i%, j% + 1, c(k%), x(4), y(4), flag%(4))

FOR ii% = 1 TO 4

IF flag%(ii%) = 1 THEN

x1 = x(ii%)

y1 = y(ii%)

FOR jj% = ii% + 1 TO 4

IF flag%(jj%) = 1 THEN

x2 = x(jj%)

y2 = y(jj%)

END IF

NEXT jj%

LINE ((xx + x1) * zoomx + specularx, specular - (yy + y1) * zoomy)-((xx + x2) * zoomx + specularx, specular - (yy + y2) * zoomy), col%(k%)

END IF

NEXT ii%

flag%(1) = 0: flag%(2) = 0: flag%(3) = 0: flag%(4) = 0

NEXT k%

END SUB

NOTA. Il programma presentato e' stato realizzato in Basic. Comunque la sua traduzione in altri linguaggi non dovrebbe comportare particolari problemi dal momento che sono stati usati costrutti presenti in tutti i linguaggi di programmazione.

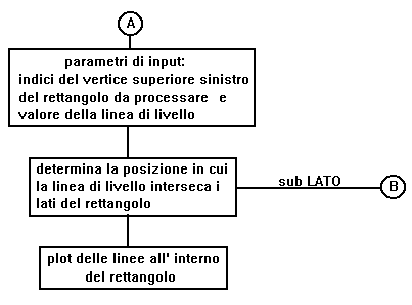
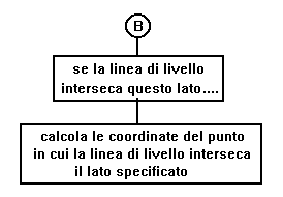
Diagramma di flusso programma CONTOUR

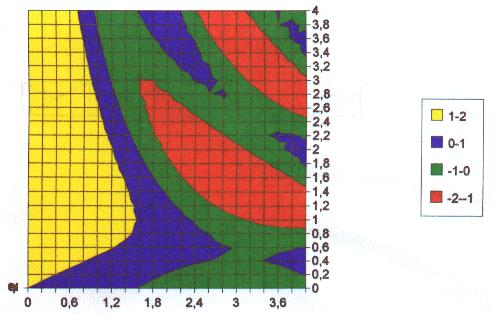
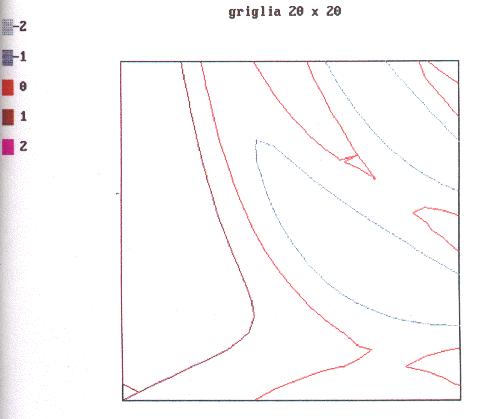
Le pagine che seguono mostrano alcuni esempi di output ottenuti con il programma Contour, per un dominio sempre piu' fitto di punti. La superficie utilizzata per il test del programma e' visibile in fig.3.1, mentre, in fig.3.2 e' riportato il risultato "esatto" per le linee di livello.

Indietro | Home | Avanti

Introduzione | Cap.1 | Cap.2 | Cap.3 | Cap.4 | Cap.5 | Appendice | Bibliografia