2.4.8 Interferometrie
 

(interferometric techniques)
 
Der Effekt einer faszinierend schillernden Oberfläche einer Seifenblase hat auch Anwendung in der Messtechnik gefunden.

Prinzip^xxii

nach [1 i)] [10] [11]

Abbildung 2.8: Interferometrie

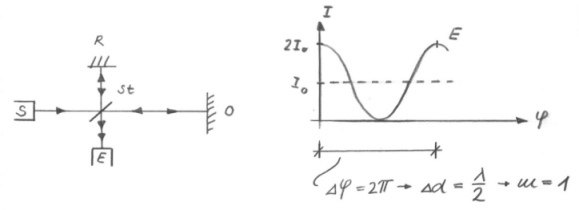
Bei der Interferometrie werden die gleichen Überlegungen angestellt wie bei der Phasen-Laufzeitmessung. Der Unterschied jedoch ist, dass hier die Wellenlänge des Trägersignals verwendet wird, die etwa um den Faktor 10⁶ kleiner ist als bei üblicherweise verwendeten Modulationsfrquenzen. Dies hat auch eine andere Betrachtungsweise zur Folge.

Die Interferometrie kann auf die Tatsache zurückgeführt werden, dass das Interferenzmuster zweier verschiedenphasiger Wellen als Längenmassstab benützt werden kann.

Um zwischen dem ständig ausgesandten Signal und dem Referenzsignal die notwendige Kohärenz zu gewährleisten, wird die gleiche Signalquelle verwendet. Ein Teil des Signals wird zum Objekt gesendet und dort reflektiert. Das zurückkommende Signal wird mit dem anderen Teil des Signals verglichen, welches seinerseits eine bekannte Referenzstrecke durchlaufen hat. Die relative Verschiebung der beiden Signale wird mit der durch die Wellenlänge gegebenen Auflösung nach folgender Beziehung [11] gemessen.

 (2-22)

Die Anzahl Wellenlängen m, die sich bei einer Verschiebung ergeben, kann deshalb gezählt werden, weil sich die Addition zweier Wellen in der Intensität folgendermassen ausdrückt [11]:

 (2-23)

wobei

 (2-24)

Die starke Verwandtschaft mit der Phasen-Laufzeitmessung wird hier besonders deutlich. Die Intensität ändert sich zwischen 2I₀ und 0, wenn sich die Phasenverschiebung zwischen 0 und p     bewegt. Aus diesem Zusammenhang heraus ergibt sich die Gleichung (2-22).
 
Eindeutigkeit

nach [3][11]

Um absolut messen zu können, müssen auch bei diesem Verfahren mehrere verschiedene Frequenzen verwendet werden, da die Eindeutigkeit in gleicher Weise gegeben ist wie bei der Phasen-Laufzeitmessung. Dies schränkt die Skalierbarkeit entschieden ein. Sie liegt im mm-Bereich [3]. Eine Verbesserung wird erreicht, wenn zwei Wellenlängen benützt werden. Es lässt sich daraus eine neue, gedachte Wellenlänge berechnen, mit der eine grössere Distanz eindeutig gemessen werden kann.

Für zwei unterschiedliche Wellenlängen l₁ und l₂ gilt für die gleiche Distanz d folgendes:

 (2-25)  (2-26)

Haben die Anzahl Wellenlängen m₁ und m₂ ein gemeinsames Vielfaches, so sind die beiden Wellen gleichphasig. Sie bilden eine neue, gedachte Wellenlänge. Durch Subtraktion der obigen Gleichungen erhält man eine neue Beziehung für die Distanz.

 (2-27)

Verglichen mit der Gleichung (2-22) wird der Ausdruck für die gedachte Wellenlänge ersichtlich, mit der nun eine längere Distanz eindeutiger gemessen werden kann als mit beiden einzelnen Wellenlängen alleine. Sie werden so gewählt, dass m₁-m₂=1 ergibt. Dadurch wird das Resultat unmissverständlich.
 
Auflösung / Genauigkeit