กลไกเบรกดาวน์ของ Townsend

ตามทฤษฏีกลไกการเบรกดาวน์ของ Townsend (Townsend breakdown mechanisms) เบรกดาวน์ ในก๊าซนั้นเกิดขึ้นจากจำนวนอิเล็กตรอนที่เพิ่มขึ้นเป็นลำดับต่อเนื่องใน gab ระหว่างอิเล็กโทรด และเชื่อว่ากระบวนการเพิ่มทวีคูณของอิเล็กตรอนเกิดจาก Ionization กระบวนการขั้นต้น (primary or ? process) และ Ionization กระบวนการขั้นสอง (secondary process) ประกอบด้วย Ionization โดยไอออนบวกชนโมเลกุลของก๊าซ (?-process) แต่กระบวนการนี้ไม่มีความหมายในการทำให้เกิดเบรกดาวน์ กระบวนการขั้นสองที่มีความสำคัญต่อกลไกเบรกดาวน์คือกระบวนการ ? (?-process) อันเป็นกระบวนการที่เพิ่มทวีคูณของอิเล็กตรอนปล่อยหลุดจากแคโทด

     Townsend ได้ทำการศึกษาการเปลี่ยนแปลงของกระแสระหว่าง electrode แบบระนาบวางขนานกัน ดังรูป

รูปแสดงวงจรศึกษาทดลองของ Townsend

                อุปกรณ์การทดลองประกอบด้วย

- แผ่น electrode วางขนานกันมีระยะห่างเป็น X= d ภายในบรรจุก๊าซบริสุทธิ์ด้วยความดัน P

- Ampere meter และ Current  Limiting Resistor

- แหล่งจ่ายไฟฟ้ากระแสตรงแรงสูงที่ปรับแรงดันได้

การทดลอง
เมื่อทำการเพิ่มแรงดัน Vs ซึ่งตกคร่อม electrode ทั้งสองจะทำให้เกิดสนามไฟฟ้า E เราสมมติให้จำนวน electron เกิดขึ้นแรกเริ่มที่ขั้วลบ เนื่องจากการส่องแสง Ultraviolet ไปยัง Cathode และขณะนั้นจะมีกระแสเริ่มต้น ทำให้ electron เคลื่อนจากขั้วลบ ไปยังขั้วบวกและเกิดการชนกับมวลของก๊าซทำให้ electron เพิ่มขึ้น ซึ่งจะทำให้กระแสเฉลี่ยเพิ่มขึ้นตามเป็นเหตุให้เกิดการเบรกดาวน์ในที่สุดทั้งนี้จะขึ้นอยู่กับการสะสมพลังงานของ electron ค่าพลังงานสะสมนี้ขึ้นอยู่กับ E/P เมื่อ                     E เป็นสนามไฟฟ้า
P เป็นความดันของก๊าซ
ค่าพลังงานสะสมจะมีค่าคงที่เมื่อ E และ P มีค่าคงที่ จากการทดลองของ Townsend พบว่า
-กระแสในช่องว่างตอนแรก เริ่มจะเพิ่มขึ้นเป็นสัดส่วนกับศักย์ดาไฟฟ้า VB เนื่องจากว่า electron ที่ถูกปล่อยออกจาก Cathode เคลื่อนผ่านก๊าซด้วยความเร็วที่ขึ้นอยู่กับ VB
-เมื่อทำการเพิ่มศักย์ดาไฟฟ้าให้สูงขึ้นจนเกือบมีค่าคงที่เท่ากับ Io กระแส Io นี้ขึ้นอยู่กับความเข้มของการแผ่รังสี Ultraviolet
-ถ้าเพิ่มระดับความเข้มข้นของแสงมากขึ้นอีกระดับของกระแสจะเพิ่มขึ้นและคงที่เป็น Io ' ดังรูป

 

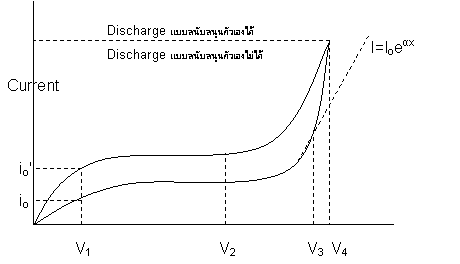
รูปแสดงความสัมพันธ์ระหว่างศักย์ดาไฟฟ้า   VB กับกระแสก่อนเกิดการเบรกดาวน์

-  เมื่อทำการเพิ่ม VB ขึ้นอีกเป็น V1 และ   V2     กระแสก็ยังคงมีค่าคงที่
-  ทำการเพิ่ม VB ขึ้นอีกจนถึง V3 กระแสก็จะเริ่มเพิ่มขึ้นอย่างรวดเร็ว
-  ทำการเพิ่ม VB ขึ้นอีกกระแสจะเพิ่มขึ้นอย่างรวดเร็วและเมื่อทำการเพิ่ม VB    ขึ้นอีกจนถึง V4 กระแสก็จะเพิ่มขึ้นอย่างรวดเร็วมากจนกระทั่งเกิดเบรกดาวน์


Townsend ได้อธิบายว่าเหตุเกิดจาก electron เกิดจากการไอออไนเซชั่นของก๊าซที่เกิดจากการชนกันของ electron จึงเป็นเหตุให้กระแสเพิ่มขึ้น เป็นแบบ Exponential ซึ่งช่วงนี้จะอยู่ในขบวนการของ alpha (Process)
แต่หลังจากที่ทำการเพิ่มศักย์ดาไฟฟ้ามากกว่า V3 กระแสจะเพิ่มขึ้นมากกว่าแบบ Exponential จนเบรกดาวน์ที่ V3
การเพิ่มขึ้นของกระแสในช่วงหลังนี้เกิดจากขบวนการ gramma (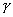 Process) ซึ่งขบวนการนี้เกิดขึ้นนอกเหนือจากการชนกันของ electron
ที่จุดเบรกดาวน์ V3 นี้ ศักย์ดาไฟฟ้าจะยังคงไม่เปลี่ยนแปลงแม้ว่าเราเปลี่ยนแปลงความเข้มของแสง Ultraviolet แต่ที่จุด V3 นี้จะเปลี่ยนไปได้ถ้ามี Space charge มาทำให้สนามไฟฟ้าเปลี่ยนไป
การเบรกดาวน์ของ Gap ที่ก๊าชความดันต่ำและแคบนั้น ศักย์ดาไฟฟ้าเบรกดาวน์ของ Townsend ที่ได้จากการทดลองและทางทฤษฎีมีค่าใกล้เคียงกัน จาก Graph รูปที่ 1.1 เป็นการเบรกดาวน์ของก๊าช ซึ่งเกิดขึ้น 3 ระยะคือ
 




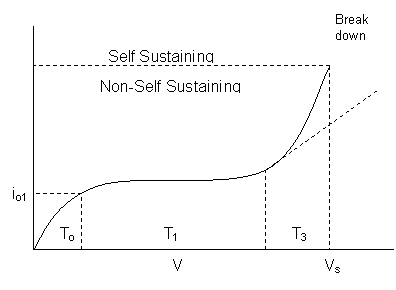
รูปที่ 1.1 graph แสดงการเบรกดาวน์ของก๊าช ระยะเริ่มต้น, ระยะปานกลาง และระยะสุดท้าย

1. ที่ระยะเริ่มต้น (To) จะเห็นว่ากระแสเพิ่มขึ้นอย่างช้าๆ เพราะว่าเกิดกระแสรั่วไหล

2. ที่ระยะปานกลาง (T1) กระแสที่ไหลค่อนข้างคงที่ เพราะว่าเกิดขบวนการ Ionization กับขบวนการรวมตัวของ electron (T2) สมดุลกัน

3. ที่ระยะสุดท้าย กระแสจะไหลอย่างรวดเร็วและมากมาย และในที่สุดก็จะเกิดการเบรกดาวน์ อย่างสมบูรณ์ (Completely Breakdown)

เพื่อให้เข้าใจขบวนการ Breakdown ของ Townsend ระยะ T1 และ T2 (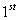 และ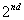) Coefficient Townsend mechanism เราจะอธิบายโดยใช้สมการ
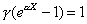                                                                                          (1.1)
หรือเขียนใหม่เป็น
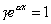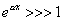                                   เทอม                                      (1.2)

จากความสัมพันธ์ของ  และ E/P สามารถเขียนเป็นสมการได้เป็น

                                                                                           (1.3)

                                                                                                  (1.4)

                และ Gradient E มีค่า
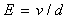                                                                                                (1.5)  

                                                               
สมการที่ 1.5 นี้ ใช้ในกรณีที่สนามไฟฟ้าเป็นแบบสม่ำเสมอมีศักย์ดาไฟฟ้า V มีระยะช่องว่าง d 
ทำการแทนค่า E จากสมการที่ (1.5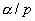) และ  และ 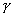 จาก สมการที่ (1.2) และ ลงในสมการที่ (1.3) และ (1.4)

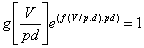                                                                       (1.6)

               จากสมการที่ (1.6) เขียนใหม่
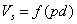                                                                                             (1.7)

               จากสมการ (1.7) แสดงถึง ศักย์ดาไฟฟ้าเบรกดาวน์เป็น Function ของความดัน p และระยะช่องว่าง d สมการนี้เราเรียกว่า (Paschen’s law)

 

Copyright ©2005 Thana Kaewtapee