CELLULAR
por Olmo del Corral (olmobrutall@hotmail.com)

Este es otro gran mapa (o grupo de mapas) dentro de las texturas procedurales, la invención del algoritmo pertenece, creo, a Steven Worley. En su página se pueden encontrar buenos ejemplos e imágenes, aunque anda un poco escaso de código ;(. Hay otra página (pagina 2) con excelentes imágenes echas con este algoritmo, aunque no explican como. Es un mapa muy útil en todas las texturas que tengan apariencia de células, teselas, escamas... y en general cualquier textura en la que se reconozca un patrón de elementos individuales unos pegador a otros que se repiten.

El algoritmo es en síntesis sencillo pero luego veremos que tiene muchas posibilidades y variaciones, y alguna que otra complicación. Podríamos decir que el algoritmo tiene 4 fases, vamos a anticiparlas:

1.- Distribución aleatoria de puntos: Se marcan las coordenadas de los píxels donde consideramos que hay un punto, cada uno de estos puntos será el pseudo-centro de nuestras células o teselas.

2.- Cálculo de distancias: Para cada pixel de nuestro mapa, se calcula la distancia a cada punto.

3.- Selección de las distancias menores: Según nuestro procesador y nuestra ambición, seleccionaremos la distancia del punto más cercano, o los dos, tres o cuatro más cercanos.

4.- Cálculo de valores finales con estas distancias: El mapa cellular permite 'jugar' con los 3 ó 4 valores de las distancias menores para conseguir curiosos efectos.

Distribución aleatoria de puntos:
En este punto nos encontraremos dos problemas: El primero es que, como hemos dicho, a priori, una textura procedural es infinita, eso quiere decir que necesitamos las coordenadas aleatorias de infinitos puntos en un plano infinito... ¿dónde metemos eso?. Una vez más, como siempre que aparece la palabra 'aleatorio', haremos uso de la función IntNoise.

La segunda es que, bien, ahora sabemos donde están estos infinitos puntos, pero... ¿voy a tener que calcular infinitas distancias (raíz cuadrada de suma de cuadrados de coordenadas) para cada pixel?. Teóricamente si, pero nos permitiremos hacer cierto truco en este aspecto, el truco consiste en encerrar cada punto en una casilla, de tal manera que haya un y solo un punto en cada casilla. Esto debería producir un mapa de aspecto algo más regular, pues le hemos quitado grado de libertad a los puntos, pero lo cierto es que es inapreciable.

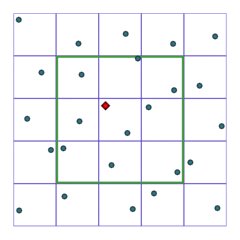Así quedarían los puntos, cada uno en su celda, el punto rojo indica el píxel que estamos calculando. De esta manera restringiríamos a 9 el número de puntos a los que tenemos que calcular la distancia: El punto que hay en la celda sobre la que estamos, y los puntos de las 8 celdas contiguas. Exactamente los puntos que hay dentro del rectángulo verde.

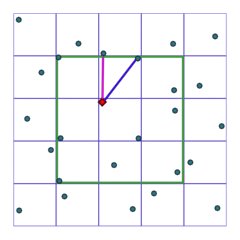Sin embargo en circunstancias extremas, si la surte nos juega una mala pasada y la distribución de los puntos en una zona de la textura es especialmente inconveniente, podría ocurrir que el punto mas cercano al pixel a estudiar no estuviera dentro del rectángulo verde de los 9 puntos a estudiar. Se aprecia en la figura que el segmento fucsia es mas corto que el morado, luego la distancia del punto mas cercano al pixel rojo, está fuera del cuadrado. Esto haría que nuestra simplificación no fuera 100% válida, y se produjeran en ciertos momentos errores en la textura.

La solución a este problema está en coartar aún mas la libertad de los puntos, haciendo que sólo puedan estar en un cuadrado interior a cada celda, centrado en el medio, y que diste aproximadamente 0.17157* de la pared de la celda... siendo 1 el tamaño de la celda entera. Esta solución es provisional, pues si bien garantiza que el punto más cercano estará en el gran rectángulo verde, no garantiza que pase lo mismo con el segundo o el tercero más cercano, sin embargo, para conseguir esto habria que coartar aún más los puntos, siendo, entonces ya si, apreciable la uniformidad de la textura. Además, ahora si es realmente improbable que ocurra el error con el segundo o tercer punto más cercano. Por estas dos razones no restringiremos aún más a los puntos. * Valor conseguido con cálculos de geometría

El código correspondiente a esta parte sería por tanto:

 float Cellular(float x,float y,int width,int tam_cas, int seed){
        double primero=2*tam_cas, segundo=2*tam_cas,tercero=2*tam_cas,dist_aux;   // No es de esta parte!
        int casilla_pto;                           // casilla de uno de los 9 puntos que se comparan
        double xpunto, ypunto;                     // coordenadas de los puntos de las 9 casillas
        int n_casillas=int(width/tam_cas)+1;       // para el famoso const del intnoise, igual que en Perlin
        int casillax=int(x/tam_cas);               // indice x de la casilla sobre la que está el pixel
        int casillay=int(y/tam_cas);               // idem y
        int casilla=n_casillas*casillay+casillax;  // indice final de la biyeccion de R^2 a R (idem perlin)
     for (int j=-1;j<2;j++){                       // para las 9 casillas...
       for (int i=-1;i<2;i++){                     //   
        casilla_pto=casilla+i+j*n_casillas;        // calculo de la casilla a estudiar con posición relativa
        xpunto=(casillax+i)*tam_cas+IntNoise(casilla_pto+seed)*tam_cas;    //calculo coordenadas de los
        ypunto=(casillay+j)*tam_cas+IntNoise(casilla_pto+10+seed)*tam_cas; // puntos aleatorios de las celdas
                                                                           // 9 contiguas
        ..... (continúa)       

Distribución aleatoria de puntos:
Es interesante saber que no hay una sola manera de calcular la distancia entre dos puntos, en el espacio euclidio se hace con el teorema de Pitágoras, pero en otros espacios podríamos definir la distancia de una manera distinta. De la definición de la función distancia dependerá, obviamente, el aspecto de la textura:

dist_aux=sqrt((x-xpunto)*(x-xpunto)+(y-ypunto)*(y-ypunto)); //Distancia Euclidea
dist_aux=abs(x-xpunto)+abs(y-ypunto);                       //Distancia Manhattan
dist_aux=max(abs(x-xpunto),abs(y-ypunto));                  //Distancia Cuadrada

Así varían los mapas dependiendo de la distancia elegida, se puede apreciar que Manhattan y Cuadrada son similares con distinta orientación. Animo a experimentar con otras definiciones de distancia!

Euclidea	Manhattan	Cuadrada

Selección de las distancias menores:

El algoritmo de selección de las distancias menores es sencillo, así que no me detendré en él. Éste toma las 3 distancias menores.

if (primero>dist_aux){ tercero=segundo; segundo=primero; primero=dist_aux; } else { if (segundo>dist_aux) { tercero= segundo; segundo=dist_aux; } else { if (tercero>dist_aux) {tercero=dist_aux;}} }

Cálculo de valores finales con estas distancias:
Ésta parte es probablemente la que más juego da de las 4. Dependiendo de que fórmula que utilicemos para conseguir el valor final a partir de los valores primero (P), segundo (S), y tercero (T) y un factor de corrección si fuera necesario (tam) podemos conseguir una gran variedad de efectos. He aquí algunos de ellos, primero en su versión con la distancia Euclidea, y después con la distancia Manhattan. (La distancia cuadrada no la he incluido pues es similar a la Manhattan).

255*P/tam	255*S/tam	255*T/tam	255*2*P/(S+T)
255*P/S	255*(S-P)/tam	255*(T-P)/tam	255*(T-S)/tam

Variaciones finales con distancia Manhattan

255*P/(2*tam)	255*S/(2*tam)	255*T/(2*tam)	255*2*P/(S+T)
255*P/S	255*(S-P)/(2*tam)	255*(T-P)/(2*tam)	255*(T-S)/(2*tam)

 

 

float Cellular(float x,float y,int width,int tam_cas, int seed){
          double primero=2*tam_cas, segundo=2*tam_cas,tercero=2*tam_cas,dist_aux;
          int casilla_pto;
          double xpunto, ypunto;
          int n_casillas=int(width/tam_cas)+1;
          int casillax=int(x/tam_cas);
          int casillay=int(y/tam_cas);
          int casilla=n_casillas*casillay+casillax;
       for (int j=-1;j<2;j++){
         for (int i=-1;i<2;i++){
          casilla_pto=casilla+i+j*n_casillas;
          xpunto=(casillax+i)*tam_cas+IntNoise(casilla_pto+seed)*tam_cas;
          ypunto=(casillay+j)*tam_cas+IntNoise(casilla_pto+10+seed)*tam_cas;
          dist_aux=sqrt((x-xpunto)*(x-xpunto)+(y-ypunto)*(y-ypunto));
          if (primero>dist_aux){
                tercero=segundo;
                segundo=primero;
                primero=dist_aux;
          }else {
                if (segundo>dist_aux) {
                                tercero= segundo;
                                segundo=dist_aux;
                                } else {
                                        if (tercero>dist_aux)
                                        {tercero=dist_aux;}}
          }
      }}
          return 256*2*primero/(segundo+tercero);
              }

ANTERIOR

INDICE

SIGUIENTE