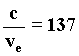When we calculate the velocity of an electron moving in the orbit through the value ra of 97) and apply the value ve in the ratio of the formula 95) we obtain. 99)
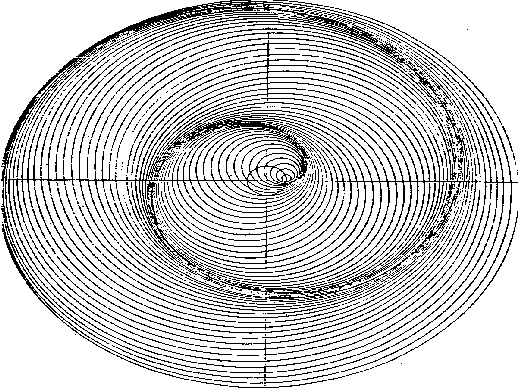
The physical meaning of the formula derives from the ratio of the velocity c of the wavefronts moving in the orbit and the velocity ve of the wave source-electron in the same orbit. We must remember that we are referring to those wavefronts moving along the ideal tube whose axis is the orbit on which the closed path of the electron-wave source lies. Figure 95 shows that "137" wavefronts of wavelength le move in the orbit in a resonance state, and that for each revolution made by the wave source the wavefronts coming from it make "137" revolutions. But this does not correspond to reality yet, since our description of the wave source-electron is not relativistic yet. When we apply relativity and the resonance law to the wave source-electron circulating in the orbit with velocity ve the relativistic Doppler wavelength le1 of the waves preceding the electron, which is shorter than le, is 138 times greater than the orbit of the radius ra. Moreover, when we take into account the waves propagating in the same orbit (in the same ideal tube) but moving in a direction opposite to the electronís motion, we see that with the same velocity as the wave source-electron, the opposite relativistic Doppler effect increases the wavelenght le2 so that it is 136 times greater than the orbit of the radius ra. The two wave trains travel at the same velocity c along the same path in a direction opposite to each other. If both wave trains are allowed to travel in resonance condition in the same orbit together with the wave source-electron, a wave variation appears moving in the orbit in the same direction as the electron. This is a sort of indipendent wave with a wavelenght equal to the orbital lenght of radius ra composed of the sum of the elementary wavefronts belonging to the two wave sources whose mean is 137. All of that explains the physical and geometrical meaning of the resonance condition which up to now seemed to be dominated but not explained by the number identifying fine-structure constant. Only now, it has found a rational and entirely justified explanation in the Wave Field Theory, thanks to a relativistic description of the wave composed of a beat which results from the coexistence of Doppler waves coming from the wave source-electron moving in the orbit L in the atom of hydrogen. This is the wave Louis de Broglie associated with the electron in the Bohr atom. It is the same wave Schrodinger describes as physically possible in wave mechanics, but that quantum mechanics considers as a mathematical function of the ďprobabilityĒ of finding the electron somewhere in the atom, and "accidentally" identical to the mathematical handling of a real wave. In our purely wave description we overcome the concept of "complementarity" of a dual handling, whose intention is - by definition and method- to combine the corpuscolar appearance with the wave physical nature of the Bohr atom. Hence, with the wave field theory, we arrive at a causal interpretation of the emission in the atom and therefore at a plausible wave explanation of photoelectric effects. First of all, in order to do that, we must understand the difference between the graphic image of a wave source-electron moving in a resonance orbit, and the image of the same wave source-electron in any "nonresonant" orbit. You will wonder if it is orthodox to be guided by a simple geometrical picture of a mental experiment; some of you will say no. But we must not forget that we are trying to geometrize physics, and that space and time are the only entities supposed to exist in our theory. The representation of the nonresonant case is so suggestive and full of explanatory elements that the difference with the graphic representation of the resonant condition is immediately and unmistakably evident.
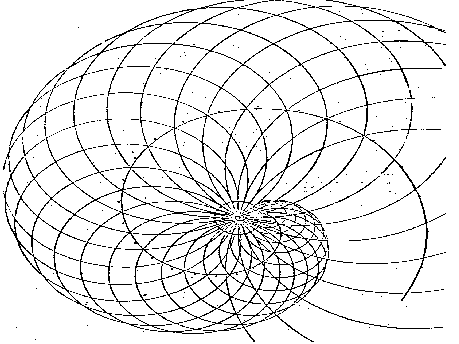
Fig.29 In the representation of the phenomenon where the electron moves in a non-resonant orbit, only the first condition is required:
The result is a wave which is a FREQUENCY MODULATION of the electronís elementary carrier wave.
And
this seems to be the real nature of the light emitted by the electron in
the passage from a resonance state to another. |