SEÇÃO I

» 1ª Unidade: História e Conceitos Básicos

• A Irracionalidade do Agente Racional: Risco e incerteza; psicologia, biologia evolutiva; o maximizador local e o global.

As diversas críticas recebidas pela Teoria dos Jogos, em sua forçosa simplificação da forma matemática do trato social, concentraram-se principalmente na concepção de agente racional adotada e a consequente construção artificial das situações estudadas. Alguns filósofos apontaram para insuficiência da visão econômica do mercado livre, onde as relações de troca sobressairiam a despeito da simpatia, do espírito de equipe e da confiança necessários ao convívio social (1). Outros atacaram a restrição da análise aos contextos competitivos que nem sempre surgem como tal no cotidiano, bem como as soluções insatisfatórias sugeridas aos jogadores na condição do Dilema dos Prisioneiros e outros modelos abordados (2). Houve ainda alguns, como Jürgen Habermas, que consideraram a adoção do ponto de vista das relações de troca nas esferas públicas - uma das aplicações do modelo de jogos - uma das fontes de patologias sociais que desequilibram a interação das sociedades modernas, que deveriam ser apoiadas de forma justa na solidariedade, no dinheiro e no poder administrativo (3).

Todas essas objeções filosóficas sucederam às observações feitas, na primeira hora, pelo economista francês Maurice F. Charles Allais, laureado com o Nobel de Economia de 1988. Allais combatia a excessiva formalização matemática que, na primeira metade do século XX, teve seus principais marcos teórico nas obras dos economistas italiano Vilfredo Pareto (1848-1923) e estadunidense Paul Anthony Samuelson, prêmio Nobel de 1970. Chamava atenção, sobretudo, para o problema da subjetividade, deixado de lado pela escola neoclássica em economia, que nos anos 1950, predominava nos Estados Unidos. Para Allais, as considerações sobre a cardinalidade das preferências individuais, isto é, a observação da intensidade da preferência de um sujeito por um determinado objeto, independente do seu ordenamento numa escala sequencial de utilidade, da maior para a menor, deveria ter um peso expressivo, a fim de explicar com mais naturalidade o comportamento racional diante do risco ou incerteza.

Aos adeptos do formalismo metodológico que dominou o início da Teoria dos Jogos, somente a relação ordinal de todas preferências e suas combinações possíveis para cada indivíduo tornaria possível a comparação e análise da utilidade entre pessoas de gostos e culturas diferentes (4). Contudo, os paradoxos apontados pelos experimentos de Allais indicaram que tal ordenamento não era suficiente para explicar a atitude dos agentes, ditos racionais, frente a opções de sorteio [vide exemplo deste autor em "A Estrutura do Jogo"]. A avaliação subjetiva das probabilidades entre duas loterias objetivamente semelhantes revelou a dificuldade de se manter a transitividade das preferências, um dos axiomas da teoria da utilidade adotada pelos teóricos dos jogos. Perdas e ganhos absolutos mostraram suas influências nas escolhas em arranjos diferentes que conduziam aos mesmos resultados. Em geral, quanto maior fosse o ganho visualizado, maior era a aversão ao risco, e, como de frente ao espelho, quanto maior a perda, maior a busca do risco.

Efeitos dos Defeitos

Daniel Kahneman, com a colaboração de Amos Tversky, analisou diversos resultados obtidos em cenários diferentes, onde as pessoas eram submetidas a escolhas como nas experiências de Allais, e pôde detectar os efeitos cuja existência reflete a maneira pela qual os agentes racionais deliberam antes de desempenharem uma linha de ação. Os fenômenos observados na reação de estudantes de universidades israelenses e dos Estados Unidos chocavam com alguns pilares da teoria da utilidade. Empiricamente, constatou-se que as pessoas superestimavam resultados que são considerados certos - o chamado efeito de certeza -, em face daqueles que para serem obtidos envolveriam o cálculo das probabilidades. Cerca de 82% de 72 estudantes entrevistados escolheram (Loteria I)...

1. ganhar $2.400 certos,

 B.

$2.500, com probabilidade de 33%;

$2.400, com probabilidade de 66% e

nada com probabilidade de 1%.

Contudo, ao se depararem com outra situação (Loteria II) entre

1. a chance de 33% de ganhar $2.500

2. $2.400 com probabilidade de 34%,

a maioria de 83% optou pelo sorteio "A" que era nove utiles acima da segunda loteria, violando o axioma da substituição, como advertira Allais. Pelo axioma da substituição, se a probabilidade de ganhar mais em "A" é preferida à de "B", deveria ser preservada a mesma preferência em outro quadro, onde a certeza de um ganho oferecido em "A" fosse igualmente menor que a chance de obter o mesmo resultado anterior, agora em "B" (5).

O efeito da certeza foi observado em perspectivas que não preocupavam os agentes com perdas ou resultados negativos. Os casos que envolviam prospectos negativos, por sua vez, apresentavam outro fator virtualmente invertido em comparação ao de certeza, chamado efeito de reflexão. Como em um espelho, as respostas oferecidas pelos entrevistados refletiam uma ordem inversa das preferências para perdas, em contraste com as preferências por ganhos. Assim, entre 95 estudantes, 20% preferiram a loteria (Loteria III) cujo prêmio era...

1. $4.000, com probabilidade de 80%,

2. $3.000 garantidos

1. perda de $4.000 a 80% de chance,

2. perder imediatamente $3.000.

Os ganhos positivos provocaram nos agentes aversão ao risco, enquanto os quadros de expectativas negativas estimulavam, ao contrário, a busca ao risco. Nessas ocasiões, os mesmos "equívocos" provocados pelo efeito de certeza foram notados em ambos os aspectos, positivo e negativo, com a busca pelo ganho seguro, mas de utilidade menor e preferência por resultados negativos incertos, embora de maior perspectiva, do que a perda absoluta. Por conseguinte, o efeito de reflexão eliminou a aversão pela incerteza nos sorteios negativos, como consequência paradoxal ao efeito de certeza, passando a incrementar a aversão por perdas e o desejo de ganhos imediatos (6).

A maneira pela qual os cenários eram montados, seja com loterias de resultados positivos ou negativos, gerou atribuições de valores diferentes pelos participantes aos sorteios. Isso ficou ainda mais evidente quando se detectou o efeito de isolação em arranjos feitos com resultados obtidos a partir de probabilidades equivalentes. Para facilitar a escolha, com frequência as pessoas deixavam de separar adequadamente os componentes semelhantes e distintos, nas situações propostas. Em decisões que tinham de ser tomadas em duas etapas sucessivas, como no seguinte exemplo (Loteria V - figura 1), onde havia a possibilidade de nada ganhar imediatamente e 25% de passar ao segundo estágio, no qual teria de escolher entre $4.000, com 80% de chance, ou obter $3.000 de uma vez, nas escolhas feitas antes do jogo começar, 78% preferiram a última opção - dois porcento a menos do que na Loteria III. Entretanto, quando defrontados com outra perspectiva, de ganhar $4.000 com 20% de probabilidade ou $3.000 com 25% (Loteria VI - figura 2), a primeira alternativa era selecionada por 65% dos entrevistados, apesar desta ser equivalente a primeira alternativa da situação anterior (Loteria V), já que 1/4 de 80% seria a taxa de 20% associada aos $4.000 daquela. De fato, os participantes interpretaram o jogo de dois estágios, como o da Figura 1, na perspectiva da formulação padrão da Loteria III e não a da Figura 2, devido o enfoque isolado da decisão tomada no segundo estágio da Loteria V (7).

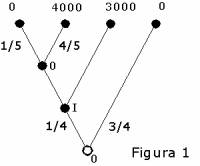
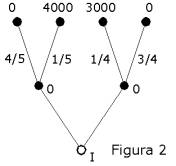
As deliberações feitas em mais de uma etapa levam em conta a correspondência entre as projeções sem risco e a arriscada, a despeito da mudança objetiva das respectivas probabilidades ou resultados, tendo em vista todo caminho a ser percorrido. Ou seja, a sequência de sorteios em estágio permitiria, na visão dos envolvidos, descartar as perdas dos valores oferecidos antes, em uma única perspectiva a partir do seu ponto de decisão, como na formulação sequencial da figura 1, ao invés de duas situações isoladas da figura 2, na qual os resultados estavam vinculados a probabilidades de ganho, separadamente. Tal modo de compreensão viola a hipótese de que a seleção de loterias deveria ser determinada pela probabilidade final dos resultados, recaíndo a escolha sempre pelo maior ganho provável. O isolamento das projeções indicou que a certeza contingente de ganhos fixos atrai as pessoas para este resultado, mesmo depois de uma sequência de movimentos na qual a sorte interviu, ao contrário do que acontece em loterias com opções separadas, mas com chances idênticas a de outro quadro que tenha sido posto à frente do agente, embora em moldura diferente.

Na Teoria das Perspectivas (Prospect Theory) que desenvolveram para explicar a maneira pela qual os indivíduos deliberam sob risco, Kahneman e Tversky atribuíram muitas das anomalias detectadas à fase de "edição" das perspectivas, quando muitas operações que transformam os resultados e probabilidades são feitas - a saber: ordenação (coding) dos ganhos e perdas; combinação das probabilidades de resultados idênticos reduzida a uma só probabilidade; separação dos componentes sem risco dos incertos e cancelamento dos elementos comuns de uma mesma oferta, em loterias com mais de um movimento. Tudo em função das projeções oferecidas. Neste instante, as ofertas são editadas de diversas maneiras, segundo o contexto em que surgem. Assim, pequenas diferenças são eliminadas e componentes comuns cancelados por simplificações, provocando as inconsistências observadas depois. Ganhos com probabilidades extremamente baixas são descartados, amiúde, na fase de edição, enquanto as chances muito altas tornam os resultados "certos".

Por outro lado, em um fenômeno atribuído a uma função de pesagem (weighting function), as pessoas preferem loterias que ofereçam altos valores com baixa probabilidade de ganhos, ao invés de valores pequenos e certos, como em $5.000 com 0,1% de chance, em lugar de $5 garantidos. Embora, aceitem pagar estes mesmo $5 a se arriscarem ao prejuízo de $5.000 com 0,1% de probabilidade. Além disso, a diferença entre pequenos montantes parece maior do que aquela variação de valores entre quantias maiores, como o incremento que é notado facilmente na passagem de 100 para 200 e quase ignorado na subida de 1100 para 1200 (8).

Essas distorções oriundas da fase de edição levam a simplificações que são orientadas pelo princípio de escolha da perspectiva de valor superior. Ao mostrar isso, a Teoria das Perspectivas passou a ser considerada a tentativa mais precisa de descrever o comportamento de agentes racionais em cenários de risco ou incerteza. Pôde-se, então, saber o porque das mudanças das preferências pessoais nessas circunstâncias precárias. Notou-se também que a experiência prévia de cada um para situações semelhantes influenciam fortemente o momento de tomada de decisão. Pequenas mudanças na forma de apresentação das alternativas perturbam as escolhas, ainda que os resultados finais se mantenham os mesmos. A condição psicológica dos agentes racionais, portanto, pôde ser incorporada pela Teoria dos Jogos como um de seus elementos cruciais, agora que seus conceitos assumiam caráter formal de trato matemático. A probabilidade subjetiva e a cardinalidade das preferências voltavam a merecer uma maior atenção por parte dos economistas e matemáticos, no instante de projetar os modelos de jogos que se seguiram a essas descobertas.

A Interpretação Cardinal de Harsanyi

A falta de consistência das preferências, empiricamente observadas, abalavam não só o aspecto preditivo do modelo de racionalidade econômica, mas descartavam a possibilidade da teoria ser considerada com algum valor normativo. Sobre esse ponto, John Harsanyi argumentou que, em algumas condições motivacionais específicas, era possível defender a validade normativa da teoria da utilidade de Von Neumann e Morgenstern.

Ninguém duvida da validade normativa da aritmética, apesar da maioria das crianças não poder resolver problemas aritméticos de qualquer complexidade sem treino especial (HARSANYI, J.C. "Normative Validity and Meaning of von Neumann-Morgenstern Utilities", p. 307).

Assim, o problema principal para sustentação da normatividade da funções de utilidade assentava na necessidade dos agentes racionais passarem a tomar atitudes orientadas adequadamente pelo resultado, ao invés de aterem-se exclusivamente à utilidade do processo. Nesta ótica, as escolhas devem ser feitas com base apenas na avaliação da possibilidade dos vários resultados disponíveis. Todo nervosismo do envolvimento com uma atmosfera estimulante de aposta, bem como outras experiências psicológicas deste tipo, deveria ser deixado fora do processo de deliberação. No entendimento de Harsanyi, as atitudes orientadas pelo resultado devem ser guiadas somente por suas utilidades resultantes que são assinaladas a cada loteria e por suas respectivas probabilidades (9).

Deste modo, os axiomas da teoria que garantiriam a monotonicidade (a loteria preferida será aquela que for a de maior ou igual probabilidade de fornecer a alternativa preferida) e a indiferença entre probabilidades equivalentes poderiam preencher os requisitos da racionalidade normativa, embora não fossem adequados para pessoas orientadas pela utilidade do processo (10). Nos termos de Harsanyi, pessoas orientadas pelo processo assumem uma atitude intrínseca de gostar ou não gostar da situação da aposta, dependendo da utilidade positiva ou negativa a ela associada, enquanto pessoas orientadas pelo resultado têm uma atitude instrumental em relação às probabilidades subjetivas vinculadas aos vários possíveis resultados, segundo o gosto pelos vários ganhos disponíveis (11).

Para poder lidar com esses casos, é preciso agora que a função de utilidade seja entendida como uma função cardinal e não só ordinal. Isto porque, a cardinalidade permitiria a comparação não só do nível de utilidade entre os indivíduos, mas também a utilidade de diferenças entre loterias para o próprio agente, o que facilitaria a observação das intensidades ou importâncias atribuídas por cada um a tais sorteios. Formalmente, alguém que prefira, por exemplo, A > B e C > D, quando defrontado às seguintes loterias:

L₁ = (A, 1/2; D, 1/2)
ou
L₂ = (B, 1/2; C, 1/2)

...preferirá a L₁ com mais intensidade do que L₂, caso prefira L'₂ = (A, 1/2; C, 1/2) mais do que L''₂ = (B, 1/2; D, 1/2), indicando a intensidade e importância dada pelo agente à relação A > B, quanto maior for a diferença entre A e B em comparação à existente entre C > D. Em outras palavras, qualquer loteria que "A" estivesse em jogo seria preferível sobre aquelas outras possíveis em que estivesse ausente. Assim, a utilidade cardinal aferida poderia conduzir, daqui à utilidade dos resultados de quem adotasse corretamente uma atitude instrumental frente aos riscos, na observação adequada dos valores em jogo, enquanto que a atitude intrínseca limitaria o alcance das escolhas das pessoas que gostassem ou não de apostas.

Dessa forma, Harsanyi chamou atenção para o fato de incluir uma interpretação cardinal dos pagamentos nas análises das escolhas sob incerteza, ao invés de uma concentração exclusiva com a relação ordinal dos ganhos. A despeito de economistas e matemáticos rigorosos atacarem a cardinalidade, influenciando até mesmo a base teórica empregada pelo filósofo canadense David Gauthier que em Morals by Agreement se ateve apenas à concepção ordinal dos ganhos e das preferências. A importância de observar os ganhos cardinais está na possibilidade de se estabelecer estratégias mistas apoiadas em valores contínuos de intensidade que podem variar em grau numa escala intervalar de resultados. O que não é viável quando se toma só a ordem de valores e a posição dos resultados numa escala de preferências que não leva em conta o peso de cada preferência, mas apenas que uma é preferível a outra em um elenco ordenado de resultados, não importando o quão um valor é mais preferido do que outro (12).

A Irracionalidade Humana e a Racionalidade Fora da Espécie

Uma postura pela interpretação normativa da racionalidade da teoria da utilidade, como a proposta por Harsanyi, deixa de lado críticas que poderiam ser feitas quanto ao caráter descritivo da teoria, pouco precisa ou inócua para seres vivos, que nem sempre agem de modo racional ou sequer possuem um aparato cognitivo desenvolvido para a realização desses cálculos todos. Os primeiros ancestrais humanos não desenvolveram uma habilidade específica para realização rápida dos cálculos exigidos na adoção dos seus efetivos interesses informados, posto que nunca teriam se defrontado com problemas que exigissem um método eficiente de escolha instintiva. Quem defende o valor normativo do modelo de jogos – tal qual Harsanyi - precisa argumentar então que, nas condições atuais da complicada vida em sociedade, o treinamento no uso de modelos matemáticos poderia "esclarecer substantivamente muitos problemas da ética" (13).

Certo é que a formalização matemática implica numa capacidade racional que excede a da maioria dos seres humanos, mesmo depois de solucionado o último Teorema de Fermat. Entretanto, isso não impede que organismos dos mais simples pudessem ser interpretados como "agentes" dotados de aptidão reativa suficiente para poderem seguir as estratégias analisadas pela Teoria dos Jogos. Claro que para os casos dos seres não humanos o conceito de racionalidade empregado sofreu profunda transformação, a ponto de permitir a concepção de uma racionalidade mínima e intencionalidade capaz de incluir até bactérias e vírus (14).

Para a Teoria dos Jogos, um jogador é considerado racional se está motivado a maximizar seu próprio ganho, ou seja sua utilidade, sendo ainda hábil para calcular os resultados estocásticos (probabilísticos) de cada ação. Quando biólogos evolucionistas contemporâneos passam a utilizar modelos retirados desta teoria, no intuito de explicar o comportamento de determinadas espécies, estão interpretando essa racionalidade instrumental, agora, como uma capacidade de reunir informação e reagir em conformidade a esta. Ou seja, uma habilidade computacional do trato da comunicação que pode ocorrer mesmo no processamento de informação realizado por seres vivos através de reação de meras substâncias químicas. Pombos, falcões, bactérias ou vírus presentes em modelos virtuais ou em experimentos reais de laboratórios estão aptos a tomarem parte de um Dilema dos Prisioneiros Iterado, que se repete por várias vezes, graças a sua capacidade computacional de trabalhar as informações de entrada e reagirem com uma resposta adequada (15).

Muitos biólogos, depois de John Maynard Smith ter estabelecido uma "teoria dos jogos dinâmicos evolucionários" (o marco é o livro Evolution and the Theory of Games de 1982), passaram a aplicar os novos recursos de análise matemática em pesquisas sobre linguagem, justiça (fairness) e direito de propriedade que até então ficavam restritos à especulação filosófica em suas diversas sub-áreas. Pela teoria dos jogos evolucionários, as escolhas das ações seriam determinadas não pelo agente racional clássico, mas por estratégias específicas, cujo sucesso implicava no número maior de descendentes na futura geração. A partir desta concepção, uma estratégia evolutivamente estável (EEE, ou ESS, do inglês evolutionarily stable strategy) seria aquela que pudesse gerar condições de equilíbrio. Nenhum indivíduo portador dessa estratégia conseguiria incrementar sua capacidade reprodutiva, se a trocasse por outra estratégia e nenhum mutante portador de estratégia rival diferente seria capaz de invadir a população na qual EEE prevalecesse (16).

Para uma estratégia ser considerada EEE, deve atender a duas condições quanto ao equilíbrio: seus resultados devem ser equivalentes aos pontos de equilíbrios estritos - ou seja, são as melhores respostas obtidas através de estratégias puras - e, por outra, a condição de estabilidade também deve ser satisfeita, isto é, as diferentes respostas às melhores estratégias dos outros são correspondentes as melhores respostas do agente (17). Por conseguinte, estendida a um grupo vivente, de acordo com Richard Dawkins, uma EEE é a estratégia inata adotada pela maioria da população que não pode ser superada por uma outra estratégia invasora (18). Da perspectiva evolutiva, não há necessidade de se considerar tais estratégias conscientes, basta as compreender como "programas de comportamento inconscientes estabelecidos pelos genes" (19). Uma concepção assim pode abranger desde o vírus Influenza e bactérias Escherichia coli até os seres humanos (Homo sapiens sapiens).

Desse modo, o sucesso da Teoria dos Jogos Evolucionários permitiu explicar o comportamento de insetos e vertebrados, sem apelar para uma hipótese de racionalidade forte, cujos testes de campo abalavam a tradicional teoria estática dos jogos. A partir do instrumental estruturado na teoria dos jogos original, a biologia evolutiva conseguiu analisar e prever as escolhas feitas por humanos dotados também desse tipo de racionalidade fraca que busca em primeiro lugar garantir a sobrevivência dos indivíduos e promover sua reprodução nas gerações futuras. As diferenças entre as espécies poderiam, a partir de então, ser discriminadas tendo em vista a diferenciação de estratégias adotadas por cada grupo de genes que compõem determinado organismo, variando desde os maximizadores irrestritos aos "altruístas" maximizadores restritos.

Maximizador Local e o Global

Durante os dois milênios e meio que constituem a história da filosofia, os filósofos se ocuparam em definir os seres humanos como seres racionais, divergindo aqui e ali sobre o grau e a categoria de raciocínio que este ente poderia exercer. Mas todos estavam de acordo que a racionalidade era algo que distinguia a espécie humana dos outros animais. Com a teoria dos jogos evolucionários essa distinção cai por terra, restando apenas o refinamento das estratégias como diferenciação entre agentes maximizadores irrestritos "egoístas" e aqueles capazes de restringir suas ações imediatas em função de um ganho maior no futuro. A irracionalidade humana passa a ser considerada um componente real a ser investigado, como nos outros seres vivos, que torna todos passíveis de erros sem que as fronteiras das espécies sejam uma barreira natural a definir quem é quem cognitivamente. Trata-se afinal de genes que disputam o direito de continuarem existindo e se replicando por maior período de tempo possível, abordo de "máquinas vivas". E para isso, fazem uso dos mais diversos tipos de estratégias.

Estratégias rotuladas como do "trapaceiro" ou do "rancoroso" - nos termos utilizados por Dawkins em O Gene Egoísta (1976) - podem alcançar estabilidade em meio a uma população de seres que usem a estratégia do "tolo". Imagine, como Dawkins fez, que os trapaceiros - seres que não cooperam nunca - invadam uma população tola, que coopera sempre, incondicionalmente. Qualquer que seja a quantidade de trapaceiros, desde que seja maior que um, irá prosperar e se multiplicar, explorando o trabalho dos tolos, até a exaustão destes, sem nada oferecer em troca. Tal estratégia será considerada evolucionariamente estavel ainda que leve a população de tolos à extinção, embora, em um território restrito, a morte do último tolo venha eliminar o próprio sustento dos trapaceiros, quando estes dominarem todo lugar, impedindo que outros seres portadores de outras estratégias entrem em cena. Motivo pelo qual se considera a estratégia do trapaceiro imune à invasão.

Diferente dos tolos, a estratégia "rancorosa", apesar de cooperar sempre que a outra parte coopera, é capaz de retaliar o adversário, caso este não retribua com um ato de cooperação, desertando. Em meio aos tolos, os rancorosos prosperam tanto como estes em razão da cooperação mútua entre eles, passando mesmo despercebidos por um observador externo. Contudo, ao contrário dos tolos, os rancorosos são robustos o suficiente para repelirem a invasão de trapaceiros, posto que reagem contra a deserção destes, impedindo que proliferem em seu meio. Num ambiente em que convivam as três estratégias citadas, os rancorosos conseguirão manter-se em número razoável, enquanto os trapaceiros levam os tolos à extinção. Apesar da baixa na quantidade inicial de indivíduos, em função da exploração inicial sofrida, os rancorosos continuariam multiplicando-se, graças a cooperação mantida entre si. No instante em que sobressaíssem tão somente trapaceiros e rancorosos, os primeiros passam a conhecer a decadência e o gosto amargo da ingratidão, ao passo que os segundos começam a recuperar suas perdas colaborando entre si e discriminando os trapaceiros. Deixados a sua própria sorte, os trapaceiros lutarão uns contra os outros até a morte ou, se possível, fugirão do local, que passa a ser dominado, afinal, pelos rancorosos (20).

Pela teoria dos jogos evolucionários, a caracterização do agente racional independe de sua configuração física ou ontológica. O que está em jogo entre os seres vivos, racionais ou não, é a capacidade de seguir uma regra, por em prática uma determinada estratégia que pode ter sido herdada ou adquirida pela experiência. Esta noção de agência aproxima-se muito da concepção dennettiana de postura intencional para "sistemas que modulam informações e buscam objetivos" (21). Quanto mais simples esses sistemas, mais próximos das macromoléculas orgânicas aptas à auto-replicação. Aumentando o grau de organização e complexidade, maiores são as chances desses sistemas intencionais poderem escolher adequadamente as melhores alternativas disponíveis.

Seres humanos, portanto, devido ao seu alto grau de complexidade orgânica, diferenciam-se de outros viventes por sua capacidade de antever acontecimentos futuros, com maior nitidez, ao invés de estarem presos apenas aos fenômenos presentes. Na definição conveniente do sociólogo norueguês Jon Elster, humanos podem ser considerados como máquinas maximizadoras globais prontas a usarem estratégias indiretas. Em outras palavras, são capazes de esperar por um momento mais favorável, no futuro, para tomarem decisões corretas, ao invés de optarem imediatamente por um resultado vantajoso momentâneo. Ao contrário das máquinas maximizadoras locais - os demais seres vivos -, os humanos não teriam de esperar por uma mutação genética aleatória para trocar de estratégia. Poderiam perfeitamente escolher entre um elenco variado de linhas de ação cultivadas por grupos sociais diversos no seio da espécie e armazenada em sua memória histórica, além de contar com aquelas embarcadas no seu código genético ao longo da evolução. Por conseguinte, uma característica marcante da "racionalidade" humana está no trato estratégico do cenário em que se encontra, povoado por seres semelhantes que também podem reagir em função da avaliação das expectativas de ação dos demais atores relevantes, também dotados de conhecimento comum. Ao passo que um comportamento tipicamente paramétrico - como das outras espécies - adotaria a postura do indivíduo como sendo um único agente apto a variar seu comportamento em um meio constante que, como tal, serve de parâmetro fixo para suas ações (22).

A teoria dos jogos evolucionários chamou atenção para alguns aspectos vitais da caracterização dos agentes racionais. Ao lado da teoria psicológica das perspectivas, desenvolvida por Kahneman e Tversky, traça um panorama realista da condição humana, ignorado historicamente pelos filósofos e economistas. Juntas, essas teorias alertaram, sobretudo, para o fato de que humanos, como qualquer ser vivo, estão irremediavelmente vinculados aos princípios biológicos fundamentais de sobrevivência e reprodução. Além disso, sustentou como válida a postura teórica de um individualismo metodológico que deve partir de suposições egoístas, devido às limitações biológicas e restrições de recursos naturais, para só depois explicar o comportamento "altruísta" e a cooperação em grupos sociais. Por conta disso, a união entre Biologia Evolutiva e o modelo de jogos trouxe um maior poder descritivo à teoria dos jogos original. O continente, antes habitado apenas por inúmeras variantes de Robinson Crusoé, tornou-se mais rico em diversidade de agentes racionais. O sentido de racionalidade ganhou, então uma versão mais precisa ao detectar as imperfeições psicológicas, cognitivas e morais dos sistemas intencionais. E a importância da aprendizagem ficou ainda mais clara para a espécie humana.

Notas
1. Veja HOLLIS, M. Trust Within Reason, cap. 8, p. 162 e MACINTYRE, A. C.Dependent Rational Animals, cap. 9, pp. 114-118.
2. Veja BLACKBURN, S. Ruling Passions, cap. 6, pp. 161-198.
3. Veja HABERMAS, J. "Concepções de Modernidade", in Constelação Pós-Nacional, p. 195.
4. Veja SAMUELSON, P. A. Fundamentos da Análise Econômica, p. 156.
5. Veja KAHNEMAN, D. & TVERSKY. A. "Prospect Theory", pp. 265 e 266.
6. Veja KAHNEMAN, D. & TVERSKY. A. Op. cit., pp. 268 e 269.
7. Veja KAHNEMAN, D. & TVERSKY. A. Idem, pp. 271 e 272.
8. Veja KAHNEMAN, D. & TVERSKY. A. ibidem, pp. 274 e 281.
9. Veja HARSANYI, J. C. "Normative Validity and Meaning of von Neumann-Morgenstern Utilities", p. 312.
10. Veja HARSANYI, J. C. Op.cit., idem.
11. Veja HARSANYI, J. C. Idem, p. 314.
12. Um exemplo de arbitragem - jogos com três jogadores, sendo o terceiro um mediador que não recebe nenhum ganho - adaptado de RAIFFA, H. El Arte y la Ciencia de la Negociación, III parte, cap. XVI, p. 240-242 esclarece como o peso que os indivíduos atribuem aos mesmos ganhos pode variar de intensidade entre eles. A negociação da divisão de $100 entre ricos e pobres revela o poder de barganha que permite ao mais poderoso arriscar mais do que o fraco na implementação de uma estratégia mista. A aversão ao risco conduz uma pessoa carente de bens primários a aceitar valores menores do que a média razoável de $50, quando se defrontam com um sorteio com a probabilidade de 0,5 de ganhar os $100 ou nada. Nestas circunstâncias, o pobre poderia contentar-se em receber $20 seguros, enquanto o rico arriscar-se-ia, possivelmente, à loteria, abrindo mão de $80 certos. Do ponto de vista de um mediador imparcial que fosse responsável pela divisão do prêmio entre os dois jogadores, seria injustificável racionalmente proceder a uma distribuição diferente de $50 para cada um, embora o ganho cardinal deste seja diferente individualmente. Isto é, para o pobre, metade de util, o que corresponderia na solução sem arbitragem ao ganho de $20. Já para o rico seria o mesmo que $80, devido à intensidade do desejo de possuir o bem em disputa. O pobre precisa mais do dinheiro, e por isso qualquer quantia seria bem vinda, mas o rico, que já tem muito, pode se dar ao luxo de arriscar a ganhar mais, sem comprometer sua psicologia.
13. HARSANYI, J. C. "Game and Decision Theoretic Models in Ethics", p. 671.
14. Neste sentido, muito contribuiu o trabalho do filósofo Daniel C. Dennett com textos sobre consciência que foram lançados a partir de Brainstorms (1978) e que culminam com Tipos de Mentes (1996).
15. Veja LEWIN, R. Complexidade, cap. 7, pp. 167-169.
16. Veja ROSS, D. "Game Theory", § 6.
17. Veja HAMMERSTEIN, P. & SELTEN, R. "Game Theory and Evolutionary Biology", pp. 939-940.
18. Veja DAWKINS, R. O Gene Egoísta, cap. 5, p. 94.
19. DAWKINS, R. Op. cit., cap. 10, p. 206.
20. Para os detalhes dessa bela fábula, veja DAWKINS, R. Idem, idem, pp. 206-208.
21. DENNETT, D. C. Tipos de Mentes, cap.1, p.31.
22. ELSTER, J. Ulises y las Sirenas, I, §§. 3 e 4, pp. 23-40.

BLACKBURN, S. Ruling Passions. – Oxford: Claredon Press, 1998.

DAWKINS, R. O Gene Egoísta; trad. Geraldo H. Florsheim. – Belo Horizonte: Itatiaia, 1979.

DENNETT, D. C. Tipos de Mentes; trad. Alexandre Tort. - São Paulo: Rocco, 1997.

ELSTER, J. Ulysses and the Sirens. - Cambridge: CUP, 1984. Ed. mexicana Ulises y las Sirenas; trad. Juan J. Utrilla. - México, D.F.: Fondo de Cultura Económica, 1989.

GAUTHIER, D. Morals by Agreement. - Oxford: Claredon Press, 1986.

HABERMAS, J. A Constelação Pós-Nacional; trad. Márcio Seligmann-Silva. - São Paulo: Littera Mundi, 2001.

HAMMERSTEIN, P. & SELTEN, R. "Game Theory and Evolutionary Biology", in AUMANN, R. & HART. S. Handbook of Game Theory with Economic Application, vol. 2, cap. 28, pp. 929-993. – Amsterdam: Elsevier Science, 1992.

HARSANYI, J. "Game and Decision Theoric Models in Ethics", in AUMANN, R & HART, S. Handbook of Game Theory with Economic Application, vol. 1, cap. 19. – Amsterdam: Elsevier Science, 1992. pp 669-707.

___________. "Normative Validity and Meaning of von Neumann-Morgenstern Utilities", in BINMORE, K., KIRMAN, A. & TANI, P. Frontiers of Games Theory, cap. 15. – Cambridge (Ma): MIT, 1993. pp. 307-320.

HOLLIS, M. Trust Within Reason. – Cambridge: CUP, 1998.

KAHNEMAN, D. & TVERSKY, A. "Prospect Theory". Econometrica, vol. 47, n° 2, pp 263-291, março. 1979.

LEWIN, R. Complexidade; trad. Marta R. Schmidt. - Rio de Janeiro: Rocco, 1994.

MACINTYRE, A. Dependent Rational Animals. – Chicago: Open Court, 1999.

RAIFFA, H. The Art and Science of Negotiation. - Cambridge (Ma): Harvard U. P. 1982. Ed. mexicana El Arte y la Ciencia de la Negociación; trad. Guillermo Cardenas. – México, D.F.: Fondo de Cultura Económica, 1996.

ROSS, D. "Game Theory", in Stanford Encyclopedia of Philosophy. Disponível na INTERNET via http://plato.stanford.edu/entries/game-theory/. Arquivo consultado em 2001.

SAMUELSON, P.A. Fundamentos da Análise Econômica; trad. Paulo de Almeida. - São Paulo: Abril Cultural, 1983.