Easements are used to provide a smoother transition from tangents to curves through the use of gradually increasing curvature. Although they may be based on different conic or spiral type curves, the most commonly used curve for highways and railroads is based on the clothoid spiral. Usually it is associated with banking or super elevation. However the clothoid does not fit every situation, thus the parabolic must be used to fill the gap. Two approximation types are presented in the NMRA Data Sheets; each with its own advantages.
NOTE: Since installation is thoroughly covered in NMRA Data Sheet D3c and several track work handbooks, it will not be covered here. Using a length of rail, the "bent stick" method provides the smoothest curve. Only those parameters which effect general curve considerations are covered. Most of the examples were developed to satisfy my own interests as an engineer for use on my layout with 36" minimum radius on the main and 24" on branch lines.
An idea of the parameters can help the understanding of the effects on offsets, overhang, their selection and usage. The discussion in the CURVE section illustrates some of the advantages. In order to select the best solution for each case, it is not necessary to understand all the mathematic developments presented to verify results. The conclusions should help as guidelines to better selection.
CLOTHOID OR SPIRAL EASEMENT
The clothoid has unique properties that make it highly desirable on both the prototype and models.
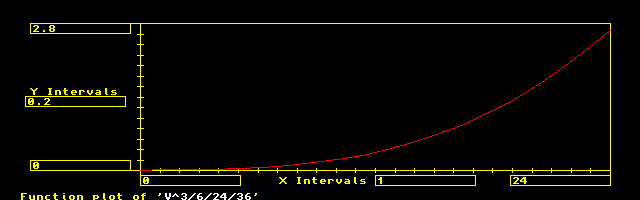
24" clothoid spiral easement for 36" R.
Even though the aspect ratio of height to width is just over twice for character legibility, the characteristics should be clear. At 8" the offset from tangent is only about .1" and the radius is 108".
The clothoid spiral easement has two basic equations that prompt its use. Where distances are measured from the tangent point along the curve, L is the total length and De is the distance to the point E in question. Using a rationalized curvature, where Ce equals zero at the tangent point and one at the curve point.
Ce = De / L
The curvature Ce increases linearly with De and at the mid point Ce = 1/2.
Re is the radius at De and Rc is the radius of the curve into which it feeds. The Radius equation is:
Re = 1 / Ce * Rc
Re = (L / De) * Rc
Regardless of length, the ratio of L / De determines Re. When De = 0, Re is infinite or a straight line. For Rc =36", at De = .1 L ; Re = 10 * Rc = 360". From 0 to L by .1 increments, the series for Re is:
Infinite or straight, 360, 180, 120, 90, 72, 60, 51.4 45, 40, 36
The second equation, involving the offset from the tangent extended, is used for layout.
Y = De^3 / (6 * Rc * L)
NOTE: For some unknown reason, the authors of the NMRA data sheet used X for the offset which is normally Y in engineering works. De^3 = De * De * De.
For normal modelling purposes only two values of De are of interest: the midpoint, where Dm = 1/2 L and the curve end where Dc = L. Using the "bent stick" method, the first locates the Ym offset and the 2 * Ym tangent offset from the curve, while the second locates the easement end point offset Yc. With a little juggling both can be simplified. Where Dm = 1/2 L , substitute for Dm:
Ym = Dm^3 / (6 * Rc * L) = (L / 2) ^3 / (6 * Rc * L) = L^3 / (8 * 6 * Rc * L)
Midpoint Ym = L^2 / (48 * Rc)
For a L = 24" and Rc = 36", it can almost be done in your head by .
Midpoint Ym = 24^2 / (48 * 36) = 24 * 24 / (48 * 36) = 2 * 2 / (4 * 3) = 1/3 = .333"
This offsets the tangent by 2Ym = .667" from the curve for a tangent distance of To = 36.667" from the curve center.
The curve end also simplifies similarly with Dc = L:
Yc = Dc^3 / (6 * Rc * L) = L^3 / (6 * Rc * L)
Curve end Yc = L^2 / (6 * Rc)
This simplifies the example to:
Curve end Yc = L^2 / (6* Rc) = 24 * 24 / (6 * 36) = 8 / 3 = 2.67"
To save computation note that the end value of Dc is twice the midpoint 0Dm and 2^3 = 8. Therefore the end value of Y is always 8 times the midpoint value.
Yc = 8 * Ym.
Since De is measured along the curve, the value of X along the tangent is not linear and is shorter than De. The solution results in the sum of a convergent series of terms and a lot of calculations. When De = 24", X = about 23.7" for about a 1.27% error. Using X along tangent line to layout Yc and Ym will lengthen easement slightly and not effect operation noticeably.
Although it is possible to connect tangents with sharp acute, diversion angles by overlaying easements, layout is very involved unless templates are used. To determine the minimum acute angle between two tangents with which two full easements can be used to connect them, the curve replacement angle must be found.

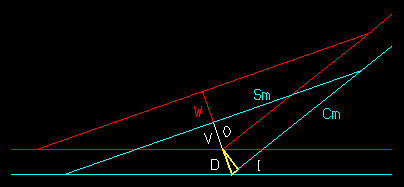
Divergence and central angles.
The easement is not shown for clarity. The yellow is the replaced curve section. While the angle to the left in the red, small bottom triangle is the tangent or slope at Yc. Since the legs of the two triangles are mutually perpendicular this angle equals the replaced arc central angle Ac which can be calculated..
At the Dm midpoint, the vertical distance from curve center to easement curve end Yc is found by subtracting Yc from the tangent line to center distance To = Rc + 2YM. The angle Ac is:
Ac = arcos ((To - Yc) / Rc) = arcos ((36.6667 - 2.6667) / 36) = arcos (34 / 36) = 19.19 º
A much simpler approximation is found by using 1/2 L and Rc
Ac = 180 * L / (2 * ¶ * Rc) = 180 * 12 / ¶ / 36 = 19.1 º
This would indicate that the minimum usable angle is about 38.4 º and for angles less than this, another type of easement is suggested.
For those who might be curious, at the midpoint Rm = 72" but the center is very close to 1/2 Dm or 6". To obtain T, 2 * Y must be added .
Y = 6^3 / (6 * 24 * 36) = .0417" and 2 * Y = .0833"
Am = arcos ((72.0833 - .3333) / 72) = arcos (71.75 / 72) = 4.776 º
This is 1/4 Ac at the half L value. Repeating at De = 1/4 L = 6", A = 1.194 or 1/4 of Am and 1/16 of Ac. So to a close approximation at :
Ae = (De / L) ^2 * Ac = (6 / 24)^2 * 19.19 = 1/16 * 19.19 = 1.199
Thus the angle varies as the square of the distance ratio.
PARABOLIC EASEMENT
For divergence angles less the minimum for the clothoid, the parabolic easement is recommended. The curve works very well, when constructed as described in the data sheet. One of the characteristics of a parabola is that light or other type waves parallel to the axis line B, impinging on the surface will be reflected to a focal point F. This is used extensively on flash or search lights and microwave or satellite dishes. To show that the curve is a parabola, the right side of drawing was constructed.
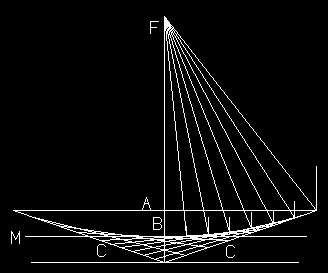
Characteristics of parabolic easement.
More important for easement use, is the fact that the minimum radius Rm occurs at the intersection of lines B and M. M bisects both C legs and B. By dividing C into an even number of segments and using the middle marks to draw M, it will be parallel to A. From the drawing, it can be seen that finer divisions yield a smoother curve.
Since the tangent intersection must be used to layout the divisions for the auxiliary construction lines, it is easier to calculate the leg distance C from the minimum radius Rm and the acute angle I between them. For Rm = 36 and I = 19.2 º, the half obtuse angle O is found first.
O = (180- I) / 2 = (180 - 19.2) / 2 = 160.8 / 2 = 80.4 º.
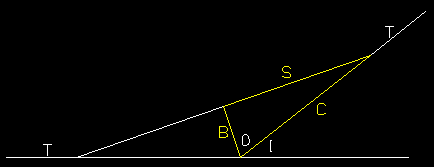
Yellow triangle to calculate C at tangent intersection.
To use it, the given equation is juggled and converted to a more usable form by defining S = 1/2 A.
Rm = A^2 \ 4B = (2S)^2 / 4B = 4S^2 / 4B = S^2 / B
Then:
B = C * cos O and S^2 = C^2 * sin^2 O.
Substituting:
Rm = C^2 * sin^2 O/ (C * cos O) = C * sin^2 O / cos O
Solving for C:
C = Rm * cos O / sin^2 O = 36 * cos 80.4 / sin^2 (80.4) = 36 * .167 / .972 = 6.175".
This seems like a very small distance, but it is a minimum. Any convenient longer length for C can be used to improve operation and appearance. Doubling C will yield an Rm = 72".
For the maximum of angle, I= 38.4 or double the above.
O = (180- I) / 2 = (180 - 38.4) / 2 = 141.6 / 2 = 70.8 º.
C = Rm * cos O / sin^2 O = 36 * cos 70.8 / sin^2 70.8 = 36 * .329/ .892 = 13.27"
C is slightly more than double, but still less than a desirable easement length. Using a 24" easement would yield an Rm of about 65.1".
Finding the radius Re at any point along the easement is a bit more complicated. Since the equation is derived from differential calculus with second order derivatives, it is the usual mess. X is measured parallel to S from the axis to the radius point. At the end of S, X= 12.53
Re = Rm * [1 + 4 * X^2 / Rm^2]^1.5
=36 * [1 + 4 * (12.53)^2 / (36)^2]^1.5 =
36 * [1 + 4 * .121]^1.5 = 36 * [1.484]^1.5 = 36 * 1.81 = 65.1"
NOTE:[]^1.5 = the 3/2 power or the square root of the quantity cubed.
Starting at the tangent track using X = 1 , .9, .8 .... .1, 0 times S, values are:
65.11, 59.16, 53.98, 49.56, 45.82, 42.74, 38.38, 37.05, 36.26, 36
For double the size with Rm = 72, C = 26.54 and S= 25.06:
Re = Rm * [1 + 4 * X^2 / Rm^2]^1.5 =36 * [1 + 4 * (25.06)^2 /(72)^2]^1.5 =
72 * [1 + 4 * .121]^1.5 = 72 * [1.484]^1.5 = 72 *1.81 = 130.3"
Finding the easement length is a bigger mess, but a good estimate can be found easily. Looking at the drawing below, it can be seen that the length is greater than S = 25.06 and and less than Cm + Sm = .5 C + .5 S = 13.27 + 12.58 = 25.85" (red lines). The actual value is close to 25.52 or about 2/3 the difference between them. This should help in selecting values for C to set easement length..
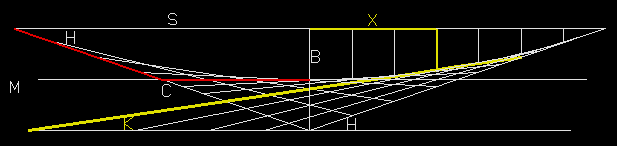
Relationships of easement length and slope angles at point X on easement.
Finding the offset angle from the tangent also uses the X and Rm values. The slope of the tangent at any point on the easement is X / Rm. Thus where X = S = 25.06 the slope angle K is:
K = arctan (X / Rm)= arctan (25.06 / 72) = 19.2 º
Starting at the tangent track using X = 1 , .9, .8 .... .1, 0 times S, angle values are:
19.20, 17.39, 15.56, 13.69, 11.80, 9.87, 7.93, 5.96, 3.98, 1.99, 0
The tangent track slope angle H is one half the offset angle I and equals 19.20 º. The angle J between the tangent and the slope is:
J = H - K = 19.20 º - K.
0, 1.81, 3.64, 5.51, 7.40, 9.33, 11.27, 13.24, 15.22, 17.21, 19.20
The rate of change is very near linear.
Note that only the divergence angle effects the characteristics of the easement. Modifying its size does not change the characteristics, due to the nature of a parabola. Even with the large radius near the tangent point, comparison to a clothoid reveals that the easement is not as gradual. However the overall effects are far superior to using circular curves as shown in the CURVES topic.
MULTIPLE TRACK CONSIDERATIONS
Multiple tracks add problems which are very rarely, if ever, addressed in articles. Proper clearance and increased track centers on curves require a gradual center distance increase throughout the easements. On clothoid easements, this will normally require a larger radius on the outside curve at all adjacent locations. but how much is the question. The ideal solutions are extremely complex; but, although not always obvious, practical ones are relatively easy.
The types of equipment you plan to run has a very strong bearing on selection of solutions and how drastic modifications may be. As shown in the section on curves, long rigid wheel bases on steam locos and particularly articulateds with boilers rigid on rear engine present the largest outside overhangs on inside curves. While rolling stock with long truck center distances present the greatest inside overhang on outer curves. These values must be determined before any decision for approach can be made.
The tangent offset 2Ym is used to determine double track easement compatibility. From above
Midpoint 2Ym = 2 * L^2 / (48 * Rc) = L^2 / (24 * Rc)
Consider two 24" clothoids connecting two, 2" center tangents, to a 36" and 38.5" concentric curves.
Inside 2Ym = 24^2 / (24 * 36) = 24 / 36 = .667
Outside 2Ym = 24^2 / (24 * 38.5) = 24 / 38.5 = .623
The tangent offset for the 36" is 2Ym = .667" for a total from curve center of 36.667. While for the 38.5", 2Ym = .623" for a total of 39.123. This would place the tangents at a center distance of 39.123 - 36.667 = 2.456" or .456" more than the 2" standard.
Among the several approaches to resolution, one is to gradually widen tangent center distance, when nearing curves. This may introduce an odd optical effect, if done on the outside.
Another approach is to adjust the outside easement to fit. The desired offset is 36.667 + 2 = 38.667". Then 2Ym is 38.667 - 38.5 = .167". The required length can be found by solving for L.
L^2 = 2Ym * 24 * Rc or L = square root (2Ym * 24 * Rc)
L = Square root (.167 * 24 * 38.5) = 12.42"
This is not much of an easement. Yet another approach is to lengthen the inside easement. Since the desired total offset for the inside easement is 39.123 - 2 = 37.123". The inside 2Ym = 37.123 - 36 = 1.123".
L = Square root (1.123 * 24 * 36) = 31.15"
This is 1.3 times as long as the 24" outside and about 3.6" longer along the tangent.

Relationships of dual 24" clothoid easements for 36" radius.
Inside 2Ym = 18^2 / (24 *24) = .5625
Outside 2Ym = 18^2 / (24 *27) = .5
Now tangent offset distances are 24.5625 and 27.5 for a difference of 2.875. This is .875 wider than the feeding tangent center distance.

Relationships of dual 18" clothoid easements for 24" radius.
Since the desired total offset for the inside easement is 27.5 - 2 = 25.5". The inside 2Ym = 25.5 - 24 = 1.5".
L = Square root (1.5 * 24 * 24) = 29.394"
This is about 1.633 times as long as the outside 18" easement and increase the length along the tangent by about 5.70". If space permits, this would reduce possibility of side swipes and yield excellent visual effect.
PARABOLIC
Parabolic easement curves require a different analysis which yields different results. For reasons seen below, the outside easement is selected first. Assume an Rm of 36", tangent track centers of 2" and a divergence angle I of 38.4 º and angle O = 70.8 º. Since the minimum radius occurs on the midpoint line M, this will be used instead of the A, B, C and S; thus all respective values will be exactly 1/2 the full easement value. First the distance between the two tangent intersections is found. In the small yellow triangle, the lower angle is O. So:
D = 2 / sin O = 2 / sin 70.8 = 2 / .944 = 2.12"
Relationships of dual parabolic easements at Rm mid point.
The recommended distance between track centers at Rm is about W = 2.625", requiring additional widening of 2.625 - 2.12 = .505". Using the minimum value found above for the outer easement, C = 13.27" and Cm = 6.64.
Bm = Cm * cos O = 6.64 * .329 = 2.18"
V = Bm - D = 2.18 - 2.12 = .06"
For the inside easement values would be:
Bm = V + W = 2.625 +.06 = 2.685"
Cm = Bm / cos O = 8.157" and C = 16.314"
Rm = C * sin^2 O / cos O = 16.314 * .892 / .329 = 44.24"
Possibly unexpected, this indicates that the inside Rm is larger than the outside and all factors of the easement are about 1.23 times larger.
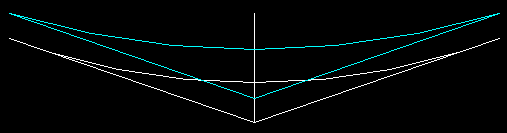
Relationships of dual parabolic easements.
The inside easement starts to separate from the tangent before the outside and the distance between the two steadily increases to the Rm midpoint. As with any easement longer is better.
Assuming a 24" easement with Cm = 12" and W = 2.25"
Rm = C * sin^2 O / cos O = 24 * .892 / .329 = 65.01"
Bm = Cm * cos O = 12 * .329 = 3.95"
V = Bm - D = 3.95 - 2.12 = 1.83"
For the inside easement values would be:
Bm = V + W = 1.83 + 2.25 = 4.08"
Cm = Bm / cos O = 12.41" and C = 24.82"
Rm = C * sin^2 O / cos O = 24.82 * .892 / .329 = 67.29"
Here the increases are not so drastic.
Understanding the principles above should lead to better selection of easements for each situation. Although they may appear complicated, they are easily constructed and well worth the effort in improved operation and visual effects.
BACK TO CURVES
BACK TO METHODS INDEX
BACK TO MEASURING INDEX
