The combination of curves and couplers plus car and loco geometry produces many problems, which may lead to derailments. At best even with 72" curves in HO, everything is hanging on the hairy edge. This is close to an extremely sharp 523' or about an 11 º curve on the prototype. Since most of us do not live in palaces, we are stuck with small radii.
Even with the recent expansion in variety of couplers, many problems have not been resolved. Compatibility and mounting still remain as problems, compounded by the other factors. Often in their zeal to produce realistic models, rolling stock manufacturers overlook the fact that they should also run well. Too frequently, insufficient thought goes into flexibility and the requirements of operation. This problem is left to the ingenuity of the modeller, who may not have the information to remedy it.
Graduating to the use of flex track, the problem of laying out curves arises. An understanding of the properties is very beneficial . First, the radius of all curves is measured at a point midway between running rails. Beyond that many factors enter into play.
Since it is very impractical to draw 1000' curves in the real world, surveying offset methods are used to layout curves. Referred to as a station , a 100' surveyor's chain is used to mark off distances along the curve. Except for very sharp curves; as a result, prototype railroads measure curves in degrees derived from stations.
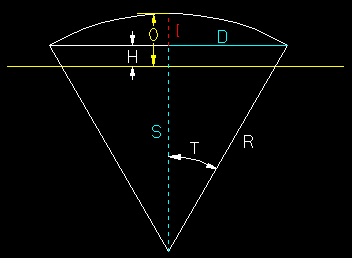
TheDEGREE OF CURVATURE is the angle A subtended by the chord or station C on the curve. The easiest way to convert is to bisect the angle (dotted line) and find the half angle T using the half station D, then multiply it by two.
A = 2 * T = 2 arcsin (50 / R)

Measurement of degree of curvature.
For a fairly sharp main line curve of 1,000', R = 137.8" in HO:
Conversely for 1 º curvature:
For model purposes the feet must be converted inches or centimeters by the scale factor. For HO 1 foot = about .13779 or .138. For an 18" R:
With radii in the mile range, the only practical layout method is with offsets using stations and a transit. However since this is not very practical in model use, it will not be covered. For those who are interested, some trackwork handbooks cover the subject.
In model layouts the usual method to layout curves is to draw arcs with string, yard sticks or trammels. The only basic requirement is that the radius is smooth throughout . Using a modified steel tape measure permits rapid and easy adjustments. However care must be taken to avoid sag in long distances.

Note: Adjust brightness and contrast for optimum viewing.
Tape measure with pivot, drawing hole and top readout .
On open benchwork temporary joists can be clamped in place to locate otherwise mid-air centers. An adjustable height tripod makes a handy center tool. Even with very accurate large scale trackplans, it is often difficult to locate centers. Often the best way is by trial, swinging small arcs from critical points or even the reverse. In most cases it is easier to rough in curves first to establish tangents later. For those using easements , it is wise to rough in arcs with offset radius to help locate tangents. Finer final adjustments can be made later, when laying out easements .
For those using cork roadbed and track with mid=rail nail holes, center lines may be drawn on sub-roadbed. One half piece of road bed is then lightly pinned and glued along the line. The second half is then butted against it and glued the same way. When set and nails are removed, the cork split establishes the center line for nailing track. Never nail ties too tightly, since this may bend them and throw rails out of gauge. For improved operation, by inserting a vee notched strip between nail head and tie as a spacer, the small clearance will permit some vertical motion or give. The major purpose of nails or spikes is to prevent horizontal motion.
Templates or gauges are great aids in spiking track at the rail. By pinning though a center hole they will hold track in place while spiking. Precut versions are invaluable to draw curve in locations where arcs can not be swung. Commercial gauges are available, but not in all scales or radii.
As exemplified by easements, radii need not be constant throughout a curve, but transitions must be gradual and smooth for both eye appeal and operation.
There are many factors effecting choice of radii, among which is the space allotted. A basic rule of thumb is to use the largest possible, whenever possible. Unfortunately very few models reveal their minimum radius, posing a great problem in selection. Many that will negotiate a radius will not perform well, due to geometry. Limitations in wheelbase, truck swing, overhang, and coupler mounting, all effect operation. A knowledge of these factors can help avoid the accumulation of "shelf models". It should be obvious that long pieces rolling stock do not fit well on short curves, but other factors may not be so obvious.
Although most have side play to compensate, particularly on steam locos, rigid wheel bases limit the minimum radius. Even the prototype was confronted with this problem, accounting for the multitude of flange-less or blind drivers. For minimum radius, in their designs, Baldwin not only included wheel base. but also diameter plus flange depth and contour. The attack angle was of prime consideration,

Greatly exaggerated rigid wheelbase on tight curve.
In addition to the possible binding, the attack angle of the end wheels can cause flange edge-rail contact, increasing the likelihood of picking flaws or riding over railhead. This could happen even with side play or blind drivers at higher speeds, due to centrifugal force or yawing.
Maximum truck pivot angle is often limited by steps, pilots, cylinders, and underbody details including coupler boxes. The amount required is increased by increasing truck pivot center distance and by decreasing radius. Coincidentally a good estimate of the angle for two truck equipment is found using the same method used to find the degree of curvature. The effects of axle end play are ignored.
C now becomes the truck pivot distance for cars. The yellow line is the truck center line which is tangent to the curve and perpendicular to the radius at that point. From geometry it can be shown that the upper right triangle is similar to the lower right triangle or that respective angles are equal. Therefore the truck angle, between yellow and blue lines, equals the curvature half angle T at the bottom.

Truck angle to car centerline.
Assuming an 8" truck pivot distance, with a half distance D of 4" (blue line) and an 18" R, this angle T is found by:
For locos D, or the equivalent P used later, is measured from the midpoint of the adjacent rigid wheel base to the truck pivot point. On the model the maximum available angle can be measured with a protractor or other device.
Divided into two categories, for multiple track curves, overhang becomes a problem because of possible side swiping. Worst cases are usually caused by long truck pivot distance cars on the inside of curves and articulated locos on the outside. Compared to tangent track center distances, this requires increasing the distance as radii decrease. Starting with a base of 13' = 1.79 º in HO, the PRR increased the distance on curves by 1" for every degree of curvature. Since an 18" R is 45 º, the addendum would be 45 scale inches = about .517 ", which in a practical sense too small even with the standard 2" = 14.5' tangent centers. Since they would be too small for practical application, model sideplay and flange to rail gauge tolerances are not scaled down proportionately.
NMRA Standard S-8 lists curve track centers and both inside and outside overhangs, but it is too general for every day use. Not every radius is listed, nor are specific types of cars or locos. In order to refine estimates for for your planning, measuring or computing values is recommended; to determine the minimums. Overhang values for specific rollingstock can help in planning clearances for associated structures on curves in tight spaces.
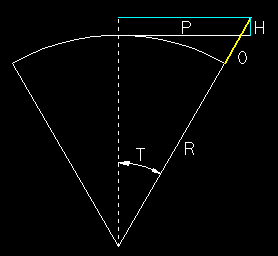
Although a little more involved, inside overhang is readily calculated as with other previous methods. The yellow line now represents the overhang and the problem is to find the distance along the dotted line from the curve center to the car center line. Among engineers versine or haversine tables are used, but most calculator or computer programs do not include these. Sticking to more common functions, calculation is relatively easy.
Along the dotted line, the overall process is to subtract the car center to the bottom triangle vertex, from the radius the add half the car width to the result. First find angle T as before using 8" pivot distance, D = 4" and an 18" R.
The vertex to car center distance S can be found several ways. First:
Without computing T, using the Pythagorean theorem:
Inside overhang.
The car center line overhang I:
The remaining value is the half width H of the car. Requiring the use of calipers, measurement should be over any extensions such as ladders, handrails, door runners or sills. Divide the value by 2 and add a little for side play. Shorter standard gauge prototype cars reach about 10'-6", while longer cars are frequently narrowed to 10' or less. Older clearances were narrower. Since actual side play varies and is very difficult to measure, usually I add about .02, but your guess may be better. The half width in HO is about .72, so for convenience .75 might be used. The total overhang O would be:
O = I + H = .45 + .75 = 1.22".
For R = 36":
O = I + H = .223 + .75 = .973".
Outside overhang is usually attributed to locos at the cab rear corners or pilots, but worst cases occur at smokebox fronts on articulated locos with the prototype method of mounting the boiler rigidly to the rear engine. The calculation is slightly different in that the half width of the obstruction point is added in first to locate the point. Rigid driver wheelbase locos are the easiest.
Outside overhang rigid driver wheelbase..
The blue line represents the half width H with addendum, while the yellow line is the overhang. Except for some very long Duplex types, where the cab may present a problem, H will normally be at the pilot. Since most locos have large amounts of side play to facilitate curving an addendum.03 or more might be considered in HO. Sample pilots measured about .7", so H = .73 is used. A medium sized loco measured about 3.25" from driver wheelbase center to pilot for P.
T = arctan (P / (H + R)) = arctan (3.25 / 18.73) = 9.84 º
O = P / sine T - R = 3.25 / sine 9.84 - 18 = 19 - 18 = 1"
For a long articulated steam locos with boiler fastened to rear engine, the greatest overhang would be at the smoke box front , where D might be about 5" with H equal to the smoke box radius or 4' = .55". But since in general these locos do not have the usual prototype centering devices on the front engine and they tend to yaw considerably, the addendum must be large. A guess might be .2" or more. This brings H up to .75".
T = arctan (P / (H + R)) = arctan (5 / 18.75) = 14.93 º
O = P / sine T - R = 5 / sine 14.93 - 18 = 19.4 - 18 = 1.4"
This is a hypothetical case, since the front engine is pivoted just forward of the rear and swing would be too small to negotiate the curve.
For R = 36":
T = arctan (P / (H + R)) = arctan (5 / 36.75) = 7.748 º
O = P / sine T - R = 5 / sine 7.748 - 36 = 37.089 - 36 = 1.089"
Diesels, cars and Rivarossi type articulateds with pivoted front and rear engines require more complex method since the pivot centerline has inside overhang which must be found first.
In this case, only the pivot center line to bottom vertex distance S is needed and H is added to it to establish the vortex to the yellow external line distance E. The H addendum is probably in the .03" range for most and .05" for articulateds. Rivarossi's Y-6b has an approximate C of 3.8", D of 1.9", P of 2.1" and H of .7 over running boards at smokebox front. With addendum H is .75"
Angle T = arcsin (D / R) = arcsine (1.9 / 18) = 6 º
S = 18 cos T = 17.9"
E = S + H = 17.9 + .75 = 18.65"

Complex overhang.
Now the outside vertex angle X is found from:
X = arctan (P / E) = arctan (2.1 / 18.65) = 6.42 º
The red offset is found by subtracting R from the total line length L from vertex to the smokebox runningboard corner.
L = P / sin X = 2.1 / sin 6.42 = 18.78"
O = L - R = 18.78 - 18 = .78"
Oddly this is less than that of the rigid driver wheel base locomotive. center line geometry makes the difference. As it will be seen later, this and couplers can cause problems.
Adjacent multiple curves require additional attention, as do any tracks on the outside of curves, straight or curved. To avoid side swiping, sufficient clearance must be maintained. For concentric curves, using the largest overhangs of equipment run on them, add the outside overhang of the loco to the inside overhang of the car. If the total is more than the minimum tangent track center distance (2" in HO), widening is necessary. Since the outside curve has a larger radius, recalculating the car inside overhang with this value may save some space. For multiple curves, starting at the inside, compute and refine each pair outward. For tangents outside curves, add half the standard distance to the outside overhang of the curve . With opposing curves, both outside overhangs must be totaled. EASEMENTS require special treatment, considered later.
COUPLER INFLUENCE
Couplers have always been the subject of many controversies, mostly on compatibility and operation. While comparisons and features will be covered under COUPLERS, only those that effect curves will be presented here. One exception is the consideration of gathering while attempting coupling on curves. Based on the overhang discussion above, the advice is simple. Unless curves are very large or equipment very short, if possible don't.
Coupler lengths, swings, springs, mounting and even knuckles, do play a major role in curve operation. Many derailments can be attributed to them directly or indirectly. Short of poor performance and design, the overall center line geometry is the largest culprit. It limits both curves and equipment length. But more than length must be considered.
On circular curves, worse case conditions are with a combination of cars at the extremes, in length such as a 40' express car coupled to an 85' passenger car. With body mounted couplers, an almost impossible condition exists on an 18" R. For 40' truck kingpin distance is 4.25" and pivot distance .5". For 85" kingpin is 8.125" and pivot is 1.5"
Note: All dimensions and angles were measured from scale drawings using XCAD 3000 professional on a Power PC Amiga 4000 to 6 digit decimal accuracy and rounded. Jagged lines are due to large magnifications and degradation from conversion to jpeg, but the computations are independent of display parameters. Since play in kingpin, axle ends and couplers is variable, it is not included for comparison.
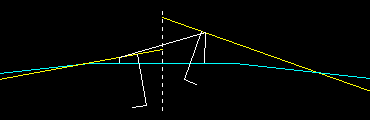
Enlarged offset at coupler pivots with coupler length .600" (KaDee #6).
The dashed line is at coupler faces, while the solid lines are the pivot offsets. The pivot connecting line is 2 x .600" = 1.200"
centerline angle = 29.57 º. Shank angles = 5.83 º & 35.40 º
Offsets: Track center-pivot = .066" & ..397". Difference = .331". Diaphragm = .424.
The centerline angle equals the difference between the two shank angles. The L shapes show corner post clearances.

Enlarged offset at coupler pivots with coupler length on 36" R w/ .481" (KaDee #5).
centerline angle = 14.52. Shank angles = 5.06 º & 19.58 º
Offsets: Track center-pivot = .033" & .2". Difference = .167". Diaphragm = .206 .
With a maximum shaft angle of about 20 º for for #5, another solution must be found. Possibly place 60' or 70' headend cars between. The other apparent method is to reduce coupler pivot to king pin distance. Talgo mounts have carried this to the extreme by reducing it to zero, with the trade off of shank truck pivoting torque. In some cases, spring centered drawbars may be used as a compromise.
BACK TO COUPLER AIDS
EASEMENTS EFFECTS
NOTE: Computing actual center line angles and offset values on easements is very complex, so only reasonable approximations will be used for illustration. Including multi-track applications , a more in depth discussion will be found at EASEMENT PROPERTIES.
Transition spirals or easements not only improve appearance, but greatly reduce the worst of offsets at tangent to curve transition. At this point one car is on the tangent, while the other is in the curve. Independent of its length the offset for the car on tangent at left is 0,

Transition from tangent to 36" R. with 85' passenger cars.
centerline angle = 9.56 º. Shank angles = 11.82 º & 27.39 º
Offsets: Easement-pivot = 0" & .2". Difference = .2". Diaphragm = .273".
A very large, abrupt change occurs in all angles and offset differences. The left shank angle is close to the maximum for a #5 box, while the right is beyond it. Even with a fairly large radius the coupler angles and offset difference are quite large. For the case where one car is on the tangent and the other is in an easement, the results are greatly improved.

Tangent end of 24" easement for 36" R with 85' passenger cars.
centerline angle = 1.40 º. Shank angles = 2.19 º & 3.59 º
Offsets: Easement-pivot = 0" & .037". Difference = .037". Diaphragm = .048".
Kingpin D, Y: Left = -10.106", 0" & -1.981", 0.. Right = 1.980", .0015" & 10.103", 1.989"

Left car kingpin at tangent end of 24" easement for 36" R with 85' passenger cars.
centerline angle = 7.94 º. Shank angles = 1.56 º & 9.50 º
Offsets: Easement-pivot = .046" & .116". Difference = .070". Diaphragm = .093".
Kingpin D, Y: Left = 0", 0" & 8.125", .106" . Right = 12.069", .339" & 20.101", 1.567"

Midpoint of 24" easement for 36" R with 85' passenger cars.
centerline angle = 9.36 º. Shank angles = .31 º & 9.67 º
Offsets: Easement-pivot = .065" & .127". Difference = .062". Diaphragm = .085".
Kingpin D, Y: Left = 1.897", .001" & 10.019", .194 . Right = 13.970", .526" & 21.938", 1.988"

Right kingpin at curve end of 24" easement for 36" R with 85' passenger cars.
centerline angle = 10.89 º. Shank angles =-.62 º & 10.27 º
Offsets: Easement-pivot = .083" & .142". Difference = .059". Diaphragm = .086".
Kingpin D, Y: Left = 4.054", .013" & 12.172", .348 . Right = 16.091", .804" & 24", 2.667"

Note:Adjust brightness and contrast for optimum viewing.
85' passenger cars on 36" R. .
centerline angle = 19.20 º. Shank angles = 9.60 º & 9.60 º 0
Offsets: Curve-pivot = .2" & .2". Difference = 0". Diaphragm = 0".
Conclusions: As the cars move through the easement, the centerline angle gradually increases from 0 º to 19.20 º with no abrupt changes. There is no gain, except the change is spread across the easement length.
The left shaft angle increases slightly in the first quarter , then decreases until it crosses the centerline in the third quarter, just beyond the midpoint.. It then increases rapidly to the value in the curve. The right shaft angle increases to a maximum in the third quarter, then drops to the value in the curve. When the shaft angles are on opposite sides of the center lines, the center angle is equal to the difference between them. When on the same side, it equals the sum. The maximum shank angles are reduced to about 39%.
Both coupler pivot offsets increase steadily to the curve maximum. Both pivot and diaphragm offset differences peak in the second quarter at about 34%.
Obviously both operation parameters and visual effects are greatly improved.
Although for hobby use easement lengths are arbitrarily chosen by space requirements, on the prototype, they are determined by the length of the super elevation ramp required and the amount of super elevation or curve banking is determined from train speed and degree of curvature. Higher speed and sharper radii require more super elevation, longer ramp gradient and thus longer easements. For model purposes, any easement is better than none and longer is better.
Wading through the deep waters above could help resolve many questions in equipment to curve relationships and selection. Since long wheel bases and geometry require larger radii, curves limit equipment selection. Widening track centers on curves depends on rolling stock over hang. Transition curves can help improve operation.
BACK TO EASEMENT PROPERTIES
BACK TO WEIGHT
BACK TO MEASURING INDEX
BACK TO TIPS ON TESTING
