Kapitel 7
Zyklus von 36 Jahren in Sonnenaktivität und Klima
Die Zyklen der Grossen Finger haben eine durchschnittliche Länge von 35,8 Jahren. Sie sind eng mit der Sonnenaktivität verknüpft. Sie fallen mit den Maxima und Minima des Gleissberg-Zyklus zusammen und ermöglichen deren langfristige Vorhersage [62, 63]. Wie wir noch sehen werden, bestimmen sie darüber hinaus die Länge des magnetischen Zyklus der Sonnenaktivität (Hale-Zyklus). Über den Gleissbergzyklus beeinflussen die Zyklen der Grossen Finger auch das Klima. Soweit es um Klimaschwankungen geht, ist eine Zykluslänge von 36 Jahren nicht neu. Schon Francis Bacon [102] wies auf einen 35- bis 40jährigen Zyklus in Holland hin, in dem feucht-kühle und warm-trockene Abschnitte aufeinander folgten. E. Brückner [7] entdeckte 1887 diesen Zyklus neu. Er zeigte, dass zahlreiche klimatische Phänomene, die in den verschiedensten Gebieten der Erde erscheinen, aber synchronisiert sind, einem Zyklus von 33 bis 37 Jahren folgen. Er vermutete schon damals einen Zusammenhang mit der Sonnenaktivität. H. W. Clough [11, 12] nahm diese Anregung auf und fand den Brückner-Zyklus nicht nur in zwölf verschiedenen meteorologischen Variablen, sondern auch in der Sonnenaktivität und insbesondere in Variationen der Länge des 11-jährigen Zyklus. D. V. Hoyt und K. H. Schatten [39] haben darauf hingewiesen, dass für die Realität des Brückner-Zyklus spreche, dass er sich in skandinavischen Baumringen über viele hundert Jahre hinweg deutlich abzeichne. Im Hinblick auf Brückners Vermutung, dass ein Zusammenhang mit der Sonnenaktivität bestehe, fragen sie jedoch, welcher Index der Sonnenaktivität mit seinen Variationen dem Brückner-Zyklus folge. Die hier vorgelegten Ergebnisse beantworten diese Frage.
|
|
|
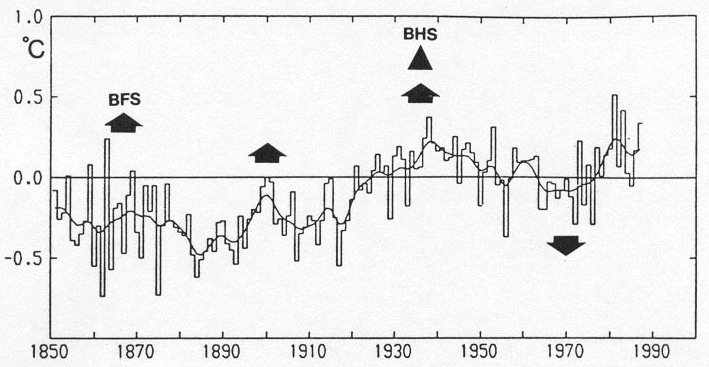
Abb. 9: Zeitreihe 1850 bis 1987 der jährlichen Mittel der an der Erdoberfläche gemessenen Temperatur der nördlichen Hemisphäre nach P. D. Jones [40]. Nullphasen der Zyklen Grosser Finger (BFS) sind durch Pfeile angezeigt. Die Nullphase einer hierarchisch übergeordneten Grossen Hand (BHS), die einen Phasensprung ausgelöst hat, ist durch ein Dreieck gekennzeichnet. Vor BHS fallen die BFS mit Maxima der geglätteten Temperaturkurve zusammen, danach mit Minima. Der nächste Temperaturtiefpunkt ist um 2007 zu erwarten. |
Bei dem in Abb. 9 gezeigten Beispiel handelt es sich um die Zeitreihe der jährlichen Mittel der an der Erdoberfläche gemessenen Temperatur der nördlichen Hemisphäre nach P. D. Jones [40]. Die Pfeile kennzeichnen Nullphasen der Zyklen Grosser Finger. Das Dreieck im oberen Bereich weist auf das Datum 1933 der Nullphase einer Grossen Hand hin. Vor 1933 fällt jeweils die Nullphase Grosser Finger mit Temperaturmaxima zusammen, während sie danach mit einem Temperaturminimum einhergeht. Hier handelt es sich offensichtlich um einen Phasensprung. Experimente mit elektronischen und mechanischen Regulationsmechanismen haben gezeigt, dass in Schwingungsknoten, in denen die Schwingung den Wert Null erreicht, Phasensprünge der Grösse Pi eintreten können [9]. Die Nullphase eines Grossen Fingers ist ein solcher Schwingungsknoten. Entscheidend ist aber, dass er 1933 mit der Nullphase einer Grossen Hand zusammenfällt. Hier bietet sich eine Erklärungsmöglichkeit für bisher als unerklärbar und unvorhersehbar angesehene Phasensprünge in solar-terrestrischen Zyklen. Die von der Zentralbewegung der Sonne abgeleiteten Zyklen bilden, wie wir noch sehen werden, ein Fraktal, das hierarchisch aufgebaut ist. Nullphasen von Zyklen auf einer höheren hierarchischen Ebene, wie der Grossen Hand, sind dominant und können bei untergeordneten Zyklen, wie dem Grossen Finger, Phasensprünge der Grösse Pi auslösen. Dass dies so ist, werden wir in einer ganzen Reihe von Beispielen sehen. Da der nächste Schwingungsknoten der Grossen Hand nicht vor dem Jahre 2111 erreicht wird, ist damit zu rechnen, dass die auf das Jahr 2007 fallende Nullphase eines Grossen Fingers mit einem weiteren Temperaturtiefpunkt einhergehen wird.
Oft spielt auch die erste Oberschwingung von Fingerzyklen eine wichtige Rolle. So stehen Zyklen halber Grosser Finger mit einer Länge von 17,9 Jahren in einer engen Beziehung zu der Dicke von Warven des Saki-Sees auf der Krim, die nach W. B. Schostakowitsch [101] vom jährlichen Niederschlag abhängt. Die Untersuchung erstreckt sich auf die Jahre 700 bis 1894, also fast 12 Jahrhunderte. Die Nullhypothese, dass kein Zusammenhang bestehe, ist auf dem Niveau P = 10-7 widerlegt worden. Wegen der Einzelheiten verweise ich auf meinen Beitrag zu der NASA Konferenzveröffentlichung "Climate Impact of Solar Variability" [62].
|
|
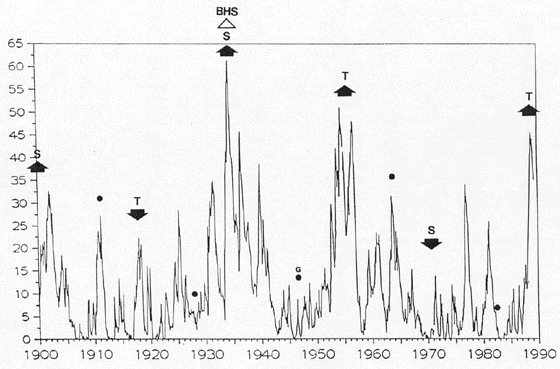
Abb. 10: Palmer-Dürre-Index für die USA. Die vertikale Achse gibt an, welcher Prozentsatz der für die Landwirtschaft erschlossenen Gebiete von Dürre heimgesucht wurde. Die Epochen der Nullphasen (S) und Mittelphasen (T) Grosser Finger sind durch Pfeile markiert. Die Nullphase einer Grossen Hand (BHS) ist durch ein offenes Dreieck gekennzeichnet. |
|
Nach BHS ist die Zuordnung der Phasen Grosser Finger zu den Dürreextrema genau umgekehrt wie davor. Die nächste Nullphase S um 2007 wird voraussichtlich in den USA mit feuchtem Klima einhergehen. |
|
Abb. 10 zeigt den Palmer-Dürre-Index für die USA. Von der vertikalen Achse ist abzulesen, welcher Prozentsatz der für die Landwirtschaft erschlossenen Gebiete von Dürre heimgesucht wurde. Die Epochen der Nullphasen Grosser Finger (S) und der Mittelphasen (T) sind durch Pfeile angezeigt. Vor der Nullphase 1933 der Grossen Hand, die durch ein offenes Dreieck markiert ist, fallen Nullphasen der Grossen Finger mit Dürremaxima und Mittelphasen mit Dürreminima zusammen. Nach dem Phasensprung 1933 ist es genau umgekehrt. Die Farmer in den USA können hiernach erwarten, dass die nächste Nullphase eines Grossen Fingers im Jahre 2007 mit relativ feuchtem Klima einhergehen wird. Was bedeuten nun die schwarzen Punkte, die abwechselnd mit Maxima und Minima der Kurve einhergehen und 1933 ebenfalls einen Phasensprung zeigen? Sie kennzeichnen den Goldenen Schnitt zwischen den Null- und Mittelphasen der Grossen Finger. Damit hat es folgende Bewandtnis: Die fünfzählige Symmetrie in der Dynamik der Sonnenschwingung stellt eine Beziehung zum Goldenen Schnitt her, denn dieses Teilungsmass ist eng mit der Zahl 5 verknüpft [45]. Zeichnet man in ein regelmässiges Fünfeck, die naheliegendste Verkörperung der Fünfzahl, alle Diagonalen ein, so erscheint ein regelmässiges Sternfünfeck. Dieses Pentagramm schliesst in seinem zentralen Teil ein weiteres regelmässiges Fünfeck ein, in welchem man wiederum die Diagonalen ziehen kann, die erneut ein Pentagramm bilden. Dieser iterative Prozess lässt sich ins Unendliche fortsetzen. In jedem Fall teilen sich die Diagonalen, die das Pentagramm bilden, wechselseitig im Verhältnis des Goldenen Schnitts.

Wie in Abb. 11 illustriert ist, verhält sich der kleinere Teil - Minor - zu dem grösseren Teil - Major - wie der grössere Teil zum Ganzen.N. Kolmogorov [47], V. I. Arnol’d [1] und J. Moser [79] haben darüber hinaus theoretisch nachgewiesen, dass die Stabilität des Sonnensystems vom Goldenen Schnitt abhängt. Dies ist wichtig, da wir seit den Arbeiten von G. J. Sussman und J. Wisdom [110] sowie J. Laskar [67] wissen, dass die Bahnen aller Planeten chaotisch sind. In meiner 1995 veröffentlichten Arbeit "Die kosmische Funktion des Goldenen Schnitts" [64] habe ich praktisch gezeigt, wie der Goldene Schnitt durch die Proportionierung der Planetenentfernungen dem Chaos entgegenwirkt und so zur Stabilisierung des Sonnensystems beiträgt. Die Fünfzahl ist tief in der Natur verankert. Es gibt nicht vier, sondern fünf physikalische Kräfte. Wir haben nur vergessen, dass hinter Elektrizität und Magnetismus verschiedene Kräfte stehen. Maxwell hat sie so vereinigt, wie später der Elektromagnetismus mit der schwachen Kraft vereinigt worden ist [44].
|

|
Abb. 12: Wasserspiegel der Grossen Seen Michigan und Huron. Nach BHS 1933 (schwarzer Pfeil) fallen die tiefsten Wasserstände mit Nullphasen der Zyklen Grosser Finger (S) und die höchsten Wasserstände mit den Mittelphasen (T) zusammen. Die flachen Dreiecke weisen auf Zwischenmaxima der Wasserstände hin, die mit dem Minor (0,382) des Goldenen Schnitts zwischen den Phasen S und T korreliert sind. |
|
Bei einer Extrapolation ist ein besonders niedriger Wasserstand um 2007 und ein besonders hoher Wasserstand um 2025 zu erwarten |
|
Abb. 12 nach R. Mogey [78] zeigt ein weiteres praktisches Beispiel, den Wasserspiegel der Grossen Seen Michigan und Huron. Nach der Nullphase der Grossen Hand 1933, die durch einen schwarzen Pfeil gekennzeichnet ist, fallen die tiefsten Wasserstände mit Nullphasen der Zyklen Grosser Finger (S) und die höchsten Wasserstände mit den Mittelphasen (T) zusammen. Hiernach ist ein besonders niedriger Wasserstand um 2007 und ein besonders hoher Wasserspiegel um 2025 zu erwarten. Die flachen Dreiecke weisen auf Zwischenmaxima hin, die mit dem Goldenen Schnitt zusammenhängen. Die Zahl 0,382 kennzeichnet, wie wir schon in Abb. 11 gesehen haben, den Minor des Goldenen Schnitts. Suchen wir den Minor einer Strecke, eines Zyklus oder irgendeiner anderen abgegrenzten Struktur, die als Ganzes angesehen werden kann, so ergibt er sich durch die Multiplikation der entsprechenden Grösse mit 0,382. Den Major erhalten wir durch Multiplikation mit 0,618.
Der Goldene Schnitt spielt auch in solaren Zyklen eine wesentliche Rolle. Aus den seit 1750 vorliegenden zuverlässigen Sonnenfleckendaten ergibt sich eine durchschnittliche Länge des ansteigenden Teils des 11-jährigen Zyklus von 4,3 Jahren [73]. Der Minor des Zyklus von 11,05 Jahren ist mit 4,2 Jahren praktisch gleich lang. Das Maximum des kurzen Sonnenfleckenzyklus fällt also mit dem Minor des Zyklus zusammen. Der absteigende Teil des Zyklus hat die Länge des Major. Dies trägt zur Stabilisierung der Sonnenaktivität bei, die durch Instabilitätsphänomene gekennzeichnet ist. Zyklen der magnetischen Aktivität sonnenähnlicher Sterne zeigen die gleiche vom Goldenen Schnitt geprägte Struktur [64].
|
|
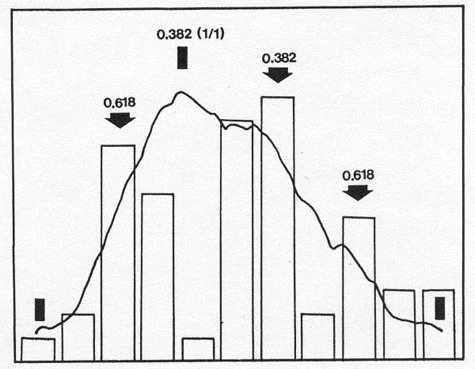
Abb. 13: Das Histogramm nach EOS [18] zeigt, wie sich besonders energetische Sonneneruptionen auf den 11-jährigen Sonnenfleckenzyklus verteilen. Major (0,618) und Minor (0,382) des Goldenen Schnitts innerhalb des aufsteigenden und des absteigenden Subzyklus setzen die Akzente. Das Maximum des Fleckenzyklus fällt auf dessen Minor 0,382. Es fällt auf, dass energetische Eruptionen das Maximum der Sonnenflecken meiden.
|
Das Histogramm in Abb. 13 nach EOS [18] zeigt, wie sich besonders energetische Eruptionen auf den 11-jährigen Zyklus verteilen. Die Akzente werden wieder durch den Goldenen Schnitt gesetzt, und zwar innerhalb der Subzyklen des aufsteigenden und absteigenden Teils des Gesamtzyklus. Dieses Muster kehrt in terrestrischen Zyklen wieder.
|
|
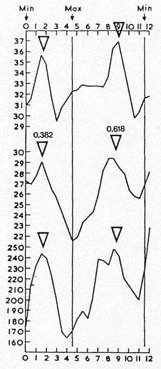
Abb. 14: Die drei Kurven nach H. H. Lamb [52] verbinden den 11-jährigen Sonnenfleckenzyklus mit der Gewittertätigkeit in Mitteleuropa. Im Kopf der Graphik sind die aufeinanderfolgenden Minima und das dazwischen liegende Maximum des jeweiligen Fleckenzyklus durch Pfeile markiert. Die obere Kurve gibt für 1810 - 1934 die Zahl der Tage mit Gewitter in Kremsmünster an, die mittlere Kurve stellt die Gewitterhäufigkeit in Wien für 1878 - 1934 dar
und die untere Kurve gibt die Zahl der Blitzeinschläge je 1 Million Häuser in Bayern für 1833 - 1879 wieder. Die Maxima in allen drei Kurven fallen mit 0,382 des aufsteigenden Zyklus und 0,618 des absteigenden Zyklus zusammen. Offene Dreiecke weisen auf diese Schnittstellen hin.
|
Die drei Kurven in Abb. 14 nach H. H. Lamb [52 ] verbinden den 11-jährigen Sonnenfleckenzyklus mit der Gewittertätigkeit in Mitteleuropa. Im Kopf der Graphik sind die aufeinanderfolgenden Minima und das dazwischen liegende Maximum des jeweiligen Fleckenzyklus durch Pfeile markiert. Die obere Kurve gibt für 1810 bis 1934 die Zahl der Tage mit Gewittern in Kremsmünster an, die mittlere Kurve stellt die Gewitterhäufigkeit in Wien für 1878 bis 1934 dar, und die untere Kurve gibt die Zahl der Blitzeinschläge je 1 Million Häuser in Bayern in den Jahren 1833 bis 1879 wieder. Die Maxima aller drei Kurven stimmen mit Minor 0,382 und Major 0,618 der Subzyklen des Sonnenfleckenzyklus überein, die durch offene Dreiecke gekennzeichnet sind.
Der magnetische Zyklus von 22,1 Jahren, auch Hale-Zyklus genannt, ist der eigentliche Zyklus der Sonnenfleckenaktivität. Fleckengruppen setzen sich aus nordmagnetischen und südmagnetischen Flecken zusammen, die bipolar angeordnet sind. Während eines 11-jährigen Zyklus laufen bei der Rotation der Sonne entweder die Nordpole oder die Südpole ständig voraus. Nach 11 Jahren kehrt sich diese Polarität um. Es vergehen also zwei 11-jährige Zyklen, bis die gleiche Anordnung wieder erscheint. Berechnen wir nun den Major des Zyklus des Grossen Fingers, so erhalten wir genau die Länge des Hale-Zyklus (35,76 Jahre ´ 0,618 = 22,1 Jahre). Auch dieser Zusammenhang trägt dazu bei, dass die Instabilität, die der Sonnenaktivität inhärent ist, nicht überhand nimmt. Der Hale-Zyklus zeichnet sich auf der Erde deutlich ab in der Lufttemperatur, die an Bord von Schiffen gemessen wird [9], in der Lufttemperatur Mittelenglands [72] und im Dürre-Index der U.S.A. [77]. Auch der Major des Zyklus der Grossen Hand führt zu einem interessanten Ergebnis. Er liegt bei 110,5 Jahren. Japanische Forscher haben 1995 bei Frequenzanalysen von Sonnenfleckendaten einen Zyklus genau dieser Länge gefunden [120].
Inhalt
1) Variationen der "Solarkonstanten" im 11-jährigen Sonnenfleckenzyklus und klimatische Auswirkungen
2) Gleissberg-Zyklus der Sonnenaktivität und Klimaschwankungen
3) Variation der ultravioletten Strahlung der Sonne und Klimamodelle
4) Kosmische Strahlung, Sonnenwind und Wolkenausbreitung
5) Misserfolg der Klimavorhersagen von IPCC-Wissenschaftlern
6) Zyklen der Sonnenschwingung beeinflussen Sonnenfleckentätigkeit und Klima
7) Zyklus von 36 Jahren in Sonnenaktivität und Klima
8) Zyklen "Kleiner Finger" als Grundlage zuverlässiger Vorhersagen von Sonneneruptionen und Klima
9) Literaturangaben
Der Artikel in englischer Sprache - english version bei Daly, AU
Solar Activity controls El Niño and La Niña neu von Dr. Landscheidt





