Fractales en la secundaria
- La dimensión no tiene por qué ser un número entero -
En este apartado vamos a introducir un nuevo concepto. Para ello nos van a hacer falta unos conocimientos previos. Estos son:

Para introducir este concepto, se recomienda plantear el siguiente ejemplo.

"Dada una circunferencia de radio r>0 arbitrario, mide su perímetro". Si el alumno no conociera la fórmula del perímetro de la circunferencia, se le podría proponer la siguiente manera de proceder: Inscribir polígonos regulares en ella, de los cuales sí se sabe calcular su perímetro, y tomarlos cada vez con más lados, para acercarse más a esa medida que se busca.

Gráficamente, el proceso sería :



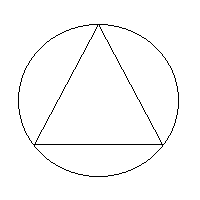
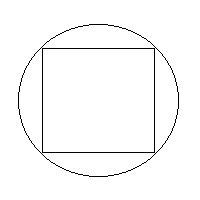
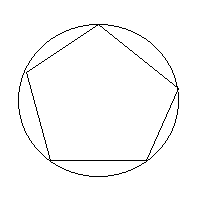
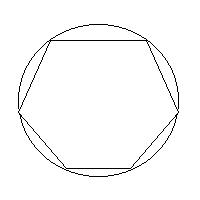
Al final del proceso, llegamos a que el perímetro de la circunferencia tiene el valor r. Pero ahora te dan otra figura algo más complicada, y te piden, de nuevo, que midas el perímetro. La figura es la siguiente :

Curva de Koch

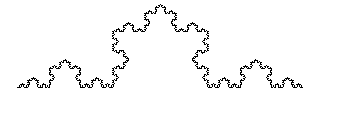
El proceso de construcción de esta figura es el siguiente:
Cogemos el segmento unidad y lo dividimos en tres partes iguales. Eliminamos el tercio central, y levantamos un triángulo equilátero de lado 1/3 en el hueco (el triángulo no tendrá base, claro)

Repitiendo infinitas veces el proceso con cada segmento se obtiene la curva de Koch.

De nuevo, la idea de ir aproximando la medida de la figura parece razonable, usando para ello algo cuyo perímetro sea conocido. Por ejemplo, usamos reglas cada vez más pequeñas.

Regla escala 1/3
Regla escala 1/9
Regla escala 1/27


Para aproximar mejor, ampliamos la figura, y ... aparecen detalles que no percibíamos al principio. La figura, en cierto sentido, se repite. Y si la volvemos a ampliar, aparecen más detalles, y de nuevo más ...

Esto no sucedía con la circunferencia. Si la circunferencia la vamos ampliando sucesivamente, vamos perdiendo la visión de una circunferencia, y lo que vemos es, localmente, cada vez más parecido a una recta, y esto es precisamente lo que nos permite medir con relativa facilidad su perímetro.

La dificultad para medir el perímetro de la curva de Koch parece estar ligada al hecho de que la figura se repita en cada uno de sus trozos infinitas veces. El significado de este hecho será explicado a continuación.

Para poder dar esta explicación, hay un concepto que debe quedar claro, y es el de figura autosemejante.

Tenemos una figura cualquiera. Si las partes de dicha figura son pequeñas réplicas del total, diremos que la figura es autosemejante . Diremos que una figura es estrictamente autosemejante si la figura se puede descomponer en partes que son réplicas exactas del total, y si cualquier parte arbitraria contiene una réplica exacta de la figura total.

Una vez este concepto ha quedado claro, veamos lo siguiente.

Tenemos una línea :
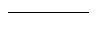
ahora la dividimos en tres partes iguales :
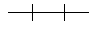
y de esas partes cogemos una cualquiera :

Este trozo de línea es, claramente, semejante a la línea original. Lo único que las distingue es un factor de escala 1/3 (una reducción a una tercera parte del tamaño original).

Hagamos lo mismo con un cuadrado :
Este cuadrado es semejante a este pequeño:

Y ahora con un cubo :



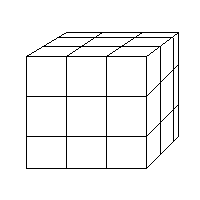
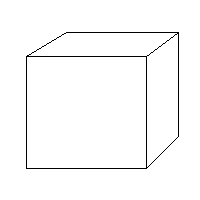
De nuevo, esta figura es semejante a la figura original.

Podíamos haber usado, en vez de un factor de escala 1/3; 1/2, 1/4, o, en general, 1/n, siendo n perteneciente a N* (N* = N \ {0}).
En cualquier caso, la figura obtenida es semejante a la figura original.
Vamos ahora a fijarnos en el siguiente hecho.
Cuando hemos dividido la línea, me han quedado tres trozos semejantes a ella. Si yo ahora cojo uno de esos trozos, necesito exactamente 3 (3^1) para reconstruir la construcción original. En el caso del cuadrado, necesito 3x3 ( 3^2 ) trozos para reconstruir la figura original. Y, en el caso del cubo, necesito 3x3x3 ( 3^3 ) trozos para la reconstrucción del original.

Es decir, se observa una relación entre la escala, el número de trozos en que divido la figura, y lo que (tradicionalmente) se conoce como dimensión del objeto. Esta relación se puede expresar de la siguiente forma :



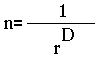
donde n es el número de trozos en que dividimos la figura, r es la razón de escala, y D es la dimensión.

En los ejemplos, tenemos que D=1 para la línea, D=2 para el cuadrado, y D=3 para el cubo. Es decir, el exponente que aparece en la fórmula se corresponde con los valores que nos son conocidos de su dimensión.

Ahora, cabe preguntarse : ¿y si tomamos otra escala?. ¿Seguirá siendo válida la fórmula?. Esta cuestión puede verse contestada en la siguiente tabla:

OBJETO N° PIEZAS ESCALA D (OBTENIDO CON LA FORMULA)
LINEA 3^1 1/3 1
2^1 1/2 1
5^1 1/5 1
11^1 1/11 1
.... .... ...
n^1 1/n 1
CUADRADO 3^2 1/3 2
2^2 1/2 2
5^2 1/5 2
11^2 1/11 2
.... .... ...
n^2 1/n 2
CUBO 3^3 1/3 3
2^3 1/2 3
5^3 1/5 3
11^3 1/11 3
.... .... ...
n^3 1/n 3

En la tabla vemos que la fórmula es consistente, sea cual sea la escala en la que dividamos nuestra figura.

Ahora, abordando el problema planteado al principio, ya podemos hacer algunas cosas. Según la definición de figura autosemejante, descubrimos que la curva de Koch que nos han dado cumple esa propiedad: es autosemejante. Así pues, vamos a poder aplicar la fórmula dada antes.

Fijándonos bien en esta curva, observamos que está compuesta de n=4 trozos a escala r=1/3 de la original. Pero también podríamos tomarla compuesta de n=16 trozos a escala r=1/9 de la original. En general, se podría tomar compuesta de n=4^k trozos a escala r=(1/3)^k de la original.

En el primer caso, obtenemos : 4 = 3^D . Para despejar D de la ecuación, tomamos a ambos lados logaritmos. Así, nos queda : log(4) = Dxlog(3)

D=log(4)/log(3)= 1. 2619

Evidentemente, D no es un número entero, y eso nos hace dudar de la validez de la fórmula, así que lo comprobamos para más casos.

Si n=16 y r=1/9, tenemos : log(16) = Dxlog(9)



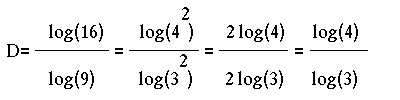
...... (repetimos k veces)

Si n=4^k y r=(1/3)^k, tenemos : log(4^k) = Dxlog( (1/3)^k )



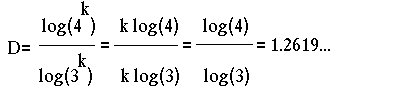
Este resultado es válido para cualquier valor de k.
Es decir, tenemos que la dimensión de la curva de Koch es D=log(4)/log(3)

Antes de pasar a algo nuevo, conviene afianzar este concepto, y, para ello, es conveniente realizar los siguientes ejercicios. Vamos a explicar cómo se construyen algunos fractales autosemejantes, y a continuación se pide al alumno que calcule la dimensión de estos conjuntos.

Tenemos el intervalo [ 0, 1]. Lo dividimos en tres partes iguales, y quitamos el tercio central. Así, nos quedan dos intervalos de longitud 1/3. Ahora, con estos dos intervalos repetimos el proceso: cada uno de ellos los dividimos en tres partes iguales y quitamos los segmentos centrales. Vamos procediendo de esta manera, dividiendo cada segmento en tres iguales y quitando el central. Así, en el paso k, tendremos 2^k segmentos de longitud ( 1/3 )^k. El conjunto resultante de realizar este proceso infinitas veces es conocido como el conjunto de Cantor. Sabiendo como se construye, calcula su dimensión.

Tenemos un triángulo equilátero de lado 1. Lo dividimos en cuatro triángulos iguales, uniendo los puntos medios de los lados. De estos cuatro triángulos, eliminamos el triángulo central. Así, nos quedan tres triángulos a escala 1/2 del original. Con los tres triángulos que nos quedan, repetimos el proceso: cada uno de ellos lo dividimos en cuatro partes iguales uniendo los puntos medios de los lados, y eliminamos los triángulos centrales. Así, tendremos 9 triángulos a escala 1/4 del original. Seguimos haciendo este proceso. En el paso k, tendremos 3^k triángulos a escala (1/2)^k. Tras repetir este proceso infinitas veces, se obtiene el conjunto conocido como triángulo de Sierpinski. Conocido el proceso de construcción, calcula su dimensión.

Tenemos un cuadrado de lado 1. Lo dividimos en nueve cuadrados iguales. De estos nueve cuadrados, eliminamos el cuadrado central. Así, nos quedan ocho cuadrados a escala 1/3 del original. Con los ocho cuadrados que nos quedan, repetimos el proceso : cada uno de ellos lo dividimos en nueve iguales, y eliminamos los cuadrados centrales. Así, tendremos 64 cuadrados a escala 1/9 del original. Seguimos haciendo este proceso. En el paso k, tendremos 8^k cuadrados a escala (1/3)^k. Tras repetir este proceso infinitas veces, se obtiene el conjunto conocido como la alfombra de Sierpinski. Conocido el proceso de construcción, calcula su dimensión.

De vuelta a GeoCities