a) Algunas consideraciones
Cuando se escucha a los alumnos hablar sobre la utilización de letras, es común oirles decir frases como:
En muchas oportunidades, estas frases se transforman en letras
que aparecen, a los ojos de algunos docentes, como indicios de
que los alumnos comprenden el significado del lenguaje algebraico
y casi suficientes para que reconozcan la necesidad o la
conveniencia de la utilidad de dicho lenguaje. Una considerable
cantidad de problemas que pueden resolverse a través de
ecuaciones o inecuaciones, parecen ser el final de obra para este
proceso.
La experiencia en el aula muestra que esto no es suficiente dado
que no se tomaría en cuenta una serie de reflexiones que se
suponen aptas para que los alumnos podrán hagan por sí mismos.
Por ejemplo: la igualdad. La que los alumnos definen hasta el
momento en que se comienza a trabajar el lenguaje algebraico, es
aritmética y, por lo tanto, sinónimo de resultado numérico,
como en:
3 . 7 = 21
o de secuencia de pasos intermedios para la obtención de un resultado numérico:
3 . 2 + 4 . 5 = 6 + 20 = 26
Este sentido del signo "=" se mantiene en álgebra cuando se trabajan tautologías:
2x + 3 = x + x + 3
pero no en las ecuaciones en donde no expresa una conexión de equivalentes sino un condicionamiento para la incógnita.
Aún más consideraciones presenta la utilización y
significación de las letras.
Si se presentan a los alumnos situaciones tales como:
se están presentando letras desconocidas pero evaluables que
pueden ser reemplazadas por un número a la espera de obtener un
valor numérico: letras evaluadas.
Si se les plantea, en cambio:
Si a + b = 10, ¿cuál es el valor de a + b - 1?
no se espera un resultado numérico para ellas: son letras
ignoradas.
En otros casos, las letras son trabajadas como objetos. Es el
caso de:
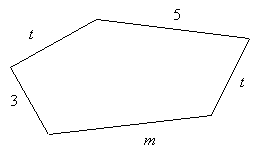
¿Cuál es el perímetro del polígono?

En otras ocasiones se les propone como generalización de números, como los enunciados de propiedades:
En la suma de números racionales, siempre a + b = b + a
Un nuevo rol cumple en el contexto funcional, en el cual es una variable que representa un conjunto de valores no especificados.
Es necesario que los docentes tengan presente estas opciones para que, al trabajar con los alumnos, puedan disponer de los recursos didácticos necesarios para detectar cuáles de los aspectos le resultan más complicados de elaborar y además considerar en la planificación que el trabajo en los procesos de enseñanza y de aprendizaje del lenguaje algebraico necesitan un espacio propio.
b) El trabajo en el aula
Entre las múltiples opciones con que se cuenta para introducir en el lenguaje algebraico a los alumnos, en esta propuesta se elige plantearles la necesidad de su uso. El objetivo es que lo interpreten como una forma más clara y simplificada de calcular y escribir, por ejemplo, determinadas relaciones.
Novak (1991, p. 216) rescata algunos argumentos de Ausubel acerca de cómo aprenden las personas y de él transcribe el siguiente principio:
"De todos los factores que influyen en el aprendizaje, el más importante consiste en lo que el alumno ya sabe. Averígüese esto y enséñese
consecuentemente".
Se trata entonces de comenzar con algunas actividades que apelen a la revisión de saberes previos de los alumnos y cimentar el trabajo en el aula en función de esto; por ello se plantean las primeras actividades haciendo hincapié en otros lenguajes que ellos ya conocen y que manejan a diario, además del que utilizan para hablar y escribir.
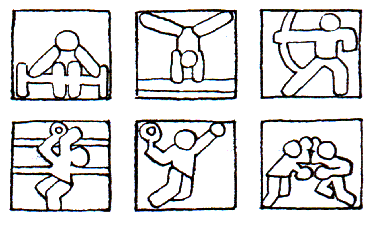
1) Cada uno de los siguientes símbolos representa un deporte. Identificalos usando una sola palabra.
 (1)
(1)
2) Quienes no pueden oír o hablar se comunican con un lenguaje de signos que se representan con las manos. Cada signo se corresponde con una letra del alfabeto o una palabra entera. Hay varios sistemas distintos. En la siguiente figura se muestran las letras del alfabeto en el sistema de nuestro país. Decí "Buenos días" usando este lenguaje.

3) A mediados del siglo XIX se inventó el telégrafo eléctrico, que transmite por cable una corriente eléctrica mediante impulsos largos y cortos, utilizando el sistema del norteamericano Morse.
Representando los impulsos largos por rayas y los cortos por puntos, la simbolización de las letras del alfabeto es la siguiente:

Utilizando este sistema, descifrá el siguiente mensaje:
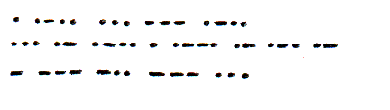
Las actividades presentadas permitirán discutir en clase por qué creen los alumnos que la matemática requiere un lenguaje propio y qué tipo de símbolos utilizará, del mismo modo que cada uno de los lenguajes conocidos cuentan con los propios. Los símbolos: ¿son una ayuda para comprender mejor el problema, para escribirlo en forma más clara o simplificada?
Para dar respuesta a la pregunta, se presentan algunos problemas que pueden resolverse a través de estrategias ya conocidas, incluso sin necesitar el lenguaje simbólico, y que no descartan el ensayo y error.
4) Completá la siguiente tabla, considerando que la figura que se analiza es un rectángulo y que uno de sus lados supera en 4 unidades al otro lado.
|
Perímetro |
Lado 1 |
Lado 2 |
|
18 |
|
|
|
22 |
|
|
|
52 |
|
|
|
57 |
|
|
|
60 |
|
|
|
22,8 |
|
|
|
48,8 |
|
|
|
65,2 |
|
|
|
68,44 |
|
Los primeros renglones de la tabla pueden resolverse, tal como se indicó, por ensayo y error o "tanteo". Pero a medida que se avance en la resolución, los alumnos notarán que hay un esquema que se repite, estarán realizando las mismas operaciones en uno u otro renglón para poder completar las celdas. Ellos mismos notarán la conveniencia de encontrar una fórmula general que les permita responder los renglones subsiguientes, sin tener que repetir todo el razonamiento elaborado para el caso anterior.
Puede, sin embargo, no plantearse esta inquietud en primera instancia; para ello, se colocaron en los últimos renglones valores no enteros para el perímetro, lo cual dificulta responder a las medidas de los lados sólo utilizando ensayos sucesivos.
5)
a) Calculá el área sombreada, según sean a y b:

| a | b | Área |
| 3 | 1 | |
| 4 | 2 | |
| 7,1 | 3 | |
| 10,4 | 4,6 |
b) Agregá a la tabla los renglones que consideres necesarios para poder elaborar una conjetura acerca de cuál es la fórmula para calcular el área de la región sombreada cualesquiera sean los valores de a y b.
6)
a) ¿Cuántos cuadrados observás en un tablero de ajedrez?
Podés ayudarte completando la siguiente tabla en la que se presentan diversas figuras o "tableros" más sencillos, cuyos lados se incrementan uno a uno.
|
Figura |
Número de cuadrados de lado 1 |
Número de cuadrados de lado 2 |
Número de cuadrados de lado 3 |
Número de cuadrados de lado 4 |
.... |
Número total de cuadrados |
|
|
1 |
0 |
0 |
0 |
|
1 |
|
|
4 |
1 |
0 |
0 |
|
5 |
|
|
9 |
4 |
|
|
|
|
|
|
16 |
9 |
|
|
|
|
|
|
25 |
16 |
|
|
|
|
|
......... |
|
|
|
|
|
|
b) Buscá alguna regla que te permita calcular el número de cuadrados en cualquier caso.
Continuando una línea similar a lo mencionado anteriormente, se plantea en este caso, ya en forma explícita, la necesidad de una fórmula general que permita resolver el problema, si antes no había sido visto como una conveniencia.
El nivel de dificultad que presenta la obtención de una fórmula general, si se trabaja dentro del contexto del lenguaje coloquial, es mayor que el que aparece en el contexto gráfico. Por eso sugerimos un paso intermedio como este:
7) Las siguientes son ecuaciones que, por sí mismas, quizás parecen incompletas a pesar de que resumen el sentido de determinados enunciados:
a) 3b = 21
b) l² = 4
c) p + 220 = 500
d) x³ = 27
e) 2x + 2y = 10
Relacionalas con algún enunciado que aparece a continuación:
El área de un cuadrado de lado l es igual a 4
El volumen de un cubo de arista x es igual a 27
El costo de tres lapiceras es de $21
Tendientes a cumplir los mismos objetivos, se pueden presentar algunos de los problemas más comunes a los que los estudiantes están acostumbrados a trabajar por aparecer en distintos libros de texto:
8) Tres amigos compran un billete de lotería que resulta premiado con $500.000. Calculá cuánto debe corresponderle a cada uno, sabiendo que el primero aportó el doble que el segundo y éste el triple que el tercero.
9) El promedio de Sebastián entre sus 4 notas en Historia era de 7,80 hasta que su profesora le entregó su última evaluación. A partir de ese momento su promedio fue de 6,64. ¿Cuál fue la nota de la evaluación?
Siguiendo a éstas, las actividades que se plantean a continuación presentan de forma más directa la necesidad de un nuevo tipo de resolución:
10) La suma de seis números es par. El producto de los cuatro primeros es impar. Y el último es par. ¿El quinto número es par o impar?
11) Al comprar un determinado artículo te ofrecen un 15 % de descuento si pagás en efectivo y te aclaran que falta agregarle el 21 % de I.V.A.
a- ¿Qué te conviene más: que primero te hagan el descuento o al revés?
b- ¿Depende del precio del artículo?
c- ¿Depende de los valores de los porcentajes?
d- Fundamentá todas las respuestas anteriores en una conclusión final.
En ambas situaciones, pueden recurrir al uso de algunos casos particulares que le permitan comenzar a realizar algunas conjeturas, a captar mejor el significado del problema para que dichas conjeturas sean más fundadas. Nuevas y cuidadosas particularizaciones, con la vista puesta más bien en el "por qué" que en el "qué" pueden conducir a una intuición clara de lo que está ocurriendo realmente.
Pero en ninguno de los enunciados aparecen valores determinados como datos (no hace referencia a un número par o impar en particular ni se indica el precio del artículo que se quiere comprar). La particularización que realicen sólo será eso: un caso particular.
Se plantea entonces el interrogante: ¿cómo se puede asegurar que la respuesta a la que se creyó llegar seguirá manteniéndose a medida que se consideren otros casos particulares?, es decir, ¿cómo se puede asegurar que la respuesta valdrá en todos los casos?. Y lo más importante se dará al plantearse: ¿cuál es el concepto matemático que fundamenta la respuesta?
Elegir ejemplos al azar puede ser una buena manera de hacerse idea del significado de un problema, así como de ver si cierta afirmación o conjetura tiene visos de ser verdad, pero cuando lo que se buscan son leyes generales, lo más seguro para dar con ellas es particularizar de una manera ordenada, sistemática e ingeniosa.
En síntesis, se usa la particularización:
· Aleatoriamente, para entender el significado del problema
· Sistemáticamente, para preparar el terreno a la generalización
· Ingeniosamente, para comprobar la generalización.
Particularizar da una idea de lo que está pasando; el detectar alguna ley oculta (generalización) y formularla en palabras da lugar a una conjetura que puede ser examinada, cuestionada y modificada.
Generalizar significa descubrir alguna ley general que indique:
· Qué parece ser cierto (una conjetura)
· Por qué parece que es cierto (una justificación)
· Dónde parece que es cierto, esto es, un planteamiento más general del problema (¡otro problema!)
Explicar el "por qué" significa hacerse una idea de alguna razón subyacente que justifique la veracidad de una conjetura, convencerse a sí mismo y convencer a los otros de que se pueden justificar los argumentos; está fundamentalmente basado en la idea de estructura matemática, una noción importante que se oculta detrás de los intentos de explicar por qué algo debe ser cierto y constituye un desarrollo del proceso de conjeturar.
Los ejemplos mencionados en la secuencia de actividades, pueden implementarse para concebir la necesidad de un lenguaje simbólico que resulta imprescindible al expresar las respuestas.
(1)Las imágenes que aparecen en las tres primeras actividades de la guía se encuentran en BECERRA SEPÚLVEDA, M.V. (1996): Matemáticas 2. Madrid, Mc Graw-Hill