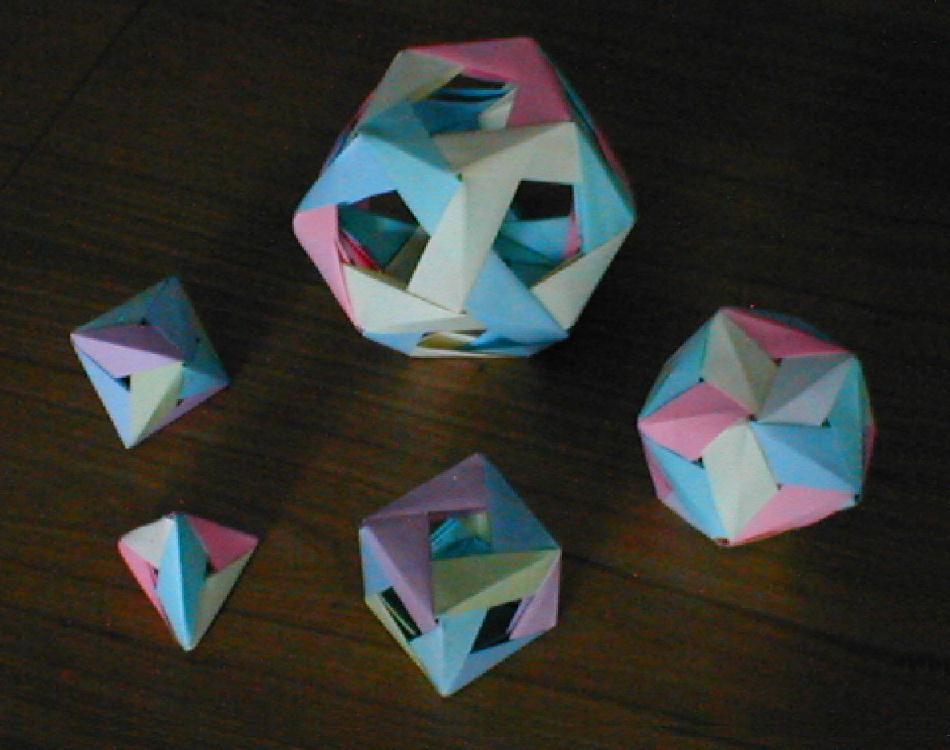
Uno de los objetivos de la utilización de esta técnica con docentes fue, en principio, un primer acercamiento al doblado de papel y el análisis desde lo matemático y desde lo didáctico que permite la práctica del Origami.
Considerando los modelos desarrollados a partir de módulos, pueden elaborarse construcciones de una variada gama de cuerpos geométricos. No obstante, la práctica se circunscribió a los poliedros regulares.
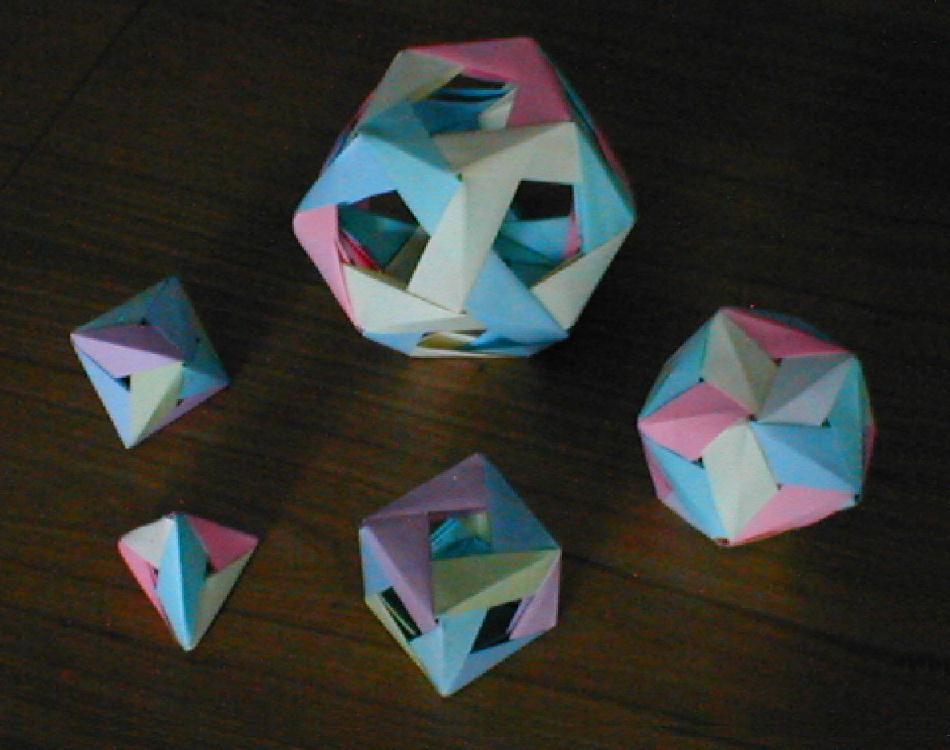
Una vez adquirida cierta destreza en el plegado y encastre, tuvo lugar el planteo de situaciones que dieran origen al análisis de los módulos empleados.
Éste tuvo como objetivo la toma de contacto con numerosas propiedades geométricas, algebraicas, relativas al número e, incluso, sobre funciones que se pueden encontrar en las mencionadas piezas.
Así, por ejemplo, se plantearon situaciones como: ¿Cuál es la mayor longitud que se puede considerar como lado de un cuadrado, de modo tal que el dodecaedro construido con módulos a partir de esa figura, quepa en una caja de un metro de alto, sabiendo que sus otras dimensiones no influyen en el traslado?


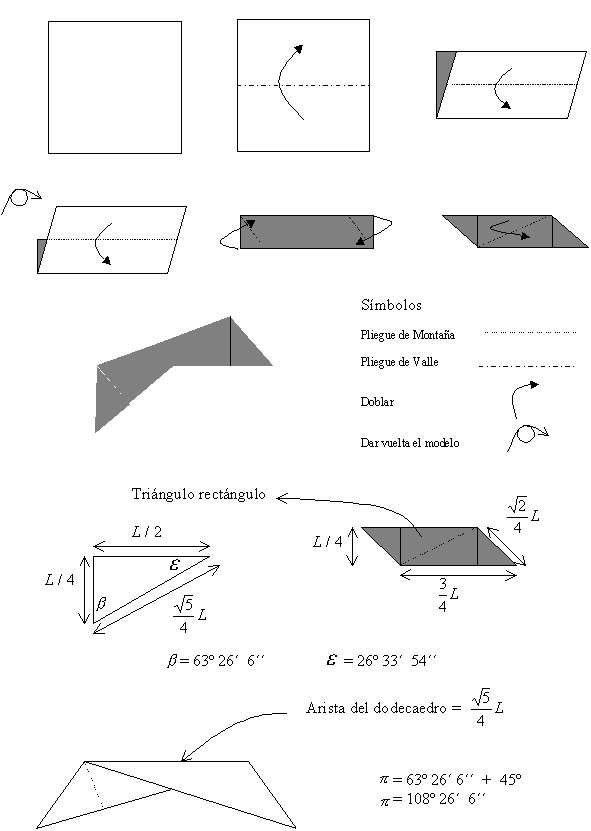
Para ello, resultó necesario no sólo el modelo de construcción del dodecaedro regular de acuerdo con algunas de las técnicas vistas, sino también el análisis de los módulos que lo constituyen, a partir de los conceptos matemáticos que requiere la tarea.
Como ejemplo, puede citarse un modelo de técnica de construcción y parte del análisis matemático que se desarrolló respecto del dodecaedro:
Este trabajo con los docentes permitió, además, establecer diferencias, semejanzas, ventajas y desventajas, que presentan cada una de estas construcciones respecto de los métodos convencionales.
También, se procuró con los docentes abordar con mayor profundidad los lineamientos generales de la postura didáctica basada en la utilización de materiales durante el proceso de enseñanza-aprendizaje, y los modelos de Origami como caso particular dentro de la variedad disponible.
Y respecto de la vivencia de las etapas mencionadas, cabe destacar también el análisis que tuvo lugar a partir del reconocido modelo de Van Hiele. De esta forma y siguiendo las pautas de la teoría, pudieron analizarse las actividades realizadas junto a los docentes, para verificar que partiendo de la manipulación de material se avanzó hasta el ordenamiento de propiedades.
De esta manera, se transitó desde el primer nivel de razonamiento planteado por el modelo de Van Hiele (reconocimiento) hasta el tercero (clasificación) alcanzando objetivos específicos en cada uno de los niveles.
De acuerdo con este modelo, la formación matemática que así se logra es valiosa puesto que proporciona un desarrollo en la percepción visual y espacial. Puede servir como vehículo para estimular y ejercitar habilidades generales de pensamiento y capacidades para la resolución de problemas. El ejercicio de la visualización, la representación y comparación de figuras en diferentes posiciones, permite el desarrollo del sentido espacial que parece necesario para interpretar, comprender y apreciar la geometría.
Por su parte, la utilización en la práctica con alumnos de Tercer Ciclo de la EGB, siguiendo el esquema aprestamiento-problema, ya descripto, permitió analizar el origen de algunas imperfecciones de los desarrollos e, incluso, descubrir o visualizar relaciones entre las figuras que quedan determinadas al desdoblar el módulo base.