DİJİTAL ELEKTRONİKTE SAYI SİSTEMLERİ

DİJİTAL ELEKTRONİK
Dijital Elektronik, Analog Elektronikten sonra çıkan en gelişmiş elektronik teknolojisidir. Bazı analog sinyallerin saklanması ve daha az kayıpla taşınmasında kullanılır. Ayrıca Şu anda kullansığınız bilgisayarında temeli Dijital Elektroniktir. Harddiskte saklanan bilgiler dijital kodlarla saklanır ve yine dijital kodlarla işlemcide işlenir. Bir kişinin Dijital elektronik öğrenmesi için ilk olarak sayı sistemlerini çok iyi bir şekilde bilmesi gerekir. Sayı sistemleri Dijital Elektroniğin temelidir. Şimdi Sayı sistemlerini ayrıntılı bir şekilde inceleyelim.

1 ) - Sayı Sistemleri :
Dijital eletronikte dört çeşit sayı sistemi kullanılmaktadır. Bunlar :

a) Desimal Sayı Sistemi    b) Binary Sayı Sistemi    c) Oktal Sayı Sistemi        d) Hexadesimal Sayı Sistemi

a) - Desimal Sayı Sistemi :
Desimal say sistemi normal sayma sayılardan oluşur. Yani, 0 1 2 3 4 5 6 7 8 9 sayılarından oluşur. On adet sayı bulunduğu için bu sayı sisteminin tabanı 10'dur. (158 10) şeklinde yazılır. Bu sayı sisteminde ise dört matematiksel işlem bilindiği gibidir.

b) - Binary Sayı Sistemi :
Binary sayı sisteminde iki adet sayı bulunur. Bunlar 0 ve 1 dir. Bu yüzden Binary sayı sisteminin tabanı 2'dir. (1011 2) şeklinde yazılır.Aşağıda Binary sayı sistemi ile toplama, çıkarma, çarpma ve bölme işlemleri görülmektedir.

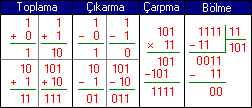
Binary sayının Desimal sayıya çevrilmesi :

101 2  Binary sayısını Desimal sayıya çevirelim.

1 x 2 ² + 0 x 2 ¹ + 1 x 2 º => 1 x 4 + 0 x 2 + 1 x 1 = 4 + 0 + 1 = 5 10 bulunur.

Desimal sayının Binary sayıya çevrilmesi :
Desimal sayı Binary sayıya çevrilirken Binary sayının tabanı olan 2'ye bölünür.
9 10 Desimal sayısını Binary sayıya çevirelim.

Tablodan görüldüğü gibi 9 sayısı 2 'ye bölünür. Bu işlem bölüm sıfır olana kadar devam eder. Kalan kutusundaki rakamlar aşağıdan yukarı doğru alınarak yan yana yazılır. Sonuç = 1001 2

c) - Oktal Sayı Sistemi :
Oktal sayı sistemindede 8 adet rakam bulunmaktadır. Bunlar 0 1 2 3 4 5 6 7'dir. Taban sayısı 8'dir. (125 8) şeklinde gösterilir. Aşağıda Oktal sayılarla toplama, çıkarma, çarpma ve bölme işlemleri görülmektedir.

Oktal sayının Desimal sayıya çevrilmesi :
25 8 oktal sayısını desimal sayıya çevirelim.

2 x 8 ¹ + 5 x 8 º  => 2 x 8 + 5 x 1 = 16 + 5 = 21 10 bulunur.

Desimal sayının Oktal sayıya çevrilmesi :
Desimal sayı Oktal sayıya çevrilirken Oktal sayının tabanı olan 8'e bölünür.
84 10 Desimal sayısını Oktal sayıya çevirelim.

Tabloda görüldüğü gibi 84 sayısı 8'e bölünür. Daha sonra bölüm kutusundaki sayı tekrar 8'e bölünür. (Bölüm sıfır olana kadar). Kalan kutusundaki sayılar aşağıdan yukarı doğru alınarak yan yana yazılır. Çıkan sayı oktal sayıdır. Sonuç = 124 8

d) - Hexadesimal Sayı Sistemi :
Hexadesimal sayı sisteminde 16 adet rakam bulunur.Bunlar 0 1 2 3 4 5 6 7 8 9 A B C D E F'dir. Tabanı ise 16'dır ve (1D2A 16) şeklinde yazılır. Aşağıda Hexadesimal sayılarlar toplama, çıkarma, çarpma ve bölme işlemleri görülmektedir.

Hexadesimal sayının Desimal sayıya çevrilmesi :
4F8 16 sayısını Desimal sayıya çevirelim.

4 x 16 ² + F x 16 ¹ + 8 x 16 º => 4 x 256 + F x 16 + 8 x 1 = 1024 + 240 + 8 = 1272 2 bulunur. Hexadesimal sayılarla hesap yapılırken harf olarak belirtilen sayıların rakama çevrilerek hesap yapılması daha kolay olacaktır. Örneğin (C = 12 , A = 10 , F = 15) gibi.

Desimal sayının Hexadesimal sayıya çevrilmesi :
Desimal sayıyı Hexadesimal sayıya çevirirken, Desimal sayı Hexadesimalin tabanı olan 16'ya bölünür. 100 10 Desimal sayısını Hexadesimal sayıya çevirelim.

Desimal sayı, bölüm sıfır olana kadar 16'ya bölünür. Daha sonra kalan kutusundaki sayılar aşağıdan yukarı doğru alınarak yan yana yazılır. Sonuç = 64 16

e) - Sayı Sistemlerinin Eşitlikleri :
Aşağıda, tüm sayı sistemlerinin birbirlerine olan eşitlikleri görülmektedir.