STEP 2:

Hand in the second worksheet with the graphic below:

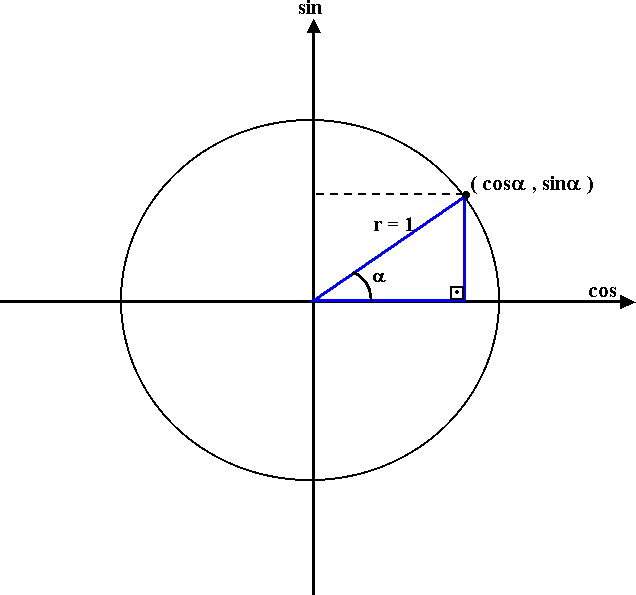
Notice that the first worksheet had no label on the axes. Now, after drawing a right angle triangle using one ratio as the hypotenuse, show that the point has abscissa equals to the value of the cosine of a and ordinate equals to the value of sine of a.
If necessary, review the concept of quadrants and the signs of the coordinates.
Invite the students to draw congruent triangles to the first one, using a pair of squares, with the ended point of the hypotenuse in different quadrants of the circle. They will see the symmetry related either to the axes or the origin and conclude that some angles can have negative values for their sines and cosines.
It's important to mention that these negative values are not for sine or cosine of the angle a, since its ended point is in the first quadrant. Show them that these new angles have a relationship with the angle a but they are different angles since each arc begins at the start point. Show them that it would be impossible to draw a right angle triangle with one of its angles greater than 90° but these angles also "deserve" to have their owns sines and cosines.

STEP 3:

Go on