[ Current Projects | Hot List | Personal Interests | Contact Information | Encryption-Decryption software | Karnaugh map generalization | Energy accumulation | Energy Density | Arithmetic engine | Astronomy Coordinates | Curriculum Vitae | Home Page ].
Operational and polynomial expansions
Conversions and optimizations
Developed Karnaugh map for n variables
For binary values function of n variables f(x1x2… xn) , the operational expansion is :
![]()
If complemented x is replaced by 0 and x by 1 then the figuring of the function expansion is:
![]()
With a* is of binary value.
The polynomial expansion is:
![]()
Such that x1=x and x0=1 and b* is of binary value.
According to the values of a0, a1 … or b0, b1 … the function variable number and expansion terms may be optimized using the Karnaugh map (not the traditional 4 variables but the new n-variables map).
The n-variables map can be used with both, operational and polynomial expansions and can easily find the coefficients of the other expansion using a certain map of 2n-1 dimensions or using folding (folding here is applied for n-variables).
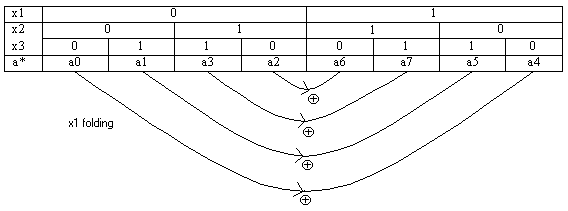
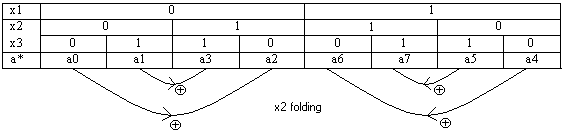
The technique is: (e.g. n=3)
| x1 |
0 |
1 |
||||||
| x2 |
0 |
1 |
1 |
0 |
||||
| x3 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
| a* |
a0 |
a1 |
a3 |
a2 |
a6 |
a7 |
a5 |
a4 |
| b* |
b0 |
b1 |
b3 |
b2 |
b6 |
b7 |
b5 |
b4 |
The optimization of the expansion is done by reducing the number of terms in the expansion such that the consecutive buddy terms of equal value (either 0 or 1) are reduced to the highest variables, for example if a1=a2=a3 then the buddy block is a1, a3 only and it’s two terms are reduced to the highest variables.
Also for example if a0=a1=a3=a2 then the reduction is to the variable x1
If a2=a6, no reduction is obtained since the two terms are not buddy.
The same is when x0 or x1 are the correspondence of 0 and 1 in the map.
Obtaining the coefficients from the following map does the conversion from operational to polynomial:
|
a0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
a1 |
1 |
1 |
1 |
1 |
||||
|
a2 |
1 |
1 |
1 |
1 |
||||
|
a3 |
1 |
1 |
||||||
|
a4 |
1 |
1 |
1 |
1 |
||||
|
a5 |
1 |
1 |
||||||
|
a6 |
1 |
1 |
||||||
|
a7 |
1 |
|||||||
| b0 |
b1 |
b2 |
b3 |
b4 |
b5 |
b6 |
b7 |
The above map obtains polynomial coefficients (b’s) from the operational such that 1 means the term exists in the XOR expansion of b.
The folding technique is very simple and can be easily computerized to any number of variables, the folding is done by XOR masking of the map around it’s middle as follows: