
Página Principal Noções
Básicas Algoritmos
Genéticos Redes Neurais
Multiagentes
Cognição Software
Artigos Tutoriais
Links Quem
sou eu

Neste ponto existiria uma extensa área para transcrever, mas será, por praticidade, limitada a explicar superficialmente as teorias de Darwin, deixando para pesquisa individual (se necessário for), a consulta aos trabalhos de Mendel, Lamark e DeVries, entre outros.
![]()
AS IDÉIAS EVOLUCIONISTAS DE DARWIN (DARWINISMO)
Em meados do século XIX, Charles Darwin (1809-1882) revolucionou todo o pensamento acerca da evolução da vida e de nossas origens, provocando a maior discussão que já houve à respeito de uma teoria científica. Em seus dois livros - Sobre a Origem das Espécies por Meio da Seleção Natural (1859), e A Descendência do Homem e Seleção em Relação ao Sexo (1871) - Darwin defendia que o homem, tal qual os outros seres vivos, é resultado da evolução .
Em seus estudos, Darwin concluiu que nem todos os organismos que nascem, sobrevivem ou (o que é mais importante) reproduzem-se. Os indivíduos com mais oportunidades de sobrevivência seriam aqueles com características mais apropriadas para enfrentar as condições ambientais. Esses indivíduos teriam maior probabilidade de reproduzir-se e deixar descendentes. Nessas condições as variações favoráveis tenderiam a ser preservadas e as desfavoráveis, destruídas.
É um lento e constante processo de seleção ao longo das gerações, através do qual as espécies podem se diversificar, tornando-se mais adaptadas ao ambiente em que vivem. Nascia assim o conceito de Seleção Natural, a grande contribuição de Darwin à teoria da evolução.
O mecanismo de evolução proposto por Darwin pode ser resumido em seis etapas:
| Os indivíduos de uma mesma espécie mostram muitas variações na forma e na fisiologia; | |
| Boa parte dessas variações é transmitida aos descendentes; | |
| Se todos os indivíduos de uma espécie se reproduzissem, as populações cresceriam exponencialmente; | |
| Como os recursos naturais são limitados, os indivíduos de uma população lutam por sua sobrevivência e de sua prole; | |
| Portanto, somente alguns (os mais aptos), sobrevivem e deixam descendentes. A sobrevivência e a reprodução diferencial dependem das características desses indivíduos que, por serem hereditárias, serão transmitidas aos seus filhos; | |
| Através dessa seleção natural, as espécies serão representadas por indivíduos cada vez mais adaptados. |
A explicação de Darwin para o exemplo do aumento do pescoço das girafas é, essencialmente, muito simples: em uma população inicial de girafas, alguns indivíduos possuíam pescoços mais altos do que os outros. Essas girafas passaram a ter maiores chances de alimentação (consequentemente maior chance de sobreviver) a partir do instante em que ocorreu escassez de alimento próximo ao solo e foram, então, selecionadas positivamente, enquanto as de pescoço mais curto tendiam a se extinguir. O processo se repetiu ao longo das gerações e, com isso, a freqüência de animais de pescoço comprido aumentou de maneira gradativa.
O principal problema da teoria darwiniana foi a falta de uma teoria satisfatória que explicasse a origem e a transmissão das variações.
Darwin não conseguiu responder adequadamente estas críticas e, somente com a posterior redescoberta das Leis de Mendel e das Mutações, foi que esses problemas puderam ser resolvidos. Apesar disso, não há dúvida de que a teoria moderna da evolução deve mais a Darwin do que a qualquer outro cientista, e seu conceito de seleção natural continua válido até hoje.
![]()
A idéia básica de seleção natural foi apresentada por Charles Darwin e representa uma das maiores conquistas no campo científico, particularmente, na ciência biológica. É o mecanismo de seleção que impõe uma certa ordem ao processo de evolução.
A primeira parte do processo, se caracteriza pela obtenção de variedade genética e é realizada ao acaso. Já a Segunda parte, composta pela seleção, é em certo grau determinada pelos fatores ecológicos do ambiente.
Através da seleção natural, a freqüência de um gene vantajoso aumenta gradativamente na população. A vantagem conferida pelo gene pode se refletir em um maior tempo de sobrevivência do indivíduo, aumentando assim a quantidade de filhos que ele produz. Pode implicar também uma fertilidade maior do indivíduo que, mesmo sobrevivendo menos tempo, poderá deixar um número maior de filhos que seu competidor. Finalmente, o gene poderá aumentar a sua freqüência se ele fornecer ao indivíduo maior capacidade de proteção. Assim, mesmo se ele tiver menos filhos, suas chances de atingir a época de reprodução serão maiores.
Um exemplo clássico de seleção natural é o caso das mariposas de Manchester na Inglaterra, ocorrido durante a Revolução Industrial.
Antes da industrialização, existia na cidade de Manchester uma população de mariposas de asas brancas, tendo essa população alguns mutantes de asas negras. Os pássaros (principais predadores) atacavam principalmente a espécie mutante, pois as mariposas de asas brancas se camuflavam facilmente nos troncos das arvores revestidos de liquens brancos.
Contudo, com a industrialização, a fuligem ocasionou a morte dos liquens, deixando os troncos escuros, expostos. Dessa forma, as mariposas escuras passaram a ter a vantagem da camuflagem, obtendo assim maior probabilidade de sobrevivência e aumentando a sua descendência. As mariposas brancas, ao contrário, por terem se tornado mais visíveis sobre os troncos escuros, passaram a ser o alvo principal dos seus predadores, tendo uma estimativa de vida mais curta e, consequentemente, deixando um número menor de descendentes.
Com o passar das gerações, foi aumentando gradativamente a freqüência de mariposas negras, até representarem praticamente toda a população (cerca de 90%), adaptada, portanto, ao novo ambiente.
![]()
A primeira tentativa de representação, por meio de um modelo matemático, da teoria de Darwin, surgiu com o livro The Genetic Theory of Natural Selection, escrito pelo biólogo evolucionista R. A. Fisher. A evolução era, tal como a aprendizagem, uma forma de adaptação, diferindo apenas na escala de tempo. Em vez de ser o processo de uma vida, era o processo de gerações. Como era feita em paralelo por um conjunto de organismos, tornavase mais poderosa que a aprendizagem.
A seguir, John Holland dedicouse ao estudo de processos naturais adaptáveis, tendo inventado os AG’s em meados da década de 60. Ele desenvolveu os AG’s em conjunto com seus alunos e colegas da Universidade de Michigan nos anos 60 e 70, com o objetivo de estudar formalmente o fenômeno da adaptação como ocorre na natureza, e desenvolver modelos em que os mecanismos da adaptação natural pudessem ser importados para os sistemas computacionais.
Como resultado do seu trabalho, em 1975, Holland edita Adaptation in Natural and Artificial Systems [HOL75] e, em 1989, David Goldberg edita Genetic Algorithms in Search, Optimization and Machine Learning [GOL89], hoje considerados os livros mais importantes sobre AG’s.
![]()
Os AG’s são técnicas de busca baseadas nas Teorias da Evolução, nos quais as variáveis são representadas como genes em um cromossomo (indivíduo). Combinam a sobrevivência dos mais aptos com a troca de informação de uma forma estruturada, mas aleatória. O AG apresenta um grupo de soluções candidatas (População) na região de soluções. Por seleção natural e operadores genéticos, mutação e cruzamento, os cromossomos com melhor aptidão são encontrados. A seleção natural garante que os cromossomos mais aptos gerem descendentes nas populações futuras. Usando um operador de cruzamento, o AG combina genes de dois cromossomos pais previamente selecionados para formar dois novos cromossomos, os quais têm uma grande possibilidade de serem mais aptos que os seus genitores.
Holland acreditava que a incorporação das características naturais de evolução em um computador poderia produzir uma técnica para solucionar problemas da mesma maneira como funcionam na natureza os processos de seleção e adaptação. A forma de codificação dos cromossomos biológicos ainda não é totalmente compreendida pela comunidade científica, apesar dos enormes avanços conseguidos até os dias de hoje, mas existem algumas características gerais da teoria que são aceitas, tais como [DAV91]:
Evolução;
Seleção natural;
Reprodução;
Ausência de memória.
Os Algoritmos Genéticos ocupam lugar de destaque entre os paradigmas da CE devido a uma série de razões dentre as quais [GUI98] [SER96]:
| Apresentam-se como o paradigma mais completo da CE visto que englobam de forma simples e natural todos os conceitos nela contidos; | |
| Apresentam resultados bastante aceitáveis, com relação à precisão e recursos empregados (fáceis de implantar em computadores domésticos de porte médio), para uma ampla gama de problemas de difícil resolução por outros métodos; | |
| São muito flexíveis, aceitam sem grandes dificuldades uma infinidade de alterações na sua implementação e permitem fácil hibridação (vantagem importante no caso de aprendizagem) inclusive com técnicas não relacionadas à CE; | |
| Em relação aos outros paradigmas da CE, são os que exigem menor conhecimento específico do problema em questão para o seu funcionamento , o que os torna altamente versáteis e, além disso, agregam conhecimento específico com pouco esforço; | |
| São o paradigma mais usado dentro da CE e, junto com as Redes Neurais, os mais usados de toda a Computação Natural. |
Na prática, nós podemos implementar facilmente um AG com o simples uso de strings de bits ou caracteres para representar os cromossomos e, com simples operações de manipulação de bits podemos implementar cruzamento, mutação e outros operadores genéticos. Na figura 1, podemos ver a simplicidade de representação de um cromossomo composto por dez genes, por meio de uma string de valores binários.

Figura 1 – Exemplo de representação de um cromossomo de genes binários.
O pseudocódigo de um AG básico é mostrado na figura 2. Nele podemos ver que os AG’s começam com uma população de n estruturas aleatórias (indivíduos), onde cada estrutura codifica uma solução do problema. O desempenho de cada indivíduo é avaliado com base numa função de avaliação de aptidão. Os melhores tenderão a ser os progenitores da geração seguinte, melhorando, de geração para geração, através da troca de informação.
| Algorithm AG is | |||
| t := 0; | // determinar um tempo inicial | ||
| InitPop P(t); | // iniciar uma população de indivíduos randômica | ||
| eval P(t); | // avaliar aptidão dos indivíduos da população | ||
| while not done do | // testar critérios (tempo, aptidão, etc.) | ||
| t := t + 1; | // incrementar o contador de tempo | ||
| P' := SelectPar P(t); | // selecionar os pares para cruzamento | ||
| Recombine P' (t); | // realizar cruzamento dos pares selecionados | ||
| Mutate P' (t); | // perturbar o grupo gerado pelo cruzamento | ||
| Evaluate P' (t); | // avaliar as novas aptidões | ||
| P := Survice P, P'(t); | // selecionar os sobreviventes | ||
| od | |||
| End AG. | |||
Figura 2 – Pseudocódigo básico de um Algoritmo Genético
Pelo que foi apresentado até o momento, nota-se que a principal inovação dos AG’s, no que se refere aos métodos de busca, é a implementação de um mecanismo de seleção de soluções no qual, a curto prazo os melhores têm maior probabilidade de sobreviver e, a longo prazo, os melhores têm maior probabilidade de ter descendência. Desta forma, o mecanismo de seleção se divide em dois segmentos: o primeiro escolhe os elementos que vão participar da transformação (operador de seleção) e o outro escolhe os elementos que vão sobreviver (operador de substituição)
Cabe ainda destacar que os AG’s são métodos de busca [GUI98]:
| Cega: não tem conhecimento específico do problema a ser resolvido, tendo como guia apenas a função objetivo; | |
| Codificada: não trabalham diretamente com o domínio do problema e sim com representações dos seus elementos; | |
| Múltipla: executa busca simultânea em um conjunto de candidatos; | |
|
Estocástica: aleatória. Combinam em proporção variável regras probabilísticas e determinísticas. Esse conceito refere tanto as fases de seleção como as de transformação. |
A vantagem principal dos AG’s ao trabalharem com o conceito de população, ao contrário de muitos outros métodos que trabalham com um só ponto, é que eles encontram segurança na quantidade. Tendo uma população de pontos bem adaptados, é reduzida a possibilidade de alcançar um falso ótimo. Os AG’s conseguem grande parte de sua amplitude simplesmente ignorando informação que não constitua parte do objetivo, enquanto outros métodos se apoiam fortemente nesse tipo de informação e, em problemas nos quais a informação necessária não está disponível ou se apresenta de difícil acesso, estes outros métodos falham. Em suma, os AG’s podem ser aplicados praticamente em qualquer problema.
Apesar de aleatórios, eles não são caminhadas aleatórias não direcionadas, ou seja, buscas totalmente sem rumo, pois exploram informações históricas para encontrar novos pontos de busca onde são esperados melhores desempenhos. Isto é feito através de processos iterativos, onde cada iteração é chamada de geração.
![]()
É importante também, analisar de que maneira alguns parâmetros influem no comportamento dos Algoritmos Genéticos, para que se possa estabelecê-los conforme as necessidades do problema e dos recursos disponíveis. Serão listados a seguir alguns Parâmetros Genéticos utilizados:
Tamanho da População: O tamanho da população determina o número de cromossomos na população, afetando diretamente o desempenho global e a eficiência dos AG’s. Com uma população pequena o desempenho pode cair, pois deste modo a população fornece uma pequena cobertura do espaço de busca do problema. Uma grande população geralmente fornece uma cobertura representativa do domínio do problema, além de prevenir convergências prematuras para soluções locais ao invés de globais. No entanto, para se trabalhar com grandes populações, são necessários maiores recursos computacionais, ou que o algoritmo trabalhe por um período de tempo muito maior.
Taxa de Cruzamento: Quanto maior for esta taxa, mais rapidamente novas estruturas serão introduzidas na população. Mas se esta for muito alta, a maior parte da população será substituída, e pode ocorrer perda de estruturas de alta aptidão. Com um valor baixo, o algoritmo pode tornar-se muito lento.
Tipo de Cruzamento: O tipo de cruzamento a ser utilizado determina a forma como se procederá a troca de segmentos de informação entre os "casais" de cromossomos selecionados para cruzamento. Mais adiante serão explanados alguns tipos de cruzamento utilizados mas, deve-se levar em conta que existem muitas outras escolhas disponíveis para usuários de AG’s. O ideal, seria testar diversos tipos de cruzamento em conjunto com as outras configurações do AG em uso para verificar qual apresenta um melhor resultado.
Taxa de Mutação: Determina a probabilidade em que uma mutação ocorrerá. Mutação é utilizada para dar nova informação para a população e também para prevenir que a população se sature com cromossomos semelhantes (Convergência Prematura). Uma baixa taxa de mutação previne que uma dada posição fique estagnada em um valor, além de possibilitar que se chegue em qualquer ponto do espaço de busca. Com uma taxa muito alta a busca se torna essencialmente aleatória além de aumentar muito a possibilidade de que uma boa solução seja destruída. A melhor Taxa de Mutação é dependente da aplicação mas, para a maioria dos casos é entre 0,001 e 0,1.
ESTRUTURA E COMPONENTES BÁSICOS
Como não há uma definição rigorosa para "Algoritmo Genético" a qual seja aceita por todos os componentes da comunidade da computação evolucionária, podemos dizer que a maioria dos métodos denominados "AG’s" têm pelo menos os seguintes elementos em comum:
Uma população de cromossomos;
Seleção de acordo com a aptidão;
Cruzamento (crossover) para gerar novas populações;
Mutação aleatória para produzir novos indivíduos.
Os cromossomos componentes da população de um AG, assumem tipicamente a forma de strings binárias. Cada posição dentro dessa string tem dois alelos possíveis: 0 e 1. Cada cromossomo pode ser visto como um ponto no espaço de busca das soluções candidatas. O AG processa populações de cromossomos, efetuando substituições sucessivas de uma população por outra. Os AG’s requerem uma função de aptidão que atribua um valor (valor de aptidão ou fitness) para cada cromossomo da população atual. O valor de aptidão de cada cromossomo depende de quão bem este cromossomo resolve o problema dado.
Um esquema gráfico da estrutura de um AG básico seria como o apresentado na figura 3.

Figura 3 – Estrutura básica de um AG.
Como pode ser visto, uma população Popt que consta de n membros é submetida a um processo de seleção onde será gerada uma população auxiliar PopAuxt de n criadores. Dessa população auxiliar será extraído um subgrupo de indivíduos denominados progenitores que são os que efetivamente vão se reproduzir. Fazendo uso dos operadores genéticos, os progenitores passarão por uma série de transformações na fase de reprodução, por meio das quais serão gerados os indivíduos componentes da Descendência. Para formar a nova população Pop[t+1], devem ser selecionados n sobreviventes dos n+s da população auxiliar e da descendência, o que é feito na fase de Substituição. A fase de Seleção é realizada em duas etapas (retângulo mais escuro) com finalidade de emular as duas vertentes do princípio de seleção natural: seleção de criadores ou Seleção e seleção de sobreviventes para a próxima geração ou Substituição.
![]()
MÉTODOS E CRITÉRIOS PARA IMPLANTAÇÃO DE UM AG
Para implantar um AG, necessita-se definir de forma correta os seguintes métodos e critérios [SER96]:
Critério de codificação: tendo em vista que os AG’s trabalham com manipulação de strings de determinados alfabetos (representação), deve-se especificar a codificação com a qual se faz corresponder cada ponto do domínio do problema com um Gene ou conjunto de Genes do Cromossomo.
Critério de tratamento dos indivíduos não factíveis: nem sempre é possível estabelecer uma correspondência ponto-a-ponto entre o domínio do problema e o conjunto de strings binárias (ou de outro alfabeto utilizado) usadas para resolvê-lo. Como conseqüência, nem todas as strings (indivíduos) codificam indivíduos válidos do espaço de busca e devem ser habilitados procedimentos úteis para distingui-las.
Critério de inicialização: refere-se a como deve ser construída a população inicial com a qual se inicializará o AG.
Critério de parada: devem ser determinadas as condições nas quais se considera que o AG encontrou uma solução aceitável ou tenha fracassado no processo de busca e não faça sentido continuar.
Funções de avaliação e aptidão: deve ser determinada a função de avaliação mais apropriada para o problema, assim como a função de aptidão que utilizará o AG para resolvê-lo.
Operadores Genéticos: denominação dada aos operadores utilizados para levar a cabo a reprodução. Todo AG faz uso de pelo menos três Operadores Genéticos (levando em conta o AG básico): seleção, cruzamento e mutação. Fique claro que estes não são os únicos possíveis e além de tudo admitem variações.
Critérios de Seleção: a seleção deve dirigir o processo de busca em favor dos indivíduos mais aptos. Isto pode ser feito de varias maneiras como, por exemplo, por amostragem direta, por amostragem aleatória simples ou por amostragem estocástica, como poderá ser visto mais adiante.
Critério de Substituição: os critérios com que se selecionam os criadores não necessariamente têm que ser os mesmos usados para selecionar os sobreviventes, logo a necessidade de especificá-los separadamente. Alguns exemplos são:
Substituição Imediata: os s descendentes substituem seus progenitores
Substituição por fator cheio: os s descendentes substituem aqueles membros da população mais parecidos com eles
Substituição por inserção: são selecionados para serem eliminados s membros da população de criadores (geralmente os s piores), os quais serão substituídos pelos descendentes.
Substituição por Inclusão: os s descendentes são somados aos n progenitores em uma única população e nesta, são selecionados os n melhores.
Parâmetros de Funcionamento: um AG precisa que lhe proporcionem certos parâmetros de funcionamento (tamanho da população, probabilidades de aplicação dos Operadores Genéticos, precisão da codificação, ...)
A seleção de um ou outro método ou critério acima depende não apenas do tipo de problema a ser resolvido, mas também de que não sejam violados certos requisitos imprescindíveis ao bom funcionamento do AG.
![]()
A literatura sobre AG’s descreve uma vasta gama de aplicações nas quais estas técnicas obtiveram pleno sucesso, mas existem também inúmeros casos onde a performance dos AG’s não conseguiu obter bons resultados. Então, dado um determinado problema a ser resolvido, como podemos saber se o AG é um bom método para solucioná-lo?
Em geral, os AG’s têm sido mais usados para solução de funções de otimização, nas quais eles têm se mostrado bastante eficientes e confiáveis. Mas, como é de se esperar, nem todos os problemas podem ter resultados satisfatórios ou mesmo ser representados adequadamente para o uso de técnicas de AG. A recomendação geral é levar em conta as seguintes características relativas ao problema, antes de tentar o uso das referidas técnicas [GOL89]:
| O espaço de busca (possíveis soluções) do problema em questão deve estar delimitado dentro de uma certa faixa de valores. | |
|
Deve ser possível definir uma função de aptidão (fitness) que nos indique quão boa ou ruim é uma determinada resposta. |
|
| As soluções devem poder ser codificadas de uma maneira que resulte relativamente fácil a sua implementação no computador. |
![]()
MECANISMOS DE AMOSTRAGEM DE POPULAÇÕES
Após decidir como será realizada a codificação de um AG (forma de representação do problema com números binários ou outro alfabeto), o passo seguinte é decidir como o AG procederá para seleção dos indivíduos (cromossomos), ou seja, como escolher os indivíduos na população que criarão os descendentes para a próxima geração.
Os mecanismos de amostragem são bastante variados, sendo que, entre eles, se destacam três grupos principais segundo o grau de influência da aleatoriedade no processo:
Amostragem direta: seleção de um subconjunto de indivíduos da população mediante um critério fixo, no estilo de "os n melhores", "os n piores", "a dedo", etc...
Amostragem aleatória simples ou equiprovável: é determinada a mesma probabilidade para todos os elementos da população, de serem selecionados para a amostra.
Amostragem estocástica: são atribuídas probabilidades de seleção ou pontuações aos elementos da população com base na sua função de aptidão (fitness).
Existem muitos mecanismos de amostragem estocástica, de acordo com a sua aplicação, dos quais explanaremos apenas uns poucos a seguir:
Por sorteio: as pontuações são consideradas estritamente como probabilidades de seleção para formar a amostra, a qual é constituída realizando n ensaios de uma variável aleatória com dita distribuição de probabilidades. Para ilustrar, levemos em conta a existência de uma população de 4 indivíduos
, e digamos que o resultado da função de aptidão de cada indivíduo seja, respectivamente
,
,
,
.
Os passos seguintes seriam:1) Calcular as pontuações acumuladas da seguinte forma:

2) Gerar um número aleatório simples
, o qual a termo de exemplo consideraremos
.
3) Por meio do número gerado aleatoriamente, eleger o indivíduo que se encaixe na regra:

No nosso exemplo, o indivíduo selecionado seria o
, pois:
ou seja,
Para realizar a amostragem por sorteio de
indivíduos, devemos apenas modificar os últimos dois passos da seguinte forma:
2) Gerar
números aleatórios simples
.
3) Para cada
se escolhe o indivíduo
que verifique

Por restos: a cada indivíduo
é atribuído diretamente
locais na amostra. Freqüentemente os indivíduos repartem os locais vagos em função das suas pontuações. A distribuição costuma ser por sorteio (ver item anterior) e então se diz "amostragem estocástica por restos". Continuando com o exemplo proposto, a
é atribuído um local na amostra; o indivíduo que ocupará o outro local é selecionado por sorteio, pela geração de um número aleatório simples
e se compara o seu valor com as pontuações acumuladas
, seguindo a mesma regra anterior (
).
Universal ou por roleta: inicialmente proposto por Goldberg [GOL89]. É um método bastante simples que consiste em criar uma roleta na qual cada cromossomo possui um segmento proporcional à sua aptidão. Suponhamos uma população de 6 cromossomos cuja aptidão é dada por uma função qualquer (neste caso é simplesmente a conversão de binário para decimal) conforme mostrado na tabela 1.
Tabela 1 – Valores de exemplo para ilustrar seleção por roleta.
|
Cromossomo nº |
String |
Aptidão |
% do total |
|
1 |
0101101 |
45 |
13,2 |
|
2 |
1011001 |
89 |
26,2 |
|
3 |
1111101 |
125 |
36,7 |
|
4 |
0010101 |
21 |
6,1 |
|
5 |
0110100 |
52 |
15,2 |
|
6 |
0001001 |
9 |
2,6 |
|
Total |
341 |
100,0 |
Com os valores percentuais constantes na quarta coluna da tabela 1, iremos elaborar a roleta constante da figura 4. Esta roleta irá ser girada 6 vezes para efetuar a seleção da população auxiliar (amostra) levando em conta que, os indivíduos com maior área na roleta tem, consequentemente, maiores chances de serem selecionados mais vezes que os indivíduos menos aptos.
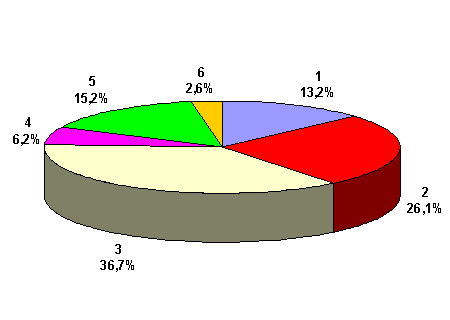
Figura 4 – Representação gráfica da roleta.
Por torneio: o processo usado neste método é extremamente simples. Cada elemento da amostra e selecionado elegendo o melhor indivíduo de um conjunto deelementos tomados aleatoriamente na população base; isto é repetido o número de vezes necessárias para completar a amostra. O valor do parâmetro
costuma ser um valor inteiro pequeno em relação ao tamanho total da população base, sendo em geral 2 ou 3.
São os operadores genéticos que transformam a população através de sucessivas gerações, estendendo a busca até chegar a um resultado satisfatório. Um algoritmo genético padrão evolui, em suas sucessivas gerações, mediante o uso de três operadores básicos:
Seleção : realiza o processo de adaptabilidade e sobrevivência;
Cruzamento : representa o acasalamento entre os indivíduos;
Mutação : introduz modificações aleatórias.
Seleção:
A idéia principal do operador de seleção em um algoritmo genético, é oferecer aos melhores indivíduos da população corrente, preferência para o processo de reprodução, permitindo que estes indivíduos possam passar as suas características às próximas gerações. Isto funciona como na natureza, onde os indivíduos altamente adaptados ao seu ambiente possuem naturalmente mais oportunidades para reproduzir do que aqueles indivíduos considerados mais fracos [SCH98].
Cruzamento:
Poderia ser dito que a principal característica de distinção do AG em relação as outras técnicas é o uso do cruzamento [MIT96].
O operador Cruzamento é utilizado após o de seleção. Esta fase é marcada pela troca de segmentos entre "casais" de cromossomos selecionados para dar origem a novos indivíduos que formarão a população da próxima geração.
A idéia central do cruzamento é a propagação das características dos indivíduos mais aptos da população por meio de troca de segmentos informações entre os mesmos o que dará origem a novos indivíduos.
As duas formas mais comuns de reprodução sexual em AG’s são de um ponto de cruzamento e de dois pontos de cruzamento.
Um ponto de cruzamento (single-point crossover): o ponto de quebra do cromossomo é escolhido de forma aleatória sobre a longitude da string que o representa, e é a partir desse ponto que se realiza a troca de material cromossômico entre os dois indivíduos, como é representado na figura 5, na qual a termo de representação foi escolhido o ponto de cruzamento 4.
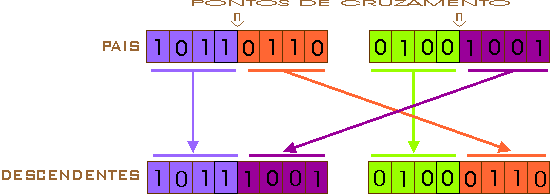
Figura 5 – Esquema gráfico do cruzamento de um ponto.
Dois pontos de cruzamento (two-point crossover): procede-se de maneira similar ao cruzamento de um ponto, mas a troca de segmentos do gene ocorre como mostrado na figura 6, na qual a termo de representação foram escolhidos os pontos 2 e 6:
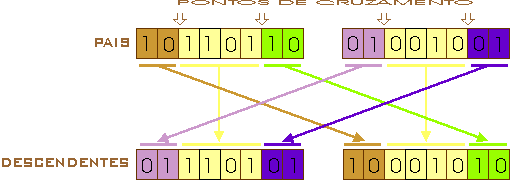
Figura 6 – Esquema gráfico do cruzamento de dois pontos.
Cruzamento Uniforme (uniform crossover): É radicalmente diferente do cruzamento de um ponto. Cada gene do descendente é criado copiando o gene correspondente de um dos pais, escolhido de acordo com uma máscara de cruzamento gerada aleatoriamente. Onde houver 1 na máscara de cruzamento, o gene correspondente será copiado do primeiro pai e, onde houver 0 será copiado do segundo. O processo é repetido com os pais trocados para produzir o segundo descendente. Uma nova máscara de cruzamento é criada para cada par de pais. O número de pontos de troca de informação não é fixo mas em geral é usado
(onde
é o comprimento do cromossomo). A figura 7 demonstra graficamente o processo.

Figura 7 – Esquema gráfico do cruzamento uniforme.
Mutação:
A
mutação é geralmente vista como um operador de "background",
responsável pela a introdução e manutenção
da diversidade genética na população [HOL75]. Ela trabalha
alterando arbitrariamente um ou mais componentes de uma estrutura escolhida
entre a descendência, logo após o cruzamento, fornecendo dessa
forma meios para a introdução de novos elementos na população.
Assim, a mutação assegura que a probabilidade de se chegar a qualquer
ponto do espaço de busca nuca será zero. O operador de mutação
é aplicado aos indivíduos com uma probabilidade dada pela taxa
de mutação ![]() . Como foi
visto no item Parâmetros Genéticos, geralmente se utiliza uma taxa
de mutação pequena, justamente por ser um operador genético
secundário. A figura 8 ilustra o processo de mutação em
um indivíduo da descendência.
. Como foi
visto no item Parâmetros Genéticos, geralmente se utiliza uma taxa
de mutação pequena, justamente por ser um operador genético
secundário. A figura 8 ilustra o processo de mutação em
um indivíduo da descendência.

Figura 8 – Esquema gráfico de ocorrência de Mutação.
A
ocorrência de mutação em determinado gene é dada
pela taxa de mutação a qual usualmente, possui um valor pequeno
(![]() ) sendo alguns dos valores mais
comumente usados
) sendo alguns dos valores mais
comumente usados ![]() e
e ![]() .
Nas últimas pesquisas tem se constatado que a performance do AG tende
a decair em populações de tamanho relativamente grande (
.
Nas últimas pesquisas tem se constatado que a performance do AG tende
a decair em populações de tamanho relativamente grande (![]() )
usando grande probabilidade de mutação (
)
usando grande probabilidade de mutação (![]() )
e em populações de pequeno tamanho (
)
e em populações de pequeno tamanho (![]() )
combinadas com pequena probabilidade de mutação (
)
combinadas com pequena probabilidade de mutação (![]() )
[BAC96].
)
[BAC96].
Como
foi visto, a mutação em geral se restringe a inversão do
valor de certos bits, determinada aleatoriamente com base em uma taxa de probabilidade.
Assim temos, para melhor compreensão, que para cada indivíduo
de comprimento ![]() aplicando o operador
de mutação passaremos a ter um indivíduo
aplicando o operador
de mutação passaremos a ter um indivíduo ![]() ,
tal que
,
tal que

onde
![]() representa o bit, do indivíduo,
que está sendo avaliado para mutação e
representa o bit, do indivíduo,
que está sendo avaliado para mutação e ![]() é um número aleatório (
é um número aleatório (![]() )
atribuído a ele para comparação com a taxa de mutação
)
atribuído a ele para comparação com a taxa de mutação
![]() . Dessa forma, aplicando a regra
acima, será obtida a inversão de bit (no caso de indivíduos
compostos por strings binárias) sempre que o valor de
. Dessa forma, aplicando a regra
acima, será obtida a inversão de bit (no caso de indivíduos
compostos por strings binárias) sempre que o valor de ![]() atribuído a
atribuído a ![]() for menor ou
igual a
for menor ou
igual a ![]() ; caso contrário o
bit permanecerá inalterado.
; caso contrário o
bit permanecerá inalterado.
O PROBLEMA DA DIVERSIDADE NOS AG’S
Um ponto fundamental para o bom funcionamento de um AG é a existência de diversidade entre os indivíduos. Ou seja, deve existir um certo grau de diversidade entre as aptidões dos indivíduos que compõe o conjunto de possíveis soluções pois, do contrário, com um conjunto de indivíduos muito semelhantes, o operador de cruzamento perde em muito a capacidade de troca de informações úteis entre os indivíduos da população o que faz a busca em certos casos progredir muito lentamente ou praticamente estacionar.
A necessidade de ter controlada a diversidade dentro de uma determinada população, tem, como um dos seus maiores obstáculos, a necessidade de populações finitas e não muito grandes. Caso contrário, poderia tornar não aplicável na prática, uma técnica de AG, visto que, controlar uma população absurdamente grande, a qual tenha cálculos muito complexos para determinar a aptidão, poderia ocasionar um esforço computacional muito grande. Devemos lembrar que o esforço computacional será relativo ao tipo de aplicação pois, por exemplo, se tratando do controle de um robô móvel que dependa de respostas em tempo real para desvio de obstáculos, um atraso de 1 segundo na tomada de uma decisão pode ser catastrófico.
Em suma, para que a seleção seja efetiva, a população deve conter, a todo instante, uma certa variedade de aptidões, o que, como foi visto com relação ao tamanho da população, implica também em não ter uma disparidade muito grande de aptidões, pois costuma afetar negativamente a diversidade da população. Para melhor entendimento, devemos conhecer também dois conceitos intrinsecamente ligados com a diversidade que são a Convergência e a Pressão Seletiva, os quais são explicados a seguir:
Convergência e Elitismo
Levando em conta, a termo de exemplo, um AGS de população finita, a convergência ocorre quando um ou mais indivíduos assumem um valor de aptidão muito superior aos demais (superindivíduo - fato que ocorre mais freqüentemente no início do processo, quando um determinado indivíduo pode ser privilegiado em relação ao resto da população que pode apresentar aptidões medíocres), tendo assim maiores chances de sobreviver e reproduzir, ao ponto de poder até mesmo, tomar conta da população com sua descendência. Este fenômeno é chamado de evolução em avalanche, ou seja, por serem privilegiados os superindivíduos em uma população finita, a diversidade diminui e isso faz com que na geração seguinte se favoreçam ainda mais os indivíduos mais aptos até o momento que eles dominam por completo a população, o que termina acarretando uma convergência prematura do AG geralmente em direção a um subótimo.
O único momento em que este tipo de fenômeno é aceitável e até mesmo desejável, é nas fases tardias da evolução ou seja, quando o AG já tenha localizado corretamente a solução ótima.
O método mais utilizado para melhorar a convergência dos AG’s é o Elitismo. Ele foi primeiramente introduzido por Kenneth De Jong (1975) e é uma adição aos vários métodos de seleção que força os AG’s a reter um certo número de "melhores" indivíduos em cada geração. Tais indivíduos podem ser perdidos se eles não forem selecionados para reprodução ou se eles forem destruídos por cruzamento ou mutação. Muitos pesquisadores tem encontrado no elitismo vantagens significativas para a performance dos AG’s [MIT96].
O Elitismo consiste basicamente de realizar a etapa de seleção em duas partes:
membros restantes da população inicial.1 - Se seleciona uma elite de
membros entre os melhores da população inicial, os quais serão incorporados diretamente à população final, sem passar pela população auxiliar.
2 - A população auxiliar é selecionada entre os

Em
geral, a elite tem um tamanho reduzido (1 ou 2 para ![]() )
e a sua amostragem pode ser direta (os
)
e a sua amostragem pode ser direta (os ![]() melhores) ou por sorteio (os
melhores) ou por sorteio (os ![]() melhores
entre os
melhores
entre os ![]() melhores da população).
O esquema gráfico do Elitismo pode ser visualizado na figura 9.
melhores da população).
O esquema gráfico do Elitismo pode ser visualizado na figura 9.
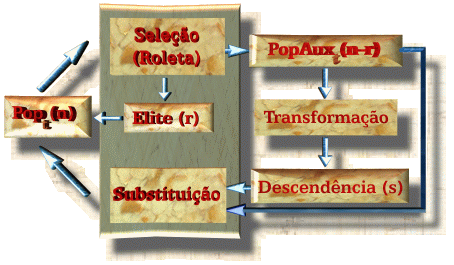
Figura 9 – Esquema gráfico do processo de Elitismo.
Pressão Seletiva
Para controlar a diversidade na população, deve-se ter um controle sobre o mecanismo de determinação de probabilidades de sobrevivência pois, como foi visto, quanto mais se favoreça os indivíduos mais aptos, menor será a variedade da população podendo ocorrer uma convergência prematura para um ótimo local. Por outro lado, se não há um favorecimento especial aos indivíduos mais aptos, haverá com certeza maior diversidade na população mas tornará o AG menos eficaz.
O controle do mecanismo de determinação de probabilidades de sobrevivência dos indivíduos mais aptos é denominado pressão seletiva cuja aplicação ideal seria: menor pressão seletiva no início do processo, favorecendo a diversidade e maior pressão seletiva na etapa final do processo para favorecer a convergência para um ótimo global.
Uma forma pela qual podemos quantificar o conceito de pressão seletiva em um valor numérico seria:

Onde:
![]() =
Pressão Seletiva da geração
=
Pressão Seletiva da geração ![]()
![]() = Maior valor de aptidão da geração
= Maior valor de aptidão da geração ![]()
![]() = Aptidão média da geração
= Aptidão média da geração ![]()
Para
manter a diversidade dos indivíduos relativamente uniforme, recomenda-se
trabalhar com valores de ![]() próximos
de 1.5, visto que valores maiores ocasionariam o surgimento de superindivíduos
e valores menores estagnariam a busca. Logicamente, o valor mínimo de
Pressão Seletiva é 1, o qual corresponde a situação
na qual todos os indivíduos são iguais (diversidade nula).
próximos
de 1.5, visto que valores maiores ocasionariam o surgimento de superindivíduos
e valores menores estagnariam a busca. Logicamente, o valor mínimo de
Pressão Seletiva é 1, o qual corresponde a situação
na qual todos os indivíduos são iguais (diversidade nula).
![]()
REPRESENTAÇÃO E CODIFICAÇÃO DOS AG’S
As partes que relacionam um AG a um problema dado são a codificação e a função de avaliação.
Se um problema pode ser representado por um conjunto de parâmetros (genes), estes podem ser unidos para formar uma cadeia de valores (cromossomo), este processo se chama codificação. Em genética, este conjunto representado por um cromossomo em particular é referenciado como genótipo, contendo a informação necessária para construir um organismo, conhecido como fenótipo. Estes mesmos termos se aplicam em AG. Por exemplo, para se desenhar um prédio, um conjunto de parâmetros especificando o desenho da planta é o genótipo, e a construção final é o fenótipo. A adaptação de cada indivíduo depende de seu fenótipo, no qual se pode inferir seu genótipo.
Por
exemplo, para um problema de maximizar uma função de três
variáveis, ![]() , se poderia representar
cada variável por um número binário de 10 bits, obtendo-se
um cromossomo de 30 bits de longitude e 3 genes.
, se poderia representar
cada variável por um número binário de 10 bits, obtendo-se
um cromossomo de 30 bits de longitude e 3 genes.
Existem vários aspectos relacionados com a codificação de um problema a serem tomados em conta no momento de sua realização:
Deve ser utilizado um alfabeto o mais pequeno possível para representar os parâmetros; normalmente utilizam-se dígitos binários;
As variáveis que representam os parâmetros do problema devem ser discretizadas para poder representar as strings de bits;
A maior parte dos problemas tratados com AG's são não lineares e muitas vezes existem relações "ocultas" entre as variáveis que formam a solução;
O tratamento dos genótipos inválidos deve ser tomado em conta para o desenho da codificação.
SELEÇÃO DAS FUNÇÕES DE AVALIAÇÃO E APTIDÃO
As funções de avaliação e de aptidão devem ser elaboradas tendo em vista o tipo de problema a ser resolvido, ou seja, para cada problema teremos, na grande maioria dos casos, que criar novas funções para atribuição dos valores de aptidão aos indivíduos componentes da população.
Torna-se necessário diferenciar função de aptidão e função de avaliação para fazer que as avaliações assumam valores positivos e para controlar a densidade da população.
Inicialmente, a função de avaliação se faz coincidir com o objetivo a maximizar, isso sem esquecer que nem sempre é fácil especificar numericamente o objetivo.
Uma vez que a função deve ser de fácil manipulação prática, pode ocorrer, em determinadas circunstâncias, que exista um objetivo claramente definido, mas a determinação explícita de seu valor para cada indivíduo é complicada. Em tal situação, não se pode tomar esse objetivo como função de avaliação, visto que seria inoperante.
Dado que os AG’s maximizam atitudes, se admite por padrão que se maximiza o objetivo. Em certos casos pode ser mais prático determinar o problema como sendo de minimização de certo objetivo.
Uma vez selecionada a função de avaliação, é construída a função de aptidão deslocando-a e escalonando-a convenientemente. Sendo que o deslocamento tem, por finalidade principal, fazer com que a função de aptidão retorne valores positivos, o procedimento mais utilizado para tornar as avaliações positivas é o da janela de deslocamento, o qual consiste em deslocar as avaliações da seguinte forma:
![]()
onde
![]() é um limite superior para
as avaliações, ou seja,
é um limite superior para
as avaliações, ou seja,
![]()
Como
não é habitual conhecer antecipadamente a faixa de valores que
vai ser assumida pela função de aptidão, é preferível
ir adaptando dinamicamente o valor de ![]() da seguinte forma:
da seguinte forma:
![]()
onde
![]() é a aptidão máxima
de qualquer indivíduo avaliado até a iteração imediatamente
anterior,
é a aptidão máxima
de qualquer indivíduo avaliado até a iteração imediatamente
anterior, ![]() .
.
Então,
se o valor de ![]() não está
suficientemente próximo da máxima aptidão da presente geração,
pode ocorrer uma freada na busca e até mesmo uma estagnação.
Isto ocorre devido a perda da diversidade na população pois, se
não está
suficientemente próximo da máxima aptidão da presente geração,
pode ocorrer uma freada na busca e até mesmo uma estagnação.
Isto ocorre devido a perda da diversidade na população pois, se
![]() possui um valor muito superior que
qualquer avaliação atual, as correspondentes aptidões serão
todas muito parecidas, se reduzirá a pressão seletiva em direção
dos melhores indivíduos e a busca estagnará, podendo ocorrer deriva
genética. Para melhor entendimento, suponhamos que o valor de
possui um valor muito superior que
qualquer avaliação atual, as correspondentes aptidões serão
todas muito parecidas, se reduzirá a pressão seletiva em direção
dos melhores indivíduos e a busca estagnará, podendo ocorrer deriva
genética. Para melhor entendimento, suponhamos que o valor de ![]() = 100 e que no presente instante a população só apresenta
indivíduos com valores de avaliação entre 5 e 10. Usando
= 100 e que no presente instante a população só apresenta
indivíduos com valores de avaliação entre 5 e 10. Usando
![]() , teríamos valores
de aptidão variando entre 90 e 95, o que por exemplo, na hora da distribuição
na roleta, não diferenciaria muito os melhores indivíduos. Mas
se
, teríamos valores
de aptidão variando entre 90 e 95, o que por exemplo, na hora da distribuição
na roleta, não diferenciaria muito os melhores indivíduos. Mas
se ![]() = 15, teríamos uma faixa
de aptidões variando entre 5 e 10 o que, segundo a formula usada antes,
nos daria para o indivíduo mais apto um valor que seria o dobro do valor
do menos apto, o que melhoraria o processo de discriminação de
aptidões.
= 15, teríamos uma faixa
de aptidões variando entre 5 e 10 o que, segundo a formula usada antes,
nos daria para o indivíduo mais apto um valor que seria o dobro do valor
do menos apto, o que melhoraria o processo de discriminação de
aptidões.
Pelo
apresentado, nota-se ser conveniente fazer uma atualização periódica
do valor de ![]() visando evitar a perda
da diversidade.
visando evitar a perda
da diversidade.
Uma das formas de controlar a diversidade é o uso de uma função de aptidão diferente da função de avaliação, o que é conhecido como escalonamento da função de avaliação. Com o escalonamento se tenta evitar um fenômeno com causas opostas ao anterior mas que produz efeitos semelhantes: é o fenômeno já comentado da convergência prematura em direção a superindivíduos. Segundo Goldberg [GOL89]:
"desde o estudo pioneiro de De Jong, o escalonamento dos valores da função objetivo tem se tornado uma prática amplamente aceita. Isto tem sido feito para manter os níveis apropriados de competição durante uma simulação. Sem escalonamento, existe a tendência de que uns poucos superindivíduos dominem o processo de seleção. Neste caso, os valores da função objetivo devem ser subescalonados para evitar que tais indivíduos ocupem a população. Mais tarde, quando a população tiver convergido quase em sua totalidade, a competição entre os membros da população é menos intensa e a solução tende a evoluir erráticamente. Em este caso os valores da função objetivo devem ser sobreescalonados para acentuar as diferenças entre os membros da população com o fim de continuar favorecendo os melhores membros."
![]()
Até o momento foi explanado como funcionam os Algoritmos Genéticos, o que, visto de uma forma superficial, leva a pensar que os AG's processam apenas indivíduos, ou seja, elementos codificados de um conjunto de possíveis soluções para determinado problema.
Se esse fosse o caso, não teria grande sentido a utilização da codificação binária pois o AG deveria funcionar com a mesma eficiência com números de ponto flutuante que representassem diretamente as possíveis soluções, tendo apenas que modificar levemente os operadores genéticos. Implementando tal idéia na solução de um problema [RIO92], pode-se notar que o AG resultante também converge, mas de forma muito mais lenta, não sendo mais eficiente que outros métodos de busca cega.
O motivo disto é que os AG's não processam unicamente indivíduos, e sim padrões de semelhança entre ditos indivíduos e, tendo em vista que cada indivíduo pode conter muitos padrões simultaneamente, a eficiência da busca se multiplica.
Nesta parte do trabalho, será explicado "porquê" os AG's funcionam, dando o devido embasamento teórico para tal explicação.
Definições e Conceitos Básicos
Holland não foi apenas pioneiro no uso dos AG’s. Ele também propôs a primeira explicação de como os Algoritmos Genéticos trabalham mediante o teorema dos Esquemas [HOL75]. A fundamentação teórica dos AG’s é geralmente representada em termos de ditos Esquemas, os quais são conjuntos de cromossomos que partilham certas semelhanças na sua composição.
Um Esquema é um padrão de semelhança nas strings que compões os cromossomos de um AG, o qual é implementado incluindo mais um símbolo, o “*”, representando indiferença, no alfabeto utilizado para representação. Desta forma, para codificação binária, o alfabeto passa a ser {0, 1, *}, onde * representa qualquer um dos valores possíveis.
Por exemplo, o Esquema (*10*0011) representa estes quatro cromossomos:
|
01000011
|
||
|
01010011
|
||
|
11000011
|
||
|
11010011
|
Desta forma,
os Esquemas permitem descrever sinteticamente configurações de strings que apresentem
características interessantes para a resolução de um determinado problema. Naturalmente
o Esquema (10011001) representa apenas um cromossomo (não possui o símbolo *),
enquanto que o esquema (********) representa todos
os cromossomos de comprimento ![]() =8.
=8.
Deve-se sempre levar em conta que o * é usado apenas na análise do AG, ou seja, o AG não processa Esquemas. Para podermos formalizar , devemos levar em conta, quanto aos cromossomos compostos por strings binárias, o que segue:
 |
Com isto definido, podemos então definir a notação utilizada para permitir a representação dos Esquemas:
 |
Formalizando
Tendo em foco as noções básicas apresentadas no item anterior, pode-se então verificar as seguintes propriedades relativas aos Esquemas [SER96]:
| Se
um Esquema contém k símbolos de indiferença (*)
então representa a 2 |
|
| Uma
string binária de comprimento |
|
| Considerando
as strings binárias de comprimento
|
|
| Uma
população de n cromossomos de comprimento
|
Dadas tais propriedades, é conveniente definir dois conceitos de grande importância para um dado Esquema H:
|
Ordem de um Esquema, o(H): número de valores fixos na representação de um esquema. Por exemplo: 10*110* é de ordem 5 -----» o(10*110*)=5 0****** é de ordem 1 -----» o(0******)=1
|
|
|
Comprimento definidor de um Esquema, d(H): distância em dígitos entre o primeiro e o último valor fixo na representação do Esquema. Por exemplo: 10*110* tem d(H) 5 -----» d(10*110*) = (6-1) = 5 0****** tem d(H) 0 -----» d(0******) = (1-1) = 0 |
Dado
que um Esquema H representa 2![]() cromossomos,
quanto maior seja a ordem do Esquema, menos indivíduos ele representará. Devemos
notar que um esquema com uma única posição especificada possui uma longitude
característica de 0. Logo, pode-se calcular a probabilidade de sobrevivência
de um esquema em relação aos cruzamentos. Por exemplo, o esquema S = (****00**1*)
possui ordem o(S)=3 e uma longitude característica
cromossomos,
quanto maior seja a ordem do Esquema, menos indivíduos ele representará. Devemos
notar que um esquema com uma única posição especificada possui uma longitude
característica de 0. Logo, pode-se calcular a probabilidade de sobrevivência
de um esquema em relação aos cruzamentos. Por exemplo, o esquema S = (****00**1*)
possui ordem o(S)=3 e uma longitude característica ![]() (S)
=9-5=4.
(S)
=9-5=4.
A aptidão média da população no instante t, AveFitness(P[t]), é a média das aptidões de todas as strings da população no instante t, ou em equivalência, a aptidão do esquema (* . . . *) em P[t]:

A aptidão relativa de S em P[t]:
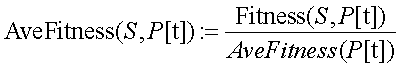
Por fim, sendo Pxov e Pmut as probabilidades de cruzamento e mutação de um AGS respectivamente, a presença de certo esquema S na população P[t] evolui em média de acordo com a equação[CR]:

Assumindo para tal que, como acontece geralmente, Pmut <1.
Teorema Fundamental dos Algoritmos Genéticos
Tendo como base os resultados anteriores, podemos proceder o enunciado do seguinte teorema:
"Nas sucessivas gerações de um AGS, a presença de um esquema S na população P[t] evolui estatisticamente de modo exponencial de acordo com a equação [CR]."
![]()
ALGORITMOS GENÉTICOS PARALELOS
Paralelismo nos Algoritmos Genéticos
Os AG´s são habitualmente considerados algoritmos implicitamente paralelos, sendo esta característica um dos seus pontos fortes. Atualmente existe uma procura cada vez maior por algoritmos que, além de resolver os problemas de forma aceitável, também os resolvam de um modo que seja paralelizável, pois cada vez mais a tendência está voltada para a utilização de sistemas paralelos. Os AG possuem uma estrutura computacional altamente paralelizável. Assim, se analisarmos a estrutura de um AG chegamos às seguintes conclusões:
| Cada cromossomo da população tem uma qualidade Q, que pode ser avaliada independentemente de qualquer outro fator. | |
| Cada operador e operação genética é independente, pelo que podem ser aplicado em qualquer ordem, seqüencial ou não, a qualquer elemento da população. |
Observando mais uma vez a Natureza, chegamos à conclusão que nela todos os processos são paralelos, ou seja, os processos seqüenciais é que não são naturais. Basta imaginarmos que neste momento, em qualquer parte do mundo, existem crianças nascendo, lutas pela sobrevivência, pessoas morrendo, e muitas outras atividades, sem que exista um ponto comum de controle. Podemos interferir diretamente ou não no que se passa, mas não existe ninguém com um conhecimento global do estado atual do mundo e acima de tudo ninguém consegue interferir ou controlar tudo o que acontece.
Modelos de Algoritmos Genéticos Paralelos
Uma das áreas de maior investigação nos AGs tem sido sobre o modo como podem ser efetivamente paralelizados, tendo surgido desse esforço um grande conjunto de possíveis implementações. O que todas estas diferentes implementações têm demonstrado é que o que é importante não é apenas o algoritmo em si, mas sim o conjunto do algoritmo, os problemas para que vai ser utilizado, a sua parametrização e o equipamento que vai servir de base à execução do AG.
Embora estes já fossem fatores essenciais nos algoritmos seqüenciais, o que se veio a notar é que surgiram muitos algoritmos que eram bons em determinadas situações, piores em outras e com pequenas variações de parâmetros e/ou nos problemas tudo se poderia inverter. Foram ainda acrescentados mais fatores a um problema que já não era simples. Assim, poderíamos ter um excelente algoritmo para executar num conjunto de transputers, que se fosse executado numa rede de workstations já não seria tão bom, ou vice-versa, mas dependendo também da parametrização e do problema.
O primeiro modelo que vai ser descrito, é a evolução natural do modelo seqüencial, que embora não seja dos mais eficientes, tem algumas vantagens em algumas utilizações especiais. Serão ainda apresentados dois outros modelos, que ao longo dos últimos anos se têm mostrado especialmente eficazes, que são o modelo Ilha e o modelo da Vizinhança, tendo cada um deles os seus pontos fortes.
Um fator bastante interessante nos AG paralelos, é que é possível que as soluções paralelas sejam, não apenas obtidas mais rapidamente, mas também tenham normalmente uma melhor qualidade que as soluções seqüenciais.
![]() Modelo de Farming
Modelo de Farming
Este modelo (chamado de Farming devido à analogia com uma fazenda em que existem várias tarefas para fazer e várias pessoas paras executá-las, controladas por um capataz), segue uma estrutura do tipo Mestre-Escravos, e é uma evolução quase natural do AG seqüencial. Assim, neste modelo temos um processo Mestre, que supervisiona a população e faz a seleção dos cromossomos em que se vai atuar. A partir da altura em que é feita a seleção, entrega o trabalho a um dos N processos Escravos, que executarão os operadores genéticos, avaliarão os cromossomos gerados e depois devolvem os cromossomos ao processo Mestre, enquanto este já entregou mais trabalho a outros Escravos.
Tem o inconveniente de ser necessário centralizar a seleção, e obrigar a comunicar os parâmetros para os Escravos atuarem e depois os resultados para o Mestre. No entanto, em sistemas que esta comunicação seja feita muito rapidamente, como em sistemas de memória partilhada, é uma solução bastante aceitável. Tem ainda problemas de escalabilidade, pelo que o seu uso obriga a calcular com rigor a quantidade de processos Escravos que será razoável ter, de modo que o processo Mestre possa funcionar sem sobrecarga.
![]() Modelo Ilha
Modelo Ilha
Observação de ambientes naturais isolados, como as ilhas, têm demonstrado que algumas das espécies que surgem são especialmente adaptadas às particularidades dos seus ambientes, em contraste com Populações equivalentes mas em ambientes mais abertos, em que todos os membros têm acesso a todos os outros membros.
Estas observações levaram ao surgimento de novas arquiteturas e operadores que melhoravam os AGs paralelos para além do ganho puro de performance, que em conjunto com as considerações relativas à possibilidade de varias populações concorrentes poderem gerar uma melhor solução do que a conseguida com apenas uma população, levaram à construção de um modelo que aproveita ambas as vantagens. Aproveita os ganhos de fiabilidade na obtenção de soluções com a melhor qualidade das soluções.
Este modelo é o chamado modelo Ilha, devido à fonte inspiradora do conceito. Assim, o algoritmo seqüencial fica dividido numa série de Ilhas (populações), que comunicam entre si as melhores soluções. No resto do tempo, estão trabalhando para melhorar as soluções internas da ilha. Este modelo, entretanto, mantém a estrutura seqüencial do AG, apenas sendo adicionados os operadores para fazer a migração dos elementos entre as diferentes ilhas, não existindo um verdadeiro paralelismo no algoritmo.
![]() Modelo da Vizinhança (Difusão)
Modelo da Vizinhança (Difusão)
Consiste em dividir todo o AG, de modo a conseguir levar mais longe o paralelismo. Para tal, é feita a mesma divisão da população pelos vários processadores, mas em vez de usar o conceito de ilha para se fazer a migração, estabelece-se uma vizinhança com a qual é feito o normal processo de seleção e reprodução.
Este é o modelo da Vizinhança (East [EAS93], M. Gorges-Schleuter [SCL90]), também conhecido por modelo de Difusão, pois os bons cromossomos vão-se difundindo gradualmente pelos vários processadores. Como exemplo, se tivermos uma população de 100 elementos, podemos imaginar uma grade de 10x10 e dizer que cada uma das células tem uma vizinhança, a qual por questões de velocidade, seria composta pelos elementos imediatamente à sua volta na arquitetura usada. Esta vizinhança vai ser usada para selecionar quais dos cromossomos vão ser usados para gerar o novo cromossomo.
Depois é necessário substituir o cromossomo atual pelo cromossomo que acabou de se gerar. Esta fase de substituição é bastante crítica, pois se o elemento for substituído por um elemento com pior qualidade o algoritmo sai muito afetado.
Este algoritmo, tal como o modelo Ilha, também pode ser visto na Natureza, pois é uma aproximação daquilo que acontece quando aumentamos o tamanho de uma Ilha. Imagine que a evolução dos animais numa ilha é relativamente independente da evolução dos animais nas ilhas vizinhas, sendo ocasionalmente feita a emigração de alguns animais. Como vimos, este modelo funciona bem, e tem a vantagem de em cada Ilha poderem aparecer animais mais adaptados à ilha em questão. Agora, suponha que em vez de uma ilha pequena, em que cada elemento da população pode comunicar com qualquer outro, passamos para uma situação em que a ilha é tão grande que se torna impossível a comunicação entre todos os elementos da população. Aí o que aparece é a criação de nichos de população, como as aldeias, em que cada elemento tem maior probabilidade de encontrar o seu par na sua aldeia, mas uma probabilidade menor de encontrá-lo numa aldeia próxima e uma probabilidade ainda menor de encontrar o par numa aldeia longínqua.
Este modelo além de ter as mesmas vantagens do modelo da Ilha, tem também a seu favor o fato de ser massivamente paralelizável, pois as operações a nível de cada célula são muito simples, além de que não é necessária comunicação a grandes distâncias. Embora este seja o modelo que parece ter mais facilidade de escalar para grande número de processadores, tem no entanto o problema de ser de grão muito fino. Em cada processador apenas fica um cromossomo, sendo os cromossomos vizinhos transmitidos para o processador atual para a seleção e reprodução. Caso se opte por passar este modelo para um grão médio, acumulando vários cromossomos em cada processador, podemos optar por fazer o escalonamento de vários processos por processador, cada um atendendo a um cromossomo ou podemos elaborar um algoritmo seqüencial em cada nodo, que atenda a cada um dos pontos da grade que controla.
Toda a estrutura deste algoritmo assenta num grande grau de comunicação entre as várias partes da população, quer seja com um cromossomo por processador quer sejam vários cromossomos por processador. No caso de estar sendo utilizado um sistema cujas comunicações sejam muito rápidas, este modelo obtém performances equivalentes ao modelo da ilha. No entanto, não é adequado a sistemas com comunicações mais lentas, como através de uma rede Ethernet.
![]()
Nesta parte do texto, será traçado um breve paralelo entre a terminologia biologica (BIO) - [ABE70], [EVO98] - e a terminologia da Computação Evolutiva (CE) - [SCH98], [EVO98] - dos principais termos empregados neste trabalho, visando auxiliar no entendimento dos conceitos aplicados: ·
|
(BIO) ADAPTABILIDADE: Toda característica de um organismo vivo que aumenta as possibilidades de sobrevivência e de deixar descendência no meio em que habita. Também proporcional ao tempo esperado para extinção. "Os adaptados são aqueles que se ajustaram ao Ambiente existente ao seu redor e cujos descendentes se ajustarão a ambientes futuros." (J. Thoday, - UM Século de Darwin, 1959). (CE) Qualquer alteração na estrutura de um cromossomo (string de caracteres de certo alfabeto) que melhore sua capacidade de resolver determinado problema, permitindo-lhe maiores chances de sobrevivência e reprodução. · |
|
|
(BIO) AJUSTE : Medida que indica o grau de aptidão de um indivíduo ao meio ambiente. (CE) Valor de Adaptabilidade ou Fitness. Valor relativo a avaliação da Função Objetivo de uma solução. Também chamada de função de Avaliação ou Função Objetivo em problemas de otimização. · |
|
|
(BIO) ALELOS : Se diz que dois ou mais GENES são ALELOS (entre si) ou ALELOMORFOS (um em relação ao outro), quando: 1. Ocupam a mesma posição relativa (LOCUS) em CROMOSSOMOS HOMÓLOGOS e quando, na mesma célula se unem em pares durante a meiose; 2. Produzem efeitos diferentes no mesmo grupo de processos do desenvolvimento; 3. Podem mutar de um para o outro. (CE) Possíveis valores dos genes (no caso de representação binária 0 ou 1). · |
|
|
(BIO) CROMOSSOMO : Corpo em forma de filamento, constituído principalmente por DNA e proteína, que se encontra em número variável no núcleo de todas as células animais e vegetais. Componente genético responsável pelo fenótipo do indivíduo. (CE) Um vetor ou string devidamente codificado, pertencente ao conjunto de possíveis soluções de um determinado problema. · |
|
|
(BIO) DIPLOIDE: Diz-se do núcleo cujos cromossomos se apresentam aos pares, sendo homólogos (contém os mesmos GENES na mesma seqüência) os membros de cada par, de forma que há um número o dobro do número haploide. (CE) Em cada local do cromossomo existe um par de genes. Isto permite uma boa economia de memória. · |
|
|
(BIO) ESPÉCIE : Grupo de indivíduos intercruzantes que são isolados reprodutivamente de outros grupos semelhantes, contendo fenótipos semelhantes. (CE) Indivíduos componentes de uma mesma população. · |
|
|
(BIO) FENÓTIPO : Conjunto das características de um indivíduo observadas ou discerníveis por outros métodos, fornecidas pelo genótipo. (CE) Expressão física das estruturas. Conjunto decodificado de parâmetros. · |
|
|
(BIO) GENES : Unidade de material hereditário. Unidade básica do cromossomo que define, de acordo com seu valor e posição, uma característica; um determinador hereditário que especifica uma função biológica; uma unidade de herança (DNA) localizada em um lugar fixo no cromossomo. (CE) Variáveis componentes da string que representa o cromossomo. · |
|
|
(BIO) GENÓTIPO : Arranjo dos genes e cromossomos de um organismo correspondente a determinado fenótipo. (CE) Estruturas atuais. Cromossomos codificados. · |
|
|
(BIO) HAPLOIDE: Célula que contém um único CROMOSSOMO ou conjunto de CROMOSSOMOS em vez de dois em cada núcleo, cada qual consistindo de uma única seqüência de GENES. Um exemplo é um GAMETA. (CE) Em lugar de um cromossomo existe um AG Modelo Ilha de um gene simples. · |
|
|
(BIO) INDIVÍDUO : Um exemplar de uma espécie que interage com o meio ambiente. (CE) Mesmo que Cromossomo. · |
|
|
(BIO) MUTAÇÃO : Variação devida a alguma alteração da constituição hereditária com aparecimento de uma nova variedade em qualquer espécie viva. (CE) Modificação aleatória do cromossomo visando gerar novas possíveis soluções à explorar. · |
|
|
(BIO) POPULAÇÃO : Conjunto de indivíduos da mesma espécie; grupos inteiros de organismos de um tipo; um grupo intercruzante de animais ou vegetais; grupo amplo do qual pode-se tomar uma amostra. (CE) Conjunto de possíveis soluções. · |
|
|
(BIO) REPRODUÇÃO : Multiplicação de novos indivíduos a partir de outros de mesma espécie. (CE) Cruzamento (crossover) vem a ser uma troca de segmentos dos cromossomos (strings) selecionados. · |
|
|
(BIO) SELEÇÃO NATURAL : Mecanismo que garante aos indivíduos mais aptos, maiores chances de reprodução; fertilidade diferencial na natureza que favorece indivíduos que se adaptam melhor ao meio ambiente e tende a eliminar aqueles não adaptados. (CE) Determinada pela aptidão (fitness) do indivíduo. Quanto maior a sua aptidão, maiores as chances de gerar descendentes. Indivíduos com aptidões baixas representam soluções indesejáveis no momento da avaliação. |
![]()
[ABE70] ABERCROMBIE, M., C. J. Hickman e M. L. johnson. Diccionario de Biología. Barcelona: Editorial Labor S. A., 1970.
[BAC96] BÄCK, Thomas. Evolutionary Algorithms in Theory and Practice: Evolution Strategies, Evolutionary Programming, Genetic Algorithms. New York:Oxford University Press, 1996.
[BEA93a] BEASLEY, David, David R. Bull e Ralph R. Martin. An Overview of Genetic Algorithms: Part 1, Fundamentals. - Technical Report - Cardiff /UK:Department of Computing Mathematics - University of Wales College of Cardiff, 1993.
[BEA93b] BEASLEY, David, David R. Bull e Ralph R. Martin. An Overview of Genetic Algorithms: Part 2, Research Topics. - Technical Report - Cardiff /UK:Department of Computing Mathematics - University of Wales College of Cardiff, 1993.
[DAV91] DAVIS, Laurence. Handbook of Genetics Algorithms. New York:Van Nostraud Reinhold, 1991.
[DEJ75] DEJONG, K. A. An Analysis of the Behavior of a Class of Genetic Adaptative Systems. - Doctoral dissertation - University of Michigan, 1975.
[DOR93] DORIGO, M. and MANIEZZO, V. Parallel genetic algorithms: Introduction and overview of current research. In J. Stender, editor, Parallel Genetic Algorithms: Theory and Applications. IO Press,Washington DC, 1993.
[EAS93] EAST, I. and MACFARLANE, D., Implementation in Occam of Parallel Genetic Algorithms on Transputer Networks, J. Stender: Parallel Genetic Algorithms, IOS Press 1993
[EVO98] Hitch Hiker's Guide to Evolutionary Computation, Issue 6.3, released 30 September 1998 http://www.cs.purdue.edu/coast/archive/clife/ FAQ/www/Q99_1.htm
[GOL89] GOLDBERG, David E. Genetic Algorithms in Search, Optimization and Machine Learning. Massachusets: Addison-Wesley Co, 1989.
[GRE90] GREFENSTETTE, John j. A User's Guide to GENESIS. 1990.
[HOL75] HOLLAND, John H. Adaptation in Natural and Artificial Systems. Ann Arbor:University of Michigan Press, 1975.
[MIC96] MICHALEWICZ, Z. Genetic Algorithms + Data Structures = Evolution Programs. New York: Springer-Verlag Berlin Heidelberg, 1996.
[MIT96] MITCHELL, Melanie. An Introduction to Genetic Algorithms. Massachusets: MIT Press, 1996.
[OLI95] OLIVEIRA, Vitor Serafim Pereira de. Arquiteturas Paralelas. - Relatório Técnico - Braga: Universidade do Minho, 1995.
[PAL97] PALAZZO, Luiz A. M. Algoritmos para Computação Evolutiva. - Relatório Tecnico - Pelotas: Grupo de Pesquisa em Inteligência Artificial - Universidade Católica de Pelotas.
[RIC93] RICH, Elaine e Kevin Knight. Inteligência Artificial 2ª Ed. São Paulo:Makron Books do Brasil Editora Ltda, 1994.
[RIO92] RIOLO, Rick L. Los Bits Mejor Dotados. Investigación y Ciencia, setembro de 1992.
[SCH98] SCHNEIDER, André M. Algoritmo Adaptativo Genético para Acompanhamento da Trajetória de Alvos Móveis. - Dissertação de Mestrado - Porto Alegre:Instituto de Informática - Universidade Federal do rio Grande do Sul, 1998.
[SCL90] SCHLEUTER, M. Gorges-,Explicit Parallelism of Genetic Algorithms through Population Structures, -Parallel Problem Solving from Nature (PPSN1), Proceedings, 1990.
[SER96] SERRADA, Anselmo P. Una Introducción a la Computación Evolutiva, 1996.
[YEP99] YEPES, Igor. Algoritmo Genético com Idades para Controle de Braço Mecânico. Erechim/RS: URI - Universidade Regional Integrada, 1999.
[YEP00] YEPES, Igor. Algoritmos Genéticos Paralelos. Trabalho Individual - Porto Alegre/RS: UFRGS - Universidade Federal do Rio rande do Sul, 2000.
Página Principal
Noções Básicas
Algoritmos Genéticos
Redes Neurais Multiagentes
Cognição Software
Artigos Tutoriais
Links Quem
sou eu