Definizione di 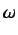$\omega$ e $\psi$

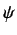
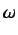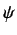Per la i-esima caratteristica di una determinata categoria (si riguardino le equazioni(3.5) e (3.6) ), $\omega$ e $\psi$ combinano i parametri 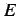$E$ e $P$ alla seguente maniera:

$${\large \mu_{i} = \omega \left( \{ E_i , P_i \} \right) = P_i }$$ (3.19)

$${\large \sigma_{i}^{2} = \psi \left( \{ E_i , P_i \} \right) = E_i \cdot P_i }$$ (3.20)

se si sostituiscono le due equazioni nella (3.4), si ottiene la i-esima funziona Gaussiana, relativa alla i-esima caratteristica:

$$g_i(x_i,\{ E_i, P_i \}) = \exp \left( - \frac{(x_i - P_i)^2}{2 \cdot E_i \cdot P_i} \right)$$ (3.21)

Il valore medio della Gaussiana definito nella equazione (3.19) può assumere solo valori nell'intervallo $(0,1]$, in quanto la Presenza $P$ di un termine in una categoria può essere quasi $0$ se la parola appare raramente nei documenti di quella categoria, o può essere prossima a $1$ se appare in ogni documento di essa. La varianza della Gaussiana, vista nella equazione (3.20), è anche essa chiaramente compresa nell'intervallo $(0,1]$.

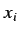Quando $x_i$ è fissato (si vedrà nella prossima sezione come) si può comparare l'output di due o più differenti funzioni gaussiane.

La Figura 3.3 mostra un esempio di due parole di due differenti categorie, una con $P = 0.5$ e $E = 0.5$, l' altra con $P = 0.5$ e $E = 0.9$. Il termine con la più alta espressività è quello che ha l' output più alto della funzione gaussiana.

Figura 3.3: esempio di due $g_i$ con valori di $P_i$ uguali ma $E_i$ differenti. A parità di $P$, più alta è l' espressività di un termine, più alto è l' ouput della gaussiana.